Null-Wissen-Beweis

Ein Null-Wissen-Beweis kann mit hoher Wahrscheinlichkeit nachweisen, dass man ein Geheimnis weiß, ohne das Geheimnis zu verraten. Dieser Nachweis passiert meist nach einem Frage-Antwort-Protokoll und hat viele Anwendungen in der Kryptografie. Eine Partei versucht zu beweisen, die andere Partei verifiziert. Der Beweiser überzeugt dabei den Verifizierer mit einer gewissen Wahrscheinlichkeit davon, dass er ein Geheimnis kennt, ohne dabei Informationen über das Geheimnis selbst bekannt zu geben. Ein bekanntes Verfahren ist das Feige-Fiat-Shamir-Protokoll. Die Schnorr-Identifikation erfordert nur drei Schritte zur Kommunikation und der Beweiser kann den Verifizierer nur mit minimaler Wahrscheinlichkeit davon überzeugen, ein Geheimnis zu kennen, das er nicht kennt.

Der Null-Wissen-Beweis heißt auch kenntnisfreier Beweis, kenntnisfreies Protokoll, Zero-Knowledge-Proof oder Zero-Knowledge-Protocol.

Anwendungen

Zero-Knowledge-Protokolle dienen u. a. der Authentifizierung. Bei einigen Kryptowährungen wie Zcash oder mobilen Zahlungsdiensten wie Bluecode erhöhen sie die Anonymität des Zahlungsverkehrs.

Eigenschaften

In der Praxis werden sie zur Authentifizierung jedoch kaum verwendet, da sie in der Regel für ein ausreichendes Sicherheitsniveau ein hohes Maß an Interaktion, d. h. den Austausch vieler Nachrichten, erfordern und anfällig für Replay-Angriffe sind. Die in praktischen Anwendungen eingesetzten und standardisierten Authentifizierungsprotokolle basieren stattdessen auf digitalen Signaturen. Allerdings gibt es auch Konstruktionen, welche bestimmte Zero-Knowledge Protokolle in nicht-interaktive Varianten überführen.

Zero-Knowledge-Protokolle stellen eine Erweiterung von interaktiven Beweissystemen dar. Zu den Bedingungen Vollständigkeit und Zuverlässigkeit der interaktiven Beweissysteme tritt noch die Zero-Knowledge-Eigenschaft, die dafür sorgt, dass der Verifizierer keine Information über das Geheimnis erlangt.

Bei einem Zero-Knowledge-Protokoll soll immer gezeigt werden, dass eine Eingabe $x$ einer formalen Sprache $L$ angehört. Dazu muss ein Zero-Knowledge-Protokoll drei Bedingungen erfüllen:

Vollständigkeit

Ist die Eingabe $x$ ein Element der Sprache $L$, dann soll ein Verifizierer nach Ablauf des Protokolls fast immer akzeptieren.

Zuverlässigkeit

Ist die Eingabe $x$ kein Element der Sprache $L$, also der Beweiser unehrlich, dann soll der Verifizierer nach Ablauf des Protokolls ablehnen. Dabei ist jedoch eine geringe Fehlerwahrscheinlichkeit erlaubt.

Zero-Knowledge-Eigenschaft

Aus der Interaktion zwischen dem Beweiser und dem Verifizierer darf nicht mehr Wissen als die (Un-)Gültigkeit der zu beweisenden Aussage gewonnen werden. Ein Dritter, der die Interaktion zwischen Beweiser und Verifizierer verfolgt, erfährt nicht einmal, ob der Beweiser überhaupt das Geheimnis kennt (oder die Interaktion zwischen B und V abgesprochen war).

Klassisches Beispiel

Das nachfolgende anschauliche Beispiel für ein Zero-Knowledge-Protokoll wurde von Jean-Jacques Quisquater et al. (s. Literatur) entworfen.

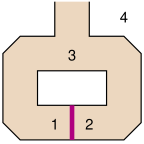
Peggy möchte Viktor beweisen, dass sie ein Geheimnis kennt – wie man die Tür in einer Höhle öffnen kann –, ohne dass sie die Tür vor seinen Augen öffnet und dabei das Geheimnis verrät. Zudem will Peggy ausschließlich Viktor davon überzeugen, dass sie das Geheimnis kennt, und nicht Dritte.

Zunächst steht Viktor bei 4 und sieht Peggy in die Höhle gehen, aber nicht, ob Peggy den Weg 1 oder 2 nimmt. Dann geht Viktor zu 3 und verlangt von Peggy, dass sie auf einem bestimmten Weg aus der Höhle kommt. Wenn Peggy nicht auf der richtigen Seite steht, muss sie dafür die rote Tür öffnen.

Nur wenn Peggy die Tür öffnen kann, kann sie jedes Mal auf der von Viktor verlangten Seite herauskommen. Kann sie die Tür nicht öffnen, muss sie in 50 % der Fälle auf der falschen Seite zurückkommen.

Kommt Peggy bei n Versuchen (die Tür muss natürlich jedes Mal zuerst wieder verschlossen werden) immer auf der von Viktor verlangten Seite aus der Höhle, kann Viktor mit einer Wahrscheinlichkeit von $1-2^{-n}$ davon ausgehen, dass Peggy das Geheimnis der Tür kennt, hat aber dennoch kein neues Wissen über die Tür erlangt, etwa wie genau sie zu öffnen ist.

Dieser Beweis funktioniert allerdings nur gegenüber Viktor: Beobachtet ein Dritter den Vorgang, ist er nicht davon überzeugt, dass Peggy das Geheimnis der Tür kennt, da sich Viktor und Peggy abgesprochen haben könnten, welche Seite Viktor in jedem der Durchgänge verlangen wird, und Peggy dann immer gleich auf der richtigen Seite in die Höhle gegangen sein könnte.

Peggy könnte Viktor auch direkt beweisen, dass sie das Geheimnis kennt ohne es offenlegen zu müssen: Viktor und Peggy gehen beide zu 3, von wo aus Viktor sieht wie Peggy in eine Richtung in die Höhle geht und auf der anderen Seite herauskommt. Um dies tun zu können, muss sie durch die rote Tür gehen. Viktor sieht von 3 aus zwar nicht, wie das geschieht, und erfährt damit nicht das Geheimnis, weiß aber dennoch sicher, dass Peggy die Tür öffnen kann. Das Problem bei diesem Ansatz ist, dass diese Vorgehensweise aufgezeichnet oder von einer dritten Partei beobachtet werden könnte. Damit kann Peggy nicht mehr abstreiten, das Geheimnis zu kennen, indem sie behauptet, mit Viktor zusammengearbeitet zu haben, und kann somit nicht mehr bestimmen, wer davon erfährt, dass sie das Geheimnis der roten Tür kennt.

Beispiel für ein Zero-Knowledge-Protokoll

Datei:Zero knowledge isograph.png

Ein Zero-Knowledge-Protokoll mit ISOGRAPH

Eine Zero-Knowledge-Authentifizierung zwischen zwei Instanzen kann mit Hilfe des Graphenisomorphieproblems stattfinden. $B$ möchte $V$ letztlich beweisen, das „Geheimnis“ $\pi$ zu kennen. Dies ist naheliegend wenn $B$ plausibel machen kann die Entscheidung $a$ zu kennen (und daher immer richtige Antworten geben zu können). Dazu muss vom Beweiser zunächst einmalig ein öffentliches Schlüsselpaar erstellt werden:

• Der Beweiser $B$ erzeugt einen sehr großen Graphen $G_{0}$.
• $B$ nummeriert $G_{0}$ mit einer zufällig und gleichförmig gewählten Permutationsfunktion $\pi$ um. Der resultierende Graph sei also $G_{1}:=\pi (G_{0})$.
• Das Paar $(G_{0},G_{1})$ wird veröffentlicht, die Permutation $\pi$ hält $B$ geheim.

Angenommen, eine Person, genannt „Verifizierer“, möchte die Identität von $B$ überprüfen, d. h. feststellen, ob $B$ tatsächlich im Besitz des zum öffentlichen Schlüssel $(G_{0},G_{1})$ gehörigen privaten Schlüssels $\pi$ ist. Dann kann $B$ diese Tatsache mit Hilfe des nachfolgenden Zero-Knowledge-Protokolls beweisen, ohne dem Verifizierer oder einer dritten Person den privaten Schlüssel $\pi$ mitzuteilen:

1. Der Beweiser $B$ wählt zufällig ein $a\in \{0,1\}$. Außerdem wird der Graph $G_{a}$ durch die zufällig gewählte Permutationsfunktion $\rho$ umnummeriert. Der resultierende Graph sei $H:=\rho (G_{a})$. $B$ sendet schließlich $H$ an den Verifizierer $V$. In diesem Schritt legt sich der Beweiser also auf einen der Graphen fest (Commitment bzw. Witness).
2. Der Verifizierer $V$ empfängt den Graphen $H$ und wählt zufällig ein $b\in \{0,1\}$. Dann fordert er $B$ auf, ihm eine Permutation $\sigma$ mit der Eigenschaft $H=\sigma (G_{b})$ zu senden (Challenge).
3. Nun muss zwischen drei Fällen unterschieden werden:

   $\sigma :={\begin{cases}\rho &{\text{falls }}a=b\\\rho \circ \pi ^{-1}&{\text{falls }}a=0{\text{ und }}b=1\\\rho \circ \pi &{\text{falls }}a=1{\text{ und }}b=0\end{cases}}$

   $B$ schickt die entsprechend konstruierte Permutation $\sigma$ an $V$ zurück (Response).

4. $V$ empfängt das von $B$ gesendete $\sigma$ und prüft, ob wirklich $H=\sigma (G_{b})$ gilt.

Wir betrachten nun die drei notwendigen Bedingungen für ein Zero-Knowledge Protokoll:

• Das obige Protokoll ist offensichtlich vollständig, weil $\sigma$ gerade so konstruiert wird, dass es die geforderte Gleichung $H=\sigma (G_{b})$ erfüllt.
• Ein unehrlicher Beweiser bzw. eine dritte Person, die sich als $B$ ausgeben möchte, kann ohne Kenntnis von $\pi$ den Verifizierer nur mit einer Wahrscheinlichkeit von 0,5 (durch richtiges Raten des Wertes $a$ im ersten Schritt) überzeugen. Falls das Protokoll hinreichend oft wiederholt wird und unter der Annahme, dass die Bestimmung von $\pi$ aus $(G_{0},G_{1})$ schwer ist, ist das Protokoll also zuverlässig.
• Die Kommunikation zwischen Beweiser und Verifizierer in einer Runde (Schritt 1 bis 4) ist von der Form $(H,b,\sigma )$. Erzeugt nun ein Simulator $S$ zufällig und gleichförmig $b'$ und $\sigma '$ und berechnet damit den Graphen $H'=\sigma '(G_{b'})$, dann ist die resultierende Wahrscheinlichkeitsverteilung $\{(H',b',\sigma ')\}$ identisch mit der Verteilung, welche durch die echten Protokollinstanzen impliziert wird. Folglich kann kein geheimes Wissen (hier die Permutation $\pi$) übertragen worden sein (Zero-Knowledge).

„Zero Knowledge“ als Werbebegriff

Angelehnt an den Zero-Knowledge-Beweis wird von einigen Anbietern von Cloud Computing der Begriff Zero Knowledge benutzt, um deutlich zu machen, dass die Anbieter keinen Einblick in die gespeicherten Dateien der Nutzer haben.

Da der Begriff „Zero Knowledge“ aber bereits ein etablierter Begriff im Bereich Kryptographie und IT-Security ist, haben einige Cloud-Anbieter, die bisher ihre Dienste mit „Zero Knowledge Cloud“ beworben haben, sich dazu entschieden, diesen Begriff nicht mehr zu verwenden.

Literatur

• Jean-Jacques Quisquater, Louis Guillou: How to explain zero-knowledge protocols to your children. Advances in Cryptology - CRYPTO '89, Lecture Notes in Computer Science 435, pp. 628–631, 1990. (PDF)

  Kommentar: Äußerst unterhaltsame und theoriearme Einführung anhand eines mittlerweile klassischen Beispiels.

• Ivan Damgard, Jesper Buus Nielsen: Commitment Schemes and Zero-Knowledge Protocols, 2008, PDF
• Albrecht Beutelspacher, Jörg Schwenk, Klaus-Dieter Wolfenstetter: Moderne Verfahren der Kryptographie, 7. Auflage, S. 43ff, 2010, ISBN 978-3-8348-1228-5

Weblinks

• Applied Kid Cryptography – Eine anschauliche Darstellung eines Zero-Knowledge-Protokolls anhand eines Spiels (englisch)
• Zero-Knowledge Tutorial – Einführung von Oded Goldreich (englisch)