Passung

aus Wikipedia, der freien Enzyklopädie
Verschiedene Passungsarten

Als Passung wird im Maschinenbau die maßliche Beziehung zwischen zwei Teilen bezeichnet, die ohne Nacharbeit zusammenpassen sollen. Meistens haben diese Teile an der Fügestelle dieselbe Kontur, einmal als Innenform, einmal als Außenform.

Typisches Beispiel ist die Welle in einer Bohrung. Der Durchmesser beider Konturen wird als mit einer Toleranz versehenes Maß angegeben. Beide Konturen haben das gleiche Nennmaß. Unterschiedlich sind die beiden Toleranzfelder, innerhalb derer das jeweilige bei der Fertigung entstehende Istmaß von Bohrung und Welle liegen muss.

Es ergibt sich am fertigen Bauteil entweder eine Spielpassung oder eine Übermaßpassung (Presspassung). Sofern die Toleranzen sowohl ein Spiel als auch ein Übermaß ermöglichen, spricht man von einer Übergangspassung, die je nach den erreichten Istmaßen in eine der erstgenannten Gruppen fällt.

Geschichte

Schon vor 1914 hatten mehrere Firmen Passsysteme für eigene Zwecke entwickelt. Nach dem Ersten Weltkrieg wurde daraus das System der DIN-Passungen entwickelt. Die 1926 gegründete International Federation of the National Standardizing Associations (ISA) vereinheitlichte 1928 die Passsysteme verschiedener Nationen. Die ISA-Passungen lösten daraufhin die DIN-Passungen ab. Seit 1964 heißt die Organisation Internationale Organisation für Normung und die Normen ISO 286-1 und 286-2 für Rund- und Flachpassungen gingen unverändert als DIN-Normen ins Deutsche Normenwerk über.

Normung

Passungen sind genormt. Die zuständige Norm ist die ISO-Norm ISO 286. Sie besteht aus zwei Teilen und wurde 1988 ausgegeben. Grundbegriffe von Toleranzen und Passungen regelt ISO 286-1 (aktuelle Neuausgabe 4.2010); ISO 286-2 enthält die Tabellen der Grundtoleranzgrade und Grenzabmaße für Bohrungen und Wellen. Die Norm ist in Deutschland als DIN-Norm veröffentlicht.

Kennzeichnung von Passungen

Bei Passungsangaben in technischen Zeichnungen werden Innenmaße (z. B. Durchmesser einer Bohrung) und Außenmaße (z. B. Durchmesser einer Welle) getrennt betrachtet. Die Passungsangaben können dabei in Form der Angabe von oberen und unteren Abmaßen oder durch Toleranzkurzzeichen geschehen.

Toleranzkurzzeichen

Toleranzkurzzeichen in technischen Zeichnungen sind nach DIN genormt. Die entsprechende Norm ist die DIN 406, die sich mit Maßeintragungen beschäftigt.

Die Passungsangabe selbst besteht immer aus einem oder zwei Buchstaben und einer Zahl. Der bzw. die Buchstaben gibt die Lage des Toleranzfeldes zum Nennmaß, die Toleranzlage, an. Die Zahl kennzeichnet die Größe des Toleranzfeldes, den Toleranzgrad. Siehe dazu: Toleranz (Passungsangaben nach ISO). Zur Darstellung der Toleranzen von Innenmaßen (Bohrung) werden Großbuchstaben und für Außenmaße (Welle) Kleinbuchstaben verwendet.

Merkhilfe: Die Welle muss in die Bohrung passen. Demnach muss die Welle etwas kleiner (⇒ Kleinbuchstaben) und die Bohrung etwas größer (⇒ Großbuchstaben) sein.

Toleranzlage

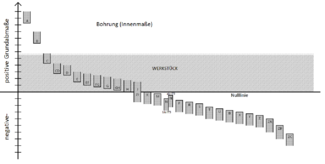
Schematisches Toleranzlagenfeld für Bohrungen im gleichen Nennmaßbereich

Mit den Buchstaben A–ZC wird dabei die Lage des Toleranzfelds zur Nulllinie (Nennmaß), die sogenannte Toleranzlage angegeben. Mit aufsteigendem Buchstaben verschiebt sich die Lage des Toleranzfeldes in Richtung größerer Außenmaße der Wellen bzw. kleinerer Innenmaße der Bohrungen. Bleibt das Gegenstück jeweils unverändert, so verschiebt sich die resultierende Passung mit aufsteigendem Buchstaben in Richtung engerer Passungen.

Beispiele für ein Außenmaß einer Welle:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varnothing 10_{\text{h6}} = \varnothing 10^{0}_{-9} }

Mindestmaß: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 10 \,\mathrm{mm} - 9 \,\text{µm} = 9{,}991 \ \mathrm{mm}}
Höchstmaß: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 10 \,\mathrm{mm} + 0 \,\text{µm} = 10{,}000 \ \mathrm{mm}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varnothing 10_{\text{p6}} = \varnothing 10^{+24}_{+15} }

Mindestmaß:
Höchstmaß: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 10 \,\mathrm{mm} + 24 \,\text{µm}= 10{,}024 \ \mathrm{mm}}

Beispiele für ein Innenmaß einer Bohrung:

Mindestmaß: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 10 \,\mathrm{mm}- 0 \,\text{µm} = 10{,}000 \,\mathrm{mm}}
Höchstmaß: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 10 \,\mathrm{mm} + 36 \,\text{µm}= 10{,}036 \,\mathrm{mm}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varnothing 10^{\text{P9}} = \varnothing 10^{-15}_{-51} }

Mindestmaß: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 10 \,\mathrm{mm}- 51 \,\text{µm}= 9{,}949 \,\mathrm{mm}}
Höchstmaß: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 10 \,\mathrm{mm}- 15 \,\text{µm}= 9{,}985 \,\mathrm{mm}}

H-Passungen liegen direkt über der Nulllinie, im Gegensatz dazu liegen h-Passungen direkt unter der Nulllinie. Die Größe des Toleranzfeldes ist unabhängig von der gewählten Toleranzlage.

Toleranzgrad

[[Hilfe:Cache|Fehler beim Thumbnail-Erstellen]]:
Größe der Toleranzfelder für die Grundtoleranzgrade IT 4 bis IT 10 im Nennmaßbereich von 80 bis 120 mm

Der Toleranzgrad wird durch Zahlen von 1 bis 18 (früher Qualitäten genannt) angegeben. Mit steigender Zahl wächst die Größe des Toleranzfeldes. Weiterhin ist die Größe der Toleranz abhängig vom Nennmaß. Bei kleinen Nennmaßen ist die Toleranz prozentual größer als bei großen Nennmaßen.

Die Zahl gibt die Größe des Toleranzfeldes nach den ISO-Grundtoleranzen (IT01, IT 0, IT1, IT2, …, IT18) an (IT = ISO-Toleranz), mit aufsteigender Zahl vergrößert sich das Toleranzfeld. Die dem Toleranzgrad zugeordnete Zahl ist somit das Kennzeichen für die Qualität bzw. Genauigkeit des Passungselementes.

Beispiele für ein Innenmaß:

Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle \varnothing 10^{\text{D9}}=\varnothing 10_{+40}^{+76}}

Mindestmaß: 10 mm + 40 µm = 10,040 mm
Höchstmaß: 10 mm + 76 µm = 10,076 mm

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varnothing 10^{\text{D11}} = \varnothing 10^{+130}_{+40} }

Mindestmaß: 10 mm + 40 µm = 10,040 mm
Höchstmaß: 10 mm + 130 µm = 10,130 mm

Das Mindestmaß bei Innenmaßen und das Höchstmaß bei Außenmaßen ist unabhängig vom gewählten Toleranzgrad.

Nennmaße und Toleranzeinheit i

Für Nennmaße größer 3 mm bis 500 mm sind die Werte der Toleranzgrade größer oder gleich 5 als Vielfaches der Toleranzeinheit i festgelegt.

Die Toleranzeinheit i ergibt sich rechnerisch zu:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle i = 0{,}45 \cdot \sqrt[3]{D} + 0{,}001 \cdot D}

i in µm (Mikrometer); D in mm (Millimeter).

D in mm ist das geometrische Mittel aus den Grenzwerten D1 und D2 des jeweiligen Nennmaßbereiches:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D = \sqrt[2]{(D_1 \cdot D_2)}}

Die Formel ist empirisch ermittelt, es wurde berücksichtigt, dass unter gleichen Herstellbedingungen die Beziehung zwischen Herstellfehler und Nennmaß in etwa einem parabolischen Verlauf folgt.

Das Glied 0,001 x D berücksichtigt die mit wachsendem Nennmaß linear zunehmende Unsicherheit beim Messen. Die Faktoren 0,45 und 0,001 sind somit Erfahrungswerte.

Passungssysteme

Man unterscheidet zwei grundsätzliche Passungssysteme, nämlich das System Einheitsbohrung und das System Einheitswelle. Weitere Informationen siehe Artikel Passungssystem.

System Einheitsbohrung

Beim System Einheitsbohrung werden alle Bohrungen nach DIN 7154 in der gleichen Toleranz (z. B. H7) ausgeführt. Die gewünschte Passung wird durch Auswahl einer Welle mit entsprechender Toleranz erreicht.

System Einheitswelle

Beim System Einheitswelle werden alle Wellen nach DIN 7155 in der gleichen Toleranz (z. B. h6) ausgeführt. Die gewünschte Passung wird durch Auswahl einer Bohrung entsprechender Toleranz erreicht.

Praxis

Die Herstellung von Wellen mit genauem Durchmesser ist auf einer Drehmaschine mit relativ geringem Aufwand möglich. Die Herstellung von Bohrungen mit genauem Durchmesser erfolgt, besonders bei kleinen Bohrungen, oft durch Reiben und ist aufwendiger, da für jeden Durchmesser und jede Toleranz ein spezielles Werkzeug notwendig ist. Es ist daher zweckmäßig, die Bohrung als Einheitsbohrung auszuführen, pro Nenndurchmesser nur eine Reibahle zu verwenden und die Welle entsprechend anzupassen.

Maximale Kosteneffizienz wird erreicht, wenn die IT der Toleranzfeldbreite von Welle und Bohrung entweder gleich sind oder aus den o. g. Gründen der Herstellbarkeit, die Welle ggf. mit einer i. d. R. nächstkleineren IT ausgelegt wurde, bspw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d^{\text{H7}}_{\text{d8}} } .

Qualität einer Passung (Ist- und Sollwerte)

Die Istwerte einer Passung werden als Messgröße herangezogen und mit den vordefinierten Sollwerten für das entsprechende Passungssystem verglichen. Das Ergebnis dieses Vergleichs wird zur Beurteilung der Qualität einer Passung herangezogen. Als Istwerte einer Passung bezeichnet man die messtechnisch ermittelten Werte einer realen Passung, also die gemessenen Istmaße am entsprechenden Bauteil. Die Istmaße der Passung müssen innerhalb der durch die Abmaße tolerierten Grenzen liegen, andernfalls ist die Passung und damit u. U. das gesamte Bauteil Ausschuss.

Das Thema Ausschuss bei Passungen wird im Abschnitt Wurfpassung näher behandelt.

Arten von Passungen

Grundsätzlich werden drei Arten von Passungen unterschieden. Theoretisch können Bohrungen und Wellen beliebig miteinander kombiniert werden. Durch die Wahl der Toleranzklassen ergibt sich beim Zusammenbau entweder Spiel oder Übermaß zwischen den zu verbindenden Teilen.

Je nach Auswahl entsteht somit eine Spiel-, Übergangs- oder Übermaßpassung. Eine komplette Passungsauswahl für das System Einheitsbohrung wird in DIN 7157 definiert. Für das System Einheitswelle definiert dieselbe Norm ausschließlich Spielpassungen.

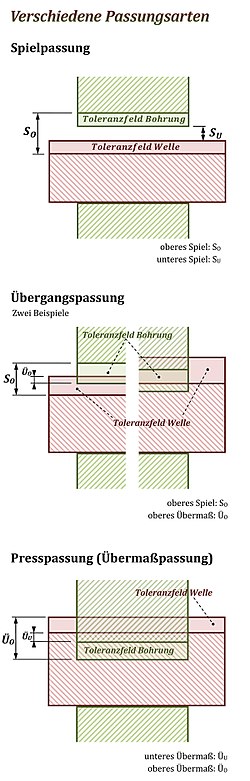
Spielpassung

Das Kleinstmaß der Bohrung ist immer größer als, im Grenzfall auch gleich groß wie, das Größtmaß der Welle.

  • Kombination Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varnothing 30^{\text{H7}}_{\text{f7}}}
Abmaße der Bohrung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varnothing 30^{\text{H7}} = \varnothing 30^{+21}_{ 0} } , der ausgeführte Bohrungsdurchmesser darf zwischen 30,000 und 30,021 mm betragen.
Toleranzbereich: (21 − 0) µm = 21 µm
Abmaße der Welle: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varnothing 30_{\text{f7}} = \varnothing 30^{-20}_{-41} } , der ausgeführte Wellendurchmesser darf zwischen 29,959 und 29,980 mm betragen.
Toleranzbereich: (41 − 20) µm = 21 µm.
Da die Abmaße der korrekt gefertigten H7-Bohrung immer größergleich 0 sind und die Abmaße der f7-Welle immer kleiner als mindestens −20 µm ist, besteht ein minimales Spiel von
(0 µm der Bohrung + 20 µm der Welle) = 20 µm
und ein Größtspiel von
(21 µm der Bohrung + 41 µm der Welle) = 62 µm

Ausgewählte Spielpassungen

Ausgewählte Spielpassungen nach Passungssystem „Einheitsbohrung“

  • Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d^{\text{H7}}_{\text{d9}} } : Teile mit sehr reichlichem Spiel: Transmissionsteile, Lager für Baumaschinen
  • Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d^{\text{H8}}_{\text{e8}} } : Teile mit reichlich Spiel: Hauptlager für Kurbelwellen, Kolben in Zylinder
  • Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d^{\text{H8}}_{\text{f7}} } : Teile mit merklichem Spiel beweglich: Mehrfach gelagerte Welle, Kolben in Zylinder
  • Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d^{\text{H8}}_{\text{h9}} } : Teile haben kaum Spiel und können mit Handkraft verschoben werden: Verschiebbare Zahnräder und Kupplungen
  • Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d^{\text{H7}}_{\text{g6}} } : Teile ohne merkliches Spiel beweglich: Zahnräder und Kupplungen
  • Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d^{\text{H7}}_{\text{h6}} } : Teile von Hand gerade noch verschiebbar: Führungen an Werkzeugmaschinen, Stellringe

Übergangspassung

Bei einer Übergangspassung entsteht je nach Istmaßen von Bohrung und Welle beim Fügen entweder ein Spiel oder ein Übermaß. Das Größtmaß der Bohrung ist größer, im Grenzfall auch gleich groß wie das Kleinstmaß der Welle.

  • Kombination Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varnothing 6^{H7}_{m6} } :
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varnothing 6^{H7} = \varnothing 6^{+12}_{ 0} }
Toleranzbereich: (12 − 0) µm = 12 µm.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varnothing 6_{m6} = \varnothing 6^{+12}_{+4} }
Toleranzbereich: (12 − 4) µm = 8 µm.
Hier findet eine teilweise Überschneidung der Abmaße einer korrekt gefertigten H7-Bohrung und der m6-Welle statt. Je nach Ausführung entsteht ein maximales Spiel von
(+12 µm der Bohrung) − (+ 4 µm der Welle) = 8 µm
oder ein Übermaß von
(0 µm der Bohrung + 12 µm der Welle) = 12 µm

Ausgewählte Übergangspassungen

Ausgewählte Übergangspassungen nach Passungssystem „Einheitsbohrung“

  • Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d^{H7}_{j6} } : Die Teile lassen sich mit leichten Schlägen oder von Hand verschieben.
  • Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d^{H7}_{m6} } : Teile mit geringem Druck fügbar: Spurkränze auf Radkörper
  • Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d^{H7}_{n6} } : Teile mit dem Schlosserhammer fügbar: Zahnräder und Kupplungen auf Zapfen, außerdem gängige Passung für Zylinderstifte zum präzisen Fügen von Bauteilen

Übermaßpassung (Presspassung)

Das Größtmaß der Bohrung ist in jedem Fall kleiner als das Kleinstmaß der Welle.

  • Kombination Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle \varnothing 3_{h6}^{X7}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varnothing 3^{X7} = \varnothing 3^{-20}_{ -30} }
Toleranzbereich: (30 − 20) µm = 10 µm.
Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle \varnothing 3_{h6}=\varnothing 3_{-6}}
Toleranzbereich: (0 − 6) µm = 6 µm.
Hier findet immer eine Überschneidung der Abmaße einer korrekt gefertigten X7-Bohrung und der h6-Welle statt.
Je nach Ausführung entsteht ein unteres (minimales) Übermaß von
(20 µm der Bohrung − 6 µm der Welle) = 14 µm
oder ein oberes (maximales) Übermaß von
(30 µm der Bohrung − 0 µm der Welle) = 30 µm

Ausgewählte Übermaßpassungen

Ausgewählte Übermaßpassungen nach Passungssystem „Einheitsbohrung“

  • Presspassungen
    • Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d^{H7}_{p6} } : Teile mit Druck fügbar: Passfederverbindungen
    • Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d^{H7}_{r6} } : Teile mit größerem Druck fügbar: Welle-Nabe-Verbindungen, Hebelverbindungen
    • Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d^{H7}_{s6} } : Teile mit größerem Druck und zusätzlicher Erwärmung fügbar: Welle-Nabe-Verbindungen

Prüfen von Passungen

Um Passtoleranzen nach der Fertigung zu prüfen, verwendet man in der Mess- und Prüftechnik sogenannte Lehren. Lehren für Passungen heißen Grenzlehren, da man mit deren Hilfe die Maßgrenzen der Passung überprüft. (siehe dazu: Kategorie:Lehre (Technik))

Eine Lehre für Bohrungen ist z. B. der Grenzlehrdorn, ein zylindrischer Stift mit zwei sehr genau gefertigten Prüfzylindern an den Seiten. Nur wenn die „Gutseite“ davon in die Passbohrung passt und die „Ausschussseite“(markiert durch roten Ring) nicht, ist die Passung in Ordnung.

Zur Überprüfung von Wellen kann z. B. eine Grenzrachenlehre verwendet werden. Diese Lehre enthält an beiden Seiten einen länglichen Spalt, der durch zwei ebene, parallele Flächen begrenzt ist. Auch hier darf und muss die Welle nur in genau einen der beiden Spalte passen.

Zu beachten ist jedoch, dass für jede einzelne Passung ein eigener Lehrdorn bzw. eine eigene Rachenlehre benötigt wird. Lehren liefern keinen Messwert, deshalb verwendet man in der Serienfertigung häufig induktive Messtaster oder pneumatische Messgeräte, deren Ergebnisse werden dann in der Statistischen Prozesskontrolle weiterverarbeitet.

Wurfpassung (Ausschuss)

Der Begriff Wurfpassung ist eine pseudofachliche Umschreibung für eine nicht bemerkte, besonders misslungene Passung mit unerwünscht viel Spiel. Der Begriff rührt daher, dass man sich zutrauen würde, die Welle auch durch Werfen aus der Entfernung in die Bohrung zu bekommen.

Ein oder beide Passungsteile sind außerhalb der Toleranz gefertigt. Üblicherweise werden in der Produktion Stichproben entnommen und nicht konforme Teile gelten als Fehlproduktion, auch Ausschuss genannt, der nicht oder nur mit erheblichem Aufwand auf das korrekte Maß gebracht werden kann. Üblicherweise ist ein solches Teil unbrauchbar und wird der Verwertung, beispielsweise dem Schrott, zugeführt. Zudem muss ein fehlerhaftes Werkstück mit zum Teil hohem Aufwand neu hergestellt werden, insbesondere wenn der Fehler gegen Ende der Produktion auftritt und dem Werkstück eine hohe Fertigungstiefe anhaftet.

Siehe auch

Literatur

  • Eberhard Felber, Klaus Felber: Toleranzen und Passungen. 14. Auflage. Fachbuchverlag, Leipzig 1989, ISBN 3-343-00021-3.
  • Ulrich Fischer, Max Heinzler, u. a.: Tabellenbuch Metall. Verlag Europa-Lehrmittel, 43. Auflage, 2005, ISBN 3-8085-1723-9.

Weblinks

Commons: Passungen – Sammlung von Bildern, Videos und Audiodateien
Wiktionary: Passung – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen
Abgerufen von „https://de.wikiup.org/index.php?title=Passung&oldid=220059062“