Picard-Iteration

Als Picard-Iteration bezeichnet man in der Mathematik die von Charles Émile Picard entdeckte Fixpunktiteration zur approximativen Lösung von gewöhnlichen Differentialgleichungen, die auch in dem Beweis der lokalen Version des Satzes von Picard-Lindelöf verwendet wird.

Definition

Betrachte das durch

$x'(t)=f(t,x(t)),\quad x(t_{0})=x_{0}$

gegebene Anfangswertproblem, wobei $f(t,x)$ eine stetige und im zweiten Argument lipschitzstetige Abbildung und $t$ aus einem reellen Zeitintervall ist.

Die Picard-Iteration ist dann gegeben durch

$x^{[0]}(t)=x_{0}$

Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle x^{[\ell +1]}(t)=x_{0}+\int _{t_{0}}^{t}f(s,x^{[\ell ]}(s))\,ds,\quad t\in [t_{0},t_{0}+\varepsilon ].}

Die dadurch erzeugte Funktionenfolge konvergiert für hinreichend kleine Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon > 0} gleichmäßig gegen die Lösung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x(t)} .

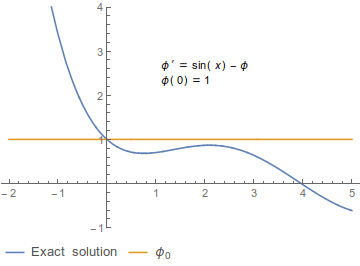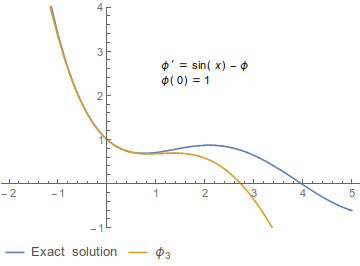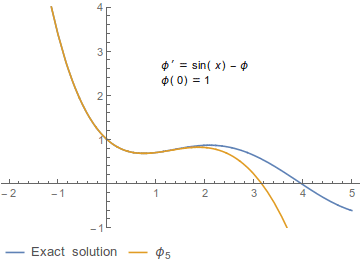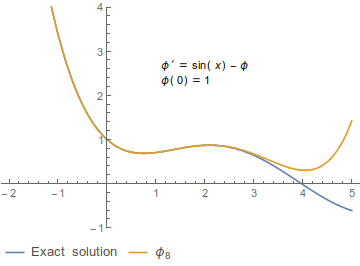
Beispiel

Animation zur Entwicklung der durch Picard-Iteration erzeugten Funktionenfolge.

Eine gewöhnliche Differentialgleichung sei gegeben durch

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x' = \sin(t) - x}

mit dem Startwert:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x(0) = 1}

Zwei Schritte der Picard-Iteration lauten:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^{[0]}(t) = 1}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^{[1]}(t) = 1 + \int_0^t (\sin(s) - 1)\, ds = 2 - \cos(t) - t}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^{[2]}(t) = 1 + \int_0^t (\sin(s) - (2 - \cos(s) - s))\, ds = 2 - \cos(t) - 2t + \sin(t) + \frac{t^2}{2}}

Weblinks

Wikibooks

Wikibooks: Beweisarchiv - Beweis der Behauptung – Lern- und Lehrmaterialien