Spannungsquelle

Als Spannungsquelle wird in der Schaltungstheorie der Elektrotechnik ein aktiver Zweipol bezeichnet, der zwischen seinen Anschlusspunkten eine elektrische Spannung liefert. Als wesentliche Eigenschaft hängt diese Spannung nur gering oder – beim Modell der idealen Spannungsquelle im Rahmen der Netzwerkanalyse – gar nicht von der elektrischen Stromstärke ab, welcher der Quelle entnommen wird.^[1]^[2] Die gelieferte elektrische Spannung ist im Idealfall somit unabhängig vom jeweilig angeschlossenen Verbraucher. Realisiert die Spannungsquelle das Modellverhalten innerhalb nur kleiner Abweichungen, so wird sie auch als Konstantspannungsquelle bezeichnet oder, wenn sie besonders präzise ist, als Referenzspannungsquelle.

Eine Spannungsquelle dient vorzugsweise als elektrische Energiequelle, die abhängig vom angeschlossenen Verbraucher elektrischen Strom liefert, dabei aber nicht mit einer Stromquelle (siehe unten) verwechselt werden darf. Ferner kommt sie als Lieferant von elektrischen Signalen vor.

Eine Spannungsquelle kann auch ein Gegenstand sein, der lediglich ein elektrisches Feld erzeugen kann, dabei aber nur kurzzeitig oder in nicht verwertbarem Umfang zur Stromabgabe fähig ist.

Schaltzeichen gemäß DIN EN 60617-2 für eine ideale Gleichspannungsquelle mit der elektrischen Spannung

U

Zusammenhang

Das Gegenstück zur Spannungsquelle im Rahmen der elektrischen Netzwerkanalyse ist der Zweipol einer Stromquelle, welcher einen bestimmten elektrischen Strom liefert – unabhängig von der an ihren Klemmen anliegenden Spannung. Eine beliebige Anordnung von linearen Spannungs- und Stromquellen und Widerständen in Form einer elektrischen Schaltung lässt sich nach außen immer als Zweipol durch nur eine Spannungsquelle mit einem Innenwiderstand vollständig beschreiben. Dieser Zusammenhang wird auch als das Thévenin-Theorem bezeichnet und spielt in der elektrischen Schaltungsanalyse eine Rolle, da sich damit komplizierte Schaltungen auf vereinfachte Ersatzschaltungen reduzieren lassen, die dann der Analyse leichter zugänglich sind.

In den Ersatzschaltungen wird die Spannungsquelle immer als von der Stromstärke unabhängig angesehen. Dieses Verhalten ist in Realität nur näherungsweise zu erreichen; dann sind im Ersatzschaltbild zur besseren Beschreibung der Realität weitere Bauelemente einzufügen. Im einfachsten Fall dient dazu ein mit der Spannungsquelle in Reihe liegender ohmscher Innenwiderstand.^[3]^[4]^[5]^[6]^[7] Bei technisch genutzten Spannungsquellen wird im Regelfall versucht, den Innenwiderstand möglichst klein zu halten.

Arten von Spannungsquellen

Gleich- und Wechselspannungsquellen

Gleichspannungsquellen halten ihren Spannungswert zeitlich konstant. Solche Quellen, die als Energiequellen arbeiten, sind z. B. Batterien, Akkumulatoren und Netzgeräte. Ferner gibt es Spannungsquellen, die zwar wenig belastbar sind, aber als Signalquellen oder Messfühler bedeutsam sind, z. B. Thermoelemente.

Entsprechend erzeugt eine Wechselspannungsquelle eine sich zeitlich periodisch verändernde Spannung. Zu diesen Quellen gehören z. B. Generatoren, Transformatoren, Signalgeneratoren und ebenfalls Netzgeräte. Auch das elektrische Energieversorgungsnetz stellt eine Wechselspannungsquelle dar. Ferner gibt es auch hier wenig belastbare Quellen, etwa zur Übermittlung von Nachrichten oder zur Weitergabe von Mess- und Tonsignalen, z. B. Mikrofone.

Asymmetrische, bipolare und symmetrische Spannungsversorgungen

Schaltbild für symmetrische Spannungsquelle

Hat eine Gleichspannungsquelle zwei Anschlüsse, von denen einer zum allgemeinen Bezugs- oder Massepotential erklärt wird, so spricht man von einer asymmetrischen Spannungsquelle.

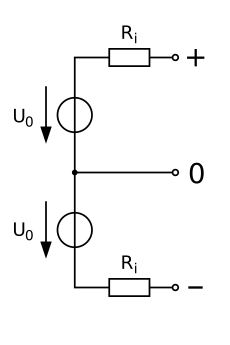
Bei einer bipolaren Gleichspannungsversorgung werden gleichzeitig eine positive und negative Spannung, bezogen auf ein gemeinsames Massepotential, z. B. +15 V und −10 V, bereitgestellt. Sind die positive und negative Spannung zudem in ihren Beträgen gleich groß, so handelt es sich um eine symmetrische Gleichspannungsversorgung. Eine derartige Spannungsversorgung wird häufig für Baugruppen benötigt, die Wechselspannungen verarbeiten, beispielsweise Audioverstärker.

Gesteuerte und geregelte Spannungsquellen

Neben der unabhängigen Spannungsquelle mit einer festen Quellenspannung gibt es die gesteuerte Spannungsquelle, deren Quellenspannung eine Funktion einer äußeren Spannung oder Stromstärke ist, die dazu an getrennten Anschlusspunkten angeschlossenen wird.

Statt über eine solche äußere Stellgröße wird die geregelte Spannungsquelle über einen Regelkreis so geführt, dass sich die Ausgangsspannung auf einen vorgegebenen Sollwert einstellt. Dadurch werden Störeinflüsse durch Veränderung der Strombelastung, Schwankungen der Netzspannung oder Temperaturdrift kompensiert. Mit manchen Labornetzteilen kann auch die Spannung am Verbraucher-Eingang (statt Quellen-Ausgang) geregelt werden, wodurch auch Einflüsse der Leitungen und Kontakte ausgeregelt werden. Dabei ist unerheblich, ob es sich bei der geregelten Spannungsquelle um eine Gleich- oder Wechselspannungsquelle handelt.

Technische Beschreibungen

Grundlagen

In diesem Artikel werden folgende Bezeichnungen verwendet:

Ausgangs- oder Klemmenspannung $U_{\mathrm {kl} }$
Quellenspannung $U_{0}$ , früher auch als Urspannung oder Elektromotorische Kraft (EMK) bezeichnet

Dabei ist

U_{0}

die maximale Spannung, die die Quelle liefern kann. Sie entsteht, wenn die Klemmen offen sind (Leerlauf).

Kurzschlussstromstärke $I_{\mathrm {K} }$

Dabei ist

I_{\mathrm {K} }

die maximale Stromstärke, die die Quelle liefern kann. Sie entsteht, wenn die Klemmen widerstandslos miteinander verbunden sind (Kurzschluss).

Innenwiderstand $R_{\mathrm {i} }$ , auch als Quellwiderstand $R_{\mathrm {Q} }$ bezeichnet
Verbraucherwiderstand $R_{\mathrm {V} }$ , auch als Lastwiderstand $R_{\mathrm {L} }$ oder Eingangswiderstand $R_{\mathrm {e} }$ einer Folgeschaltung bezeichnet

Ferner wird folgende Zählrichtung verwendet:

Bei einem passiven Bauteil oder Verbraucher soll sich die Bezugsrichtung der Stromstärke auf die Polarität der Spannung beziehen.^[8] Durch ein Verbraucherzählpfeilsystem wie im nachfolgenden Ersatzschaltbild wird erreicht, dass Spannung und Stromstärke dasselbe Vorzeichen haben. Eine positive Spannung $U_{\mathrm {kl} }$ von a nach b erzeugt im Verbraucher eine positive Stromstärke $I$ von a nach b. (Bei Umkehr eines der beiden Pfeile müsste in das ohmsche Gesetz ein Minuszeichen eingefügt werden.) Durch die konsequente Verwendung der Vorzeichen in der gesamten Schaltung fließt im Inneren der Spannungsquelle der Strom der Spannung entgegen.

Ideale und reale Spannungsquellen

Ersatzschaltbild einer realen linearen Spannungsquelle (mit Verbraucher)

Als ideale Spannungsquelle wird eine Quelle bezeichnet, die unabhängig vom nachgeschalteten Verbraucher stets dieselbe Spannung abgibt. Klemmen- und Quellenspannung sind somit identisch; der Energievorrat der Quelle wird als unendlich angenommen. Da dies in der Praxis in Strenge unmöglich zu erreichen ist, werden in technischen Berechnungen zumeist Ersatzschaltungen für reale Spannungsquellen eingesetzt. So hat sich die lineare Spannungsquelle aus einer Reihenschaltung einer idealen Spannungsquelle und einem ohmschen Innenwiderstand bewährt, weil sie viele Erscheinungen mit zufriedenstellender Genauigkeit beschreibt. Mit diesem erweiterten Modell kann bei Berechnungen der Einfluss von nachgeschalteten Lasten auf die tatsächlich anliegende Klemmenspannung der Quelle nachvollzogen werden. Je stärker die Quelle vom Verbraucher belastet wird, desto tiefer sinkt die an den Klemmen anliegende Spannung. Der Innenwiderstand begrenzt die maximale Stromstärke, die im Kurzschlussfall ( $R_{\mathrm {V} }=0$ ) möglich ist. Die Kurzschlussstromstärke berechnet sich dann zu

I_{\mathrm {K} }={\frac {U_{0}}{R_{\mathrm {i} }}}

Die maximale Stromstärke ist also umso größer, je kleiner der Innenwiderstand der Quelle ist. In der Praxis kann sich der Innenwiderstand einer Spannungsquelle mit der Belastung und mit der Zeit verändern; beispielsweise ist der Innenwiderstand einer neuen Batterie viel geringer als derjenige einer verbrauchten.

Bei Spannungsquellen in der Funktion als Energiequelle ist anzustreben, dass ihr Innenwiderstand so klein wie möglich bleibt, jedenfalls viel kleiner als der des Verbrauchers. Damit besteht andererseits die Gefahr eines zerstörerischen Überstroms bei Kurzschlüssen, weshalb der Überstrom schnell durch Sicherungen abgeschaltet werden muss. Bei elektronischen Spannungsquellen ist im Gegensatz zum Modell der idealen Spannungsquelle der abgebbare Strom begrenzt. Überschreitet der Strom eine bestimmte Grenze, kann die Spannung einbrechen.

Bei Spannungsquellen in der Funktion als Signalquelle, die nur begrenzt Leistung erzeugen können, gelten andere Gesichtspunkte, siehe weiter unten im Abschnitt Leistung.

Kennlinien

Kennlinien idealer (rot), linearer (türkis) und nichtlinearer (grün) Spannungsquellen

Die Klemmenspannung $U_{\mathrm {kl} }$ einer Spannungsquelle mit der Quellenspannung $U_{0}$ als Funktion der entnommenen Stromstärke $I$ kann grafisch als Kennlinie dargestellt werden.

Bei einer idealen Spannungsquelle ist diese gemäß der Definition eine waagerechte Gerade. Sie ist nebenstehend als rote Linie dargestellt.
Eine reale Spannungsquelle mit einem Innenwiderstand $R_{\text{i}}>0$ liefert eine fallende Kennlinie, bei der die Spannung mit steigender Stromstärke abnimmt. Für das oben gezeigte Ersatzschaltbild gilt:

U_{\text{kl}}=U_{0}-I\,R_{\text{i}}

.

Bei einer linearen Quelle mit einem ohmschen Innenwiderstand ergibt das eine geneigte Gerade. Dazu sind zwei Kennlinien mit unterschiedlichem Innenwiderstand in der Farbe Türkis dargestellt. Sie erreichen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_\mathrm{kl}=0} bei der jeweils zutreffenden Kurzschlussstromstärke Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_\mathrm K} .
Eine nichtlineare Quelle weist eine gekrümmte Kennlinie auf. Ein Beispiel einer solchen Quelle ist die Solarzelle. Deren Verhalten ist in Grün dargestellt. Nur im flachen Bereich ihrer Kennlinie kann diese Quelle als Spannungsquelle angesehen werden, im steilen Bereich bei Annäherung an den Kurzschluss wird ihr Verhalten durch eine Stromquelle angemessener beschrieben. Jeder Einzelfall von Nichtlinearität erfordert eine spezielle Ersatzschaltung, so dass hier keine Einzelheiten behandelt werden können.

Parallel- und Reihenschaltung von Spannungsquellen

Reihenschaltung

Wird mehr Spannung vom Verbraucher benötigt, als eine einzelne Quelle liefern kann, so ergibt die Reihenschaltung mehrerer potentialfreier Spannungsquellen eine Gesamtspannung aus der Summe der Spannungen der einzelnen Spannungsquellen. Ebenso ist der Gesamtquellwiderstand gleich der Summe der einzelnen Innenwiderstände. Der Strom ist für alle Quellen in Betrag und Vorzeichen oder in Frequenz, Phasenwinkel und Scheitelwert identisch.

Parallelschaltung

Wird mehr Strom vom Verbraucher benötigt, als eine einzelne Quelle liefern kann, so dass eine Parallelschaltung von Spannungsquellen erforderlich wird, so ist dies nur bedingt und nur mit realen Quellen möglich. Dazu müssen bei Bedarf Quellenwiderstände durch externe in die Leitungen geschaltete Widerstände nachgebildet werden. Diese müssen so groß sein, dass durch ihre Spannungsverluste die Spannung am Verbraucher kleiner wird als die kleinste der Leerlaufspannungen. Stets ist darauf zu achten, dass alle parallelgeschalteten Spannungsquellen

bezüglich der Klemmenspannung denselben Betrag annehmen können,
bei Gleichspannung dasselbe Vorzeichen (Polung) oder bei Wechselspannung denselben Phasenwinkel aufweisen,
potentialfrei sind oder an demselben Pol geerdet sind; bei mehr als einem Erdpunkt können Ausgleichsströme fließen (siehe Brummschleife).

Werden diese Punkte nicht beachtet, führt dies zu einem meist unerwünschten Strom zwischen den Quellen. Je nach Stromhöhe oder Ausführung der Spannungsquellen kann dies zur Zerstörung einzelner Teilquellen führen. Diese Kriterien können auch mit entsprechenden elektronischen Schutzschaltungen, die die Spannungen der einzelnen Spannungsquellen überwachen und regeln, erfüllt werden.

Die Gesamtspannung von mehreren parallelgeschalteten Spannungsquellen ist abhängig von den Quellenspannungen und den Innenwiderständen der einzelnen Spannungsquellen, wie oben beschrieben. Der Gesamtstrom ergibt sich aus der Summe der Ströme der einzelnen Quellen. Um den Innenwiderstand zu berechnen, sind die einzelnen Spannungsquellen zu Stromquellen zu transformieren (siehe weiter unten), der Widerstand kann dann aus der Parallelschaltung der einzelnen Innenwiderstände berechnet werden.

Leistung

In Blick auf die elektrische Leistung sind bei einer Spannungsquelle zu unterscheiden

die von der Quelle erzeugbare Leistung,
die im Zusammenhang mit einem Verbraucher erzeugte Leistung,
die einem Verbraucher zugeführte Leistung.

Die meisten in der Praxis vorkommenden Spannungsquellen verhalten sich bei bestimmungsgemäßem Einsatz wie das Modell der linearen Quelle mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_\mathrm i\ll R_\mathrm V} ; dann gilt Spannungsanpassung unabhängig von der Stromstärke oder Belastung. Dazu muss die von der Quelle erzeugbare Leistung deutliche Reserven haben gegenüber der tatsächlich erzeugten.

Gemäß Ersatzschaltbild gilt bei einer realen Spannungsquelle mit dem Innenwiderstand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_\mathrm i} zusammen mit einem Verbraucherwiderstand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_\mathrm V}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_\text{kl}=U_0 -I\,R_\text{i} =I\,R_\text{V}} .

Bei den beiden Grenzfällen des Verbraucherwiderstandes, bei Kurzschluss Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (U_\text{kl}=0)} und Unterbrechung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (I=0)} , wird dem Verbraucher keine Leistung zugeführt. Dazwischen ist diese Leistung größer als null; somit erhält der Verbraucher bei einem bestimmten Widerstandswert zwischen den Grenzfällen ein Maximum an Leistung. Dieser Fall heißt Leistungsanpassung. Er tritt auf, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_\mathrm V =R_\mathrm i} ist. Die maximal zugeführte Leistung ergibt sich zu

Normierte Ausgangsleistung und Wirkungsgrad einer realen Spannungsquelle in Abhängigkeit vom Widerstandsverhältnis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_\mathrm a /R_\mathrm i} aus Verbraucherwiderstand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_\mathrm a} (im Text Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_\mathrm V} ) zu Innenwiderstand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_\mathrm i}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P_\text{zu max} = \frac{{U_0}^2}{4\, R_\mathrm i}} .

Bei Spannungsquellen für die Energielieferung wird diese niemals abgerufen, sondern nur bei leistungsschwachen Quellen wie z. B. Antennen. Bei in Leistungsanpassung betriebenen Quellen erhält von der erzeugten Leistung der Verbraucher die Hälfte.

Die Verlustleistung des Innenwiderstandes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_\mathrm i}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P_\mathrm i = I^2\, R_\mathrm i}

wird nahezu vollständig in thermische Leistung umgewandelt. Sie ist dafür mitverantwortlich, dass sich z. B. Batterien beim Entladen sowie Akkumulatoren auch beim Laden erwärmen. Bei einem Kurzschluss kann die am Innenwiderstand umgewandelte Wärmeenergie die Spannungsquelle und in deren Nähe befindliche Gegenstände durch Hitze beschädigen, zerstören oder in Brand versetzen.

Der Wirkungsgrad Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \eta} einer Spannungsquelle ergibt sich aus dem Verhältnis der dem Verbraucher zugeführten Leistung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P_\text{zu}= I\,U_\text{kl}} zur von der Spannungsquelle erzeugten Leistung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P_\text{erz} =I\,U_0} . Bei der realen Spannungsquelle geht ein Teil der erzeugten Spannung an Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_\text{i}} verloren. Bei gleicher Stromstärke im gesamten Strompfad geht entsprechend auch ein Teil der Leistung an Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_\text{i}} verloren. Für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0<R_\text{V} <\infty} gilt

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \eta =\frac{I^2R_\text{V}} {I^2R_\text{i}+I^2R_\text{V}} =\frac{R_\text{V}}{R_\text{i}+R_\text{V}}} .

Für einen möglichst hohen Wirkungsgrad soll Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_\mathrm i\ll R_\mathrm V} sein, das ist der Zustand der Spannungsanpassung. Im Grenzfall der idealen Spannungsquelle wird Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \eta =1} .

Transformation Spannungsquelle ↔ Stromquelle

Thévenin-Äquivalent und Norton-Äquivalent

Gemäß den Thévenin- und Norton-Theoremen lässt sich jede lineare Spannungsquelle auch als eine lineare Stromquelle ansehen. Welchen Begriff verwendet wird, hängt davon ab, zu welcher Idealform das Verhalten der Quelle näher gesehen wird. Die nachfolgenden Gleichungen lassen sich ineinander umrechnen, die linken beschreiben die Spannungsquelle, die rechten die Stromquelle.

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_\mathrm{kl} = U_0 -I \cdot R_\mathrm i \quad \Leftrightarrow \quad I = I_\mathrm K - U_\mathrm{kl} \cdot \frac 1{R_\mathrm i} }

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_\mathrm{kl} = U_0 -I\frac{U_0}{I_\mathrm K} \quad \Leftrightarrow \quad I = I_\mathrm K -U_\mathrm{kl}\;\;\frac{I_\mathrm K}{U_0}}

Literatur

Karl Küpfmüller, Wolfgang Mathis, Albrecht Reibiger: Theoretische Elektrotechnik. 18. Auflage. Springer, 2008, ISBN 978-3-540-78589-7.
sowie die in den Einzelnachweisen aufgeführten Fachbücher

Einzelnachweise

↑ IEC 60050, siehe DKE Deutsche Kommission Elektrotechnik Elektronik Informationstechnik in DIN und VDE: Internationales Elektrotechnisches Wörterbuch IEV Eintrag 131-12-21.
↑ DIN EN 60375:2004-04, Nr. 8.1.1
↑ Wilfried Weißgerber: Elektrotechnik für Ingenieure, Band 1.
↑ Heinrich Frohne, Karl-Heinz Löcherer, Hans Müller: Moeller Grundlagen der Elektrotechnik.
↑ Ulrich Tietze und Christoph Schenk: Halbleiterschaltungstechnik.
↑ Ralf Kories und Heinz Schmidt-Walter: Taschenbuch der Elektrotechnik.
↑ Rainer Ose: Elektrotechnik für Ingenieure, Band 1.
↑ DIN EN 60375, Nr. 6.1

[IEV-1] IEC 60050, siehe DKE Deutsche Kommission Elektrotechnik Elektronik Informationstechnik in DIN und VDE: Internationales Elektrotechnisches Wörterbuch IEV Eintrag 131-12-21.

[2] DIN EN 60375:2004-04, Nr. 8.1.1

[3] Wilfried Weißgerber: Elektrotechnik für Ingenieure, Band 1.

[4] Heinrich Frohne, Karl-Heinz Löcherer, Hans Müller: Moeller Grundlagen der Elektrotechnik.

[5] Ulrich Tietze und Christoph Schenk: Halbleiterschaltungstechnik.

[6] Ralf Kories und Heinz Schmidt-Walter: Taschenbuch der Elektrotechnik.

[7] Rainer Ose: Elektrotechnik für Ingenieure, Band 1.

[8] DIN EN 60375, Nr. 6.1

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

Anonym

Suche

Spannungsquelle

Namensräume

Mehr

Seitenaktionen

Inhaltsverzeichnis

Zusammenhang