Transinformation

Transinformation oder gegenseitige Information (engl. mutual information) ist eine Größe aus der Informationstheorie, die die Stärke des statistischen Zusammenhangs zweier Zufallsgrößen angibt. Die Transinformation wird auch als Synentropie bezeichnet. Im Gegensatz zur Synentropie einer Markov-Quelle erster Ordnung, welche die Redundanz einer Quelle zum Ausdruck bringt und somit minimal sein soll, stellt die Synentropie eines Kanals den mittleren Informationsgehalt dar, der vom Sender zum Empfänger gelangt und somit maximal sein soll.

Ein gedächtnisloser Kanal verbindet die zwei Quellen X und Y. Von X nach Y fließt Transinformation. Die Empfänger-Quelle Y der Entsende-Quelle X verhält sich wie eine Quelle. Es wird nicht zwischen Empfänger und Entsender unterschieden. Je mehr die Quellen voneinander abhängen, desto mehr Transinformation ist vorhanden.

Gelegentlich wird auch die Bezeichnung relative Entropie verwendet, diese entspricht jedoch der Kullback-Leibler-Divergenz.

Die Transinformation steht in einem engen Zusammenhang zur Entropie und zur bedingten Entropie. So berechnet sich die Transinformation $I(X;Y)$ folgendermaßen:

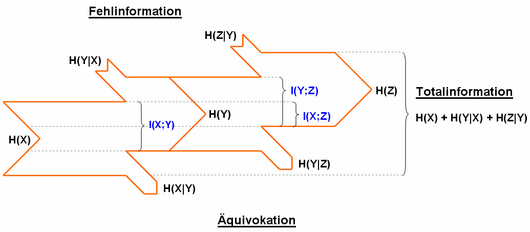
Definition über die Differenz von Quell-Entropie und Äquivokation bzw. Empfangs-Entropie und Fehlinformation:

$I(X;Y)=H(X)-H(X\vert Y)=H(Y)-H(Y\vert X).$

Definition über Wahrscheinlichkeiten:

$I(X;Y)=\sum _{x}{}\sum _{y}{}p(x,y)\cdot \log _{2}\left({\frac {p(x,y)}{p(x)p(y)}}\right).$

Definition über die Kullback-Leibler-Divergenz:

$I(X;Y)=D(p(x,y)\|p(x)p(y)).$

Definition über den Erwartungswert:

$I(X;Y)=E\left\{\log _{2}\left({\frac {p(x,y)}{p(x)p(y)}}\right)\right\}.$

Verschwindet die Transinformation, so spricht man von statistischer Unabhängigkeit der beiden Zufallsgrößen. Die Transinformation wird maximal, wenn sich eine Zufallsgröße vollkommen aus der anderen berechnen lässt.

Zwei gedächtnislose Kanäle verbinden drei Quellen. Von der Senderquelle X kann der Empfängerquelle Y eine Transinformation von I(x;y) übermittelt werden. Wird diese Transinformation weiter geleitet so empfängt die Empfängerquelle Z eine Transinformation von I(X;Z). Man kann hier deutlich sehen, dass die Transinformation von der Menge an Äquivokation abhängt.

Die Transinformation beruht auf der von Claude Shannon eingeführten Definition der Information mit Hilfe der Entropie (Unsicherheit, mittlerer Informationsgehalt). Nimmt die Transinformation zu, so verringert sich die Unsicherheit über eine Zufallsgröße unter der Voraussetzung, dass die andere bekannt ist. Ist die Transinformation maximal, verschwindet die Unsicherheit folglich. Wie aus der formalen Definition zu sehen ist, wird die Ungewissheit einer Zufallsvariable durch Kenntnis einer anderen reduziert. Dies drückt sich in der Transinformation aus.

Die Transinformation spielt beispielsweise bei der Datenübertragung eine Rolle. Mit ihr lässt sich die Kanalkapazität eines Kanals bestimmen.

Entsprechend kann auch eine Entropie H(Z) von zwei verschiedenen, wiederum voneinander abhängigen, Entropien abhängen:

In der Fachliteratur werden verschiedene Begriffe verwendet. Die Äquivokation wird auch als „Verlustentropie“ und die Fehlinformation auch als „Irrelevanz“ bezeichnet. Die Transinformation wird auch als „Transmission“ oder „mittlerer Transinformationsgehalt“ bezeichnet.

Literatur

• Martin Werner: Information und Codierung. Grundlagen und Anwendungen, 2. Auflage, Vieweg + Teubner Verlag, Wiesbaden 2008, ISBN 978-3-8348-0232-3.
• Herbert Schneider-Obermann: Basiswissen der Elektro-, Digital- und Informationstechnik. 1. Auflage. Friedrich Vieweg & Sohn Verlag / GWV Fachverlage GmbH, Wiesbaden 2006, ISBN 978-3-528-03979-0.
• D. Krönig, M. Lang (Hrsg.): Physik und Informatik — Informatik und Physik. Springer Verlag, Berlin/Heidelberg 1991, ISBN 978-3-540-55298-7.

Weblinks

• Peter E. Latham, Yasser Roudi: Mutual information. In: Scholarpedia. (englisch, inkl. Literaturangaben)
• Informationskanäle und ihre Kapazität (abgerufen am 26. Februar 2018)
• Entropy, Transinformation and Word Distribution of Information{Carrying Sequences (abgerufen am 26. Februar 2018)
• Informations und Kodierungstheorie (abgerufen am 26. Februar 2018)
• Formeln und Notizen Informationstheorie (abgerufen am 26. Februar 2018)