YCbCr-Farbmodell

CbCr-Fläche des YCbCr-Farbmodells im RGB-Farbraum auf einer Helligkeitsebene von Y = 0,5

Das YCbCr-Farbmodell wurde für das Digitalfernsehen nach der Norm PAL entwickelt, wird heute aber auch beim digitalen NTSC-Fernsehen genutzt. Außerdem wird es beim CCIR-601-Standard für digitale Bild- und Videoaufzeichnung, bei JPEG-Bildern, MPEG-Videos und damit auch bei DVDs, Video-CDs sowie den meisten anderen digitalen Videoformaten verwendet.

Das YCbCr-Modell teilt die Farbinformation in die Grundhelligkeit Y und die zwei Farbkomponenten Cb (

Blue-Yellow Chrominance

) und Cr (

Red-Green Chrominance

) auf. Mit Y wird hier die Helligkeitsachse aus dem CIE-Normvalenzsystem verwendet. Sie entspricht der Hellempfindlichkeit des Auges, die im grünen Spektralbereich am größten ist (V-Lambda-Kurve). Chrominance oder kurz Chroma bedeutet Buntheit im Allgemeinen und Farbigkeit in Bezug auf Helligkeit-Farbigkeits-Modelle.

Originalfarbbild oben und die Aufspaltung dieses Bildes in die Komponenten Y, Cb und Cr. Die Unschärfe in den Farbkomponenten Cb und Cr macht anschaulich, warum die Farbinformation in der Auflösung reduziert werden kann (

downsampling

) ohne den Bildeindruck wesentlich zu verschlechtern. Personen mit einer Rot-Grün-Sehschwäche können eventuell die Cr-Farbkomponente im letzten Teilbild nur eingeschränkt wahrnehmen und sehen nur eine einheitlich graue Fläche.

Allgemeines

Farbmodelle, die einen Farbort nicht wie der RGB-Farbraum durch drei Grundfarben angeben, sondern durch Helligkeit und Farbigkeit, nennt man Helligkeit-Farbigkeit-Modelle. Die Koordinaten sind etwa die Grundhelligkeit (von Schwarz über Grau bis Weiß), der Farbton mit dem größten Anteil sowie die Sättigung der Farbe (von „knallig“ bis blass).

Wie das YUV-Farbmodell für analoges Farbfernsehen, bei dem die Grundhelligkeit dem reinen Schwarzweiß-Bild entspricht, ist das YCbCr-Modell ein reines Helligkeit-Farbigkeits-Modell. Vergleicht man die beiden Separationen des Bildbeispiels in YUV und YCbCr, wird ersichtlich, dass der Helligkeitskanal ein völlig unbuntes Graustufenbild zeigt und, dass lediglich die Chrominanzachsen U und V in der Farbtafel andere Farbtöne durchschneiden als Cb und Cr, wie die jeweilige Farbtafel darüber beweist. Cb ist also ein Maß für die Abweichung der Farbigkeit von Grau in Richtung Blau/Gelb, Cr ist die entsprechende Maßzahl in Richtung Rot/Türkis.

Man beachte, dass ein Farbmodell noch kein Farbraum ist, denn es legt noch nicht fest, welche Farben mit „Rot“, „Grün“ und „Blau“ genau gemeint sind. Für einen Farbraum bedarf es zusätzlich noch des Bezuges auf absolute Farbwerte. Darüber hinaus unterscheiden sich beide Farbmodelle vom ähnlich strukturierten CIELAB-Farbraum dadurch, dass Helligkeit, Chrominanzen und Farbtöne nicht empfindungsgemäß gleichabständig aufgebaut sind.

Analogie zum Sehsinn

Die unterschiedliche Wahrnehmung von Y gegenüber den Cb- und Cr-Kanälen entspricht der Entwicklung der Farb- und Helligkeitsverteilung in der Natur. Viele Informationen sind in der Helligkeit gespeichert, die Farbe variiert kaum.

Im Laufe der Evolution hat sich der menschliche Sehsinn daran angepasst. Das Auge kann geringe Helligkeitsunterschiede besser erkennen als kleine Farbtonunterschiede, und diese wiederum besser als kleine Farbsättigungsunterschiede. So ist ein Text grau auf schwarz geschrieben gut zu lesen, blau auf rot geschrieben bei gleicher Grundhelligkeit jedoch nur sehr schlecht.

Wie in jedem an die menschliche visuelle Wahrnehmung angelehnten Helligkeit-Farbigkeits-System liegen sich auch im YCbCr-Farbraum Farben gegenüber, die sich gegenseitig ausschließen. Das heißt, ein Blau kann nie gelbliche Nuancen (und umgekehrt) und ein Rot nie Grün- oder Türkis-Nuancen (und umgekehrt) aufweisen. Diese Struktur entspricht der Verarbeitung der Farbinformation im Auge und Gehirn (Hering'sche Gegenfarbtheorie).

Farbunterabtastung

Die Analogie zum menschlichen Sehsinn wird für einen großen Vorteil von YCbCr genutzt: die Farbunterabtastung (engl.

chroma subsampling

). Dabei wird die Abtastrate und damit die Datenmenge der Chrominanz-Kanäle Cb und Cr gegenüber der Abtastrate des Luminanz-Kanals Y reduziert, ohne dass es zu einer spürbaren Qualitätsverringerung kommt. So kann man z. B. mit der JPEG-Komprimierung 50 % der Datenmenge einsparen.

Umrechnung zwischen RGB und YCbCr

Vor der Umrechnung müssen die Werte für RGB mit einer Gammakorrektur auf das Intervall [0;1] normiert werden. Das gebildete Farbtripel wird zur Unterscheidung in der Literatur meist mit R′G′B′ bezeichnet. Die YCbCr-Werte sind auf eine bestimmte Auflösung digitalisiert und bei Bedarf mit einem Offset versehen, um negative Werte zu vermeiden. Bevor also die YCbCr-Daten bestimmt werden können, werden aus den R′G′B′-Farbdaten die so genannten YPbPr-Werte berechnet. Diese Werte von YPbPr sind fix auf den Wertebereich [0;1] für Y und [−0,5; +0,5] für die beiden Farbkomponenten PbPr beschränkt und unterliegen keinerlei Beschränkung betreffend der Auflösung, es sind analoge Signale. Durch eine bestimmte Auflösung, beispielsweise 8 Bit pro Wert mit einem Wertebereich von {0, 1, …, 255}, werden aus den Y′PbPr-Werten die Werte Y′CbCr gebildet, jeweils im Wertebereich von {0, 1, …, 255}. Es kann aber auch bei Y′CbCr eine Abbildung auf 10 Bit mit einem Wertebereich von {0, 1, …, 1023} erfolgen. Diese Auflösung wird wegen der höheren Farbdynamik im Studiobereich genutzt. Die Gammakorrektur von R′G′B′ wirkt sich nur auf das Helligkeitssignal Y′ aus. Die Schreibweise sollte deshalb korrekterweise Y′CbCr statt YCbCr sein.

Die folgenden Gleichungen zeigen die allgemeine Berechnung der Y′PbPr-Wertetripel, ohne zunächst einen Bezug auf einen bestimmten Standard zu nehmen:

${\begin{matrix}{}Y'&=&Kr\cdot R'+(1-Kr-Kb)\cdot G'+Kb\cdot B'\\Pb&=&0{,}5\cdot \displaystyle {{B'-Y'} \over {1-Kb}}\\Pr&=&0{,}5\cdot \displaystyle {{R'-Y'} \over {1-Kr}}\end{matrix}}$

Die dabei auftretenden Konstanten Kr und Kb sind in der ITU-R BT 601 (ehemals CCIR 601) für Fernsehen in der Standardauflösung SDTV definiert.

Somit sind sie von diesem Standard abhängig und mit Kb = 0,114 und Kr = 0,299 festgelegt. Die Wahl dieser Koeffizienten ist aus den Darstellungseigenschaften der Kathodenstrahlröhre bestimmt. Als ITU-R-B.601-konforme Umrechnung für Y'PbPr-Werte ergeben sich die folgenden Formeln.

${\begin{bmatrix}Y'\\Pb\\Pr\end{bmatrix}}\approx {\begin{bmatrix}0{,}299&0{,}587&0{,}114\\-0{,}168736&-0{,}331264&0{,}5\\0{,}5&-0{,}418688&-0{,}081312\end{bmatrix}}\cdot {\begin{bmatrix}R'\\G'\\B'\end{bmatrix}}$

Diese Werte werden mit einer gewollten Auflösung digitalisiert und mit einem Offset versehen zu YCbCr-Werte umgerechnet. Der Offset ist notwendig, um bei digitalen Videodaten reservierte Werte wie 0 und 255 für spezielle Steueraufgaben (Synchronisation) frei zu halten. Die Werte im Bereich „Reserve oben“ oder „Reserve unten“ sind für die Übersteuerung der Videosignale reserviert und sollten nicht verwendet werden.

In der folgenden Übersicht ist die Digitalisierung für eine 8-Bit-Dynamik gezeigt. Die untere Reserve sei {1, 2, …, 15}, die obere von {236, 237, …, 254}, die Synchronisationswerte {0, 255}. Y′ liegt somit im Wertebereich {16, 17, …, 235} und Cb und Cr in {16, 17, …, 240}:

${\begin{bmatrix}Y'\\Cb\\Cr\end{bmatrix}}\approx {\begin{bmatrix}16\\128\\128\end{bmatrix}}+{\begin{bmatrix}65{,}481&128{,}553&24{,}966\\-37{,}797&-74{,}203&112{,}0\\112{,}0&-93{,}786&-18{,}214\end{bmatrix}}\cdot {\begin{bmatrix}R'\\G'\\B'\end{bmatrix}}$

Liegen die R′G′B′-Daten bereits digital als R′_dG′_dB′_d im Wertebereich {0, 1, …, 255} vor, so erfolgt die Umrechnung für 8-Bit-Dynamik nach folgenden Formeln:

${\begin{bmatrix}Y'\\Cb\\Cr\end{bmatrix}}\approx {\begin{bmatrix}16\\128\\128\end{bmatrix}}+\displaystyle {1 \over 256}\cdot {\begin{bmatrix}65{,}738&129{,}057&25{,}064\\-37{,}945&-74{,}494&112{,}439\\112{,}439&-94{,}154&-18{,}285\end{bmatrix}}\cdot {\begin{bmatrix}R'_{d}\\G'_{d}\\B'_{d}\end{bmatrix}}$

Die geringen Abweichungen der Koeffizienten in der Matrix ergeben sich durch den Faktor 256/255. Diese Form der Umrechnung wird wie eingangs erwähnt primär bei der digitalen Darstellung der analogen PAL- in NTSC-Farbfernsehsignalen in Standardauflösung der SDTV verwendet.

Beim HDTV-Standard ITU-R BT.709 werden andere Konstanten für Kb, Kr eingesetzt, das führt zu anderen Transformationswerten. Es gilt Kb = 0,0722 und Kr = 0,2126 entsprechend den Darstellungsmöglichkeiten von LCD- und Plasmabildschirmen. Die Matrizen sind dann entsprechend zu berechnen.

Für die YCbCr Farbkonvertierung gibt es eine große Anzahl weiterer Normen. Die Norm SMPTE 240M definiert diese Konstanten mit Kb = 0,087 und Kr = 0,212. Das YCC-Farbmodell von Kodak ist auf Fotopapier optimiert.

Die YCbCr-Transformation bei JPEG und MPEG verwendet ebenfalls dieses Farbmodell. Da JPEG keine Synchronisationswerte in den Bilddatenstrom abbilden muss, kann für die Werte von YCbCr der volle Wertebereich von 8 Bit verwendet werden, also sind {Y′, Cb′, Cr′} und auch R, G und B im Wertebereich {0, 1, …, 255} möglich.

${\begin{bmatrix}Y'\\Cb\\Cr\end{bmatrix}}\approx {\begin{bmatrix}0\\128\\128\end{bmatrix}}+{\begin{bmatrix}0{,}299&0{,}587&0{,}114\\-0{,}168736&-0{,}331264&0{,}5\\0{,}5&-0{,}418688&-0{,}081312\end{bmatrix}}\cdot {\begin{bmatrix}R'_{d}\\G'_{d}\\B'_{d}\end{bmatrix}}$

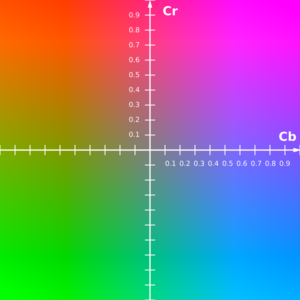
• CbCr-Flächen bei unterschiedlichem Y-Wert
• 

  Y=0

• 

  Y=0,5

• 

  Y=1

Literatur

• Charles Poynton: Digital Video and HDTV Algorithms and Interfaces. Morgan Kaufmann Publishers, San Francisco 2003. ISBN 1-55860-792-7

Weblinks

• Unterschied zwischen den verschiedenen Abtastraten bei YCbCr
  • YCbCr-Datenformate
  • [1] in englischer Sprache von Gary Sullivan und Stephen Estrop

• YCbCr 4:2:0 Streams
  • CIF
  • QCIF