Benutzer:83dot68/Draft/Kerr-Metrik

Metriken für Schwarze Löcher

	statisch $(J=0)$	rotierend $(J\neq 0)$
ungeladen $(Q=0)$	Schwarzschild-Metrik	Kerr-Metrik
geladen $(Q\neq 0)$	Reissner-Nordström-Metrik	Kerr-Newman-Metrik
$Q$: Elektrische Ladung; $\ J$: Drehimpuls

Die Kerr-Metrik ist eine Vakuumlösung der einsteinschen Feldgleichungen für ungeladene, rotierende schwarze Löcher. Sie ist nach Roy Kerr benannt, der sie 1963 veröffentlicht hat. Jeweils kurz nach der Entdeckung der Schwarzschild- bzw. Kerr-Metrik wurden auch die zugehörigen Verallgemeinerungen für den Fall von elektrisch geladenen schwarzen Löchern gefunden. Im Gegensatz zur Schwarzschild-Metrik, die auch im Außenbereich eines nichtrotierenden und sphärisch-symmetrischen Körpers beliebiger Ausdehnung gilt, beschreibt die Kerr-Metrik ausschließlich das Feld eines Schwarzen Lochs.

Linienelement

Boyer-Lindquist Koordinaten

Mit den kovarianten

$g_{tt}=-\left(1-{\frac {r_{\rm {s}}\ r}{\Sigma }}\right),\ g_{rr}={\frac {\Sigma }{\Delta }},\ g_{\theta \theta }=\Sigma ,\ g_{\phi \phi }={\frac {\chi \ \sin ^{2}\theta }{\Sigma }},\ g_{t\phi }=-{\frac {r_{\rm {s}}\ a\ r\ \sin ^{2}\theta }{\Sigma }}$

und den kontravarianten

$g^{tt}=-{\frac {\chi }{\Delta \ \Sigma }},\ g^{rr}={\frac {\Delta }{\Sigma }},\ g^{\theta \theta }={\frac {1}{\Sigma }},\ g^{\phi \phi }={\frac {\Delta -a^{2}\ \sin ^{2}\theta }{\Delta \ \Sigma \ \sin ^{2}\theta }},\ g^{t\phi }=-{\frac {r_{\rm {s}}\ a\ r}{\Delta \ \Sigma }}$

metrischen Koeffizienten, wobei

$g_{\mu \alpha }\ g^{\alpha \nu }=\delta _{\mu }^{\nu },$

lautet das Linienelement der Kerr-Raumzeit in Boyer-Lindquist-Koordinaten und geometrisierten Einheiten, d.h. $G=c=1$:

${\mathrm {d} s}^{2}=g_{\mu \nu }\mathrm {d} x^{\mu }\mathrm {d} x^{\nu }=g_{tt}\ \mathrm {d} t^{2}+g_{rr}\ \mathrm {d} r^{2}+g_{\theta \theta }\ \mathrm {d} \theta ^{2}+g_{\phi \phi }\ \mathrm {d} \phi ^{2}+2\ g_{t\phi }\ \mathrm {d} t\ \mathrm {d} \phi$

also ausgeschrieben

${\mathrm {d} s}^{2}=-\left(1-{\frac {r_{\rm {s}}\ r}{\Sigma }}\right){\rm {d}}t^{2}\ +\ {\frac {\Sigma }{\Delta }}{\rm {d}}r^{2}\ +\ \Sigma \ {\rm {d}}\theta ^{2}\ +\ {\frac {\chi \ \sin ^{2}\theta }{\Sigma }}\ {\rm {d}}\phi ^{2}\ -\ {\frac {2r_{\rm {s}}\ r\ a\ \sin ^{2}\theta }{\Sigma }}\ {\rm {d}}t\ {\rm {d}}\phi$

und der D’Alembert-Operator mit den kontravarianten Metrik-Komponenten

${\partial ^{\mu }\partial _{\mu }=g^{\mu \nu }\ {\frac {\partial }{\partial {x^{\mu }}}}\ {\frac {\partial }{\partial {x^{\nu }}}}=g^{tt}\ \left({\frac {\partial }{\partial {t}}}\right)^{2}+g^{rr}\ \left({\frac {\partial }{\partial {r}}}\right)^{2}+g^{\theta \theta }\ \left({\frac {\partial }{\partial {\theta }}}\right)^{2}+g^{\phi \phi }\ \left({\frac {\partial }{\partial {\phi }}}\right)^{2}+2\ g^{t\phi }\ {\frac {\partial }{\partial {\phi }}}{\frac {\partial }{\partial {t}}}}$

Dabei sind

$r_{\rm {s}}=2M,\quad a=J/M,\quad \Sigma =r^{2}+a^{2}\cos ^{2}\theta ,\quad \Delta =r^{2}-r_{\rm {s}}\ r+a^{2},\quad \chi =\left(a^{2}+r^{2}\right)^{2}-a^{2}\ \sin ^{2}\theta \ \Delta ,$

$M$ die Masse des felderzeugenden Körpers und $r_{\rm {s}}$ der Schwarzschild-Radius. Der Parameter $a$ wird auch Kerrparameter genannt. Er ist gemäß Definition proportional zum Drehimpuls $J$ der rotierenden Masse. Ist der Kerrparameter positiv, so führt der Körper der Masse $M$ vom Nordpol aus betrachtet eine Rotation gegen den Uhrzeigersinn aus (ein lokal drehimpulsfreier Testkörper würde dann eine positive Bewegung entlang der $\phi$-Achse ausführen), und im Fall eines negativen Kerrparameters in die entgegengesetzte Richtung.

Eigenschaften der Kerr-Metrik

Aus dem Linienelement lassen sich folgende Eigenschaften der Kerr-Metrik schließen:

• Sie ist nicht statisch, da sie nicht invariant für die Umkehrung der Zeitrichtung $t\rightarrow -t$ ist.

• Sie ist stationär, da die Komponenten des metrischen Tensors nicht von der Zeit $t$ abhängen.

• Sie ist drehsymmetrisch zur Drehachse, da die Komponenten des metrischen Tensors nicht von $\phi$ abhängen.

• Sie ist invariant gegenüber der gemeinsamen Umkehrung von $t$ und $\phi ,$

$t\ \rightarrow \ -t,\quad \phi \ \rightarrow \ -\phi ;$

diese Eigenschaft ergibt sich aus dem Umstand, dass die Umkehrung der Zeitrichtung eines rotierenden Objekts, einem in entgegengesetzter Richtung rotierenden Objekt entspricht.

• Für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r\ \rightarrow\ \infty} geht die Kerr-Metrik in die Minkowski-Metrik mit sphärischen Koordinaten über (die Kerr-Metrik ist asymptotisch flach).

• Für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a\ \rightarrow\ 0} (mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M\ \neq\ 0, \quad\Delta\ \rightarrow\ r^2\ -\ 2\ M\ r} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Sigma\ \rightarrow\ r^2} ) geht die Kerr-Metrik in die Schwarzschild-Metrik über:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{d}s^2\ \rightarrow\ -\ (1\ -\ 2\ M/r)\ {\rm d} t^2\ +\ (1\ -\ 2\ M/r)^{-1}\ {\rm d} r^2\ +\ r^2\ ({\rm d} \theta^2\ +\ \sin^2\theta\ {\rm d} \phi^2).}

• Für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M\ \rightarrow\ 0} (mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a\ \neq\ 0} ), geht die Kerr-Metrik über in

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\rm d} s^2\ \rightarrow\ -\ {\rm d} t^2\ +\ \frac{r^2\ +\ a^2\ cos^2\theta}{r^2\ +\ a^2}\ {\rm d} r^2\ +\ (r^2\ +\ a^2\cos^2\theta)\ {\rm d} \theta^2\ +\ (r^2\ +\ a^2)\ \sin^2\theta\ {\rm d} \phi^2.}

Das ist die Minkowski-Metrik der flachen Raumzeit

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\rm d} s^2\ =\ -\ {\rm d} t^2\ +\ {\rm d} x^2\ +\ {\rm d} y^2\ +\ {\rm d} z^2,}

mit den elliptischen Koordinaten

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x\ =\ \sqrt{r^2\ +\ a^2}\ \sin\theta\cos\phi}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y\ =\ \sqrt{r^2\ +\ a^2}\ \sin\theta\sin\phi}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z\ =\ r\ \cos\theta.}

Kerr-Schild Koordinaten

Um die Koordinatensingularität am Ereignishorizont zu vermeiden kann in Kerr-Schild-Koordinaten transformiert werden. In diesen lautet das Linienelement

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\rm d}s^2={\rm d}x^2+{\rm d}y^2+{\rm d}z^2-{\rm d}\hat t^2+\frac{r_{\rm s} \ r^3}{ r^4+a^2 \ z^2} \ \left({\rm d}\hat t+\frac{ r \ (x \ {\rm d}x+y \ {\rm d}y)}{ r^2+a^2}+\frac{a \ (y \ {\rm d}x-x \ {\rm d}y)}{ r^2+a^2}+\frac{z \ {\rm d}z}{ r}\right)^2}

mit der Koordinatenzeit

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat t=t+r_{\rm s} \int \frac{ r \ {\rm d} r}{\Delta} \ , \ \ {\rm d} \hat t={\rm d} t+r_{\rm s} \ {\rm d} r \ r/\Delta}

dem Azimuthalwinkel

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat \varphi=\phi+a \ \int \frac{{\rm d} r}{\Delta} \ , \ \ {\rm d} \hat \varphi={\rm d} \phi+ {\rm d} r \ a/ \Delta }

und der Transformationsregel

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x = (r \ \cos \hat \varphi + a \ \sin \ \hat \varphi) \ \sin \theta \ , \ \ y = (r \ \sin \hat \varphi - a \ \cos \ \hat \varphi) \ \sin \theta \ , \ \ z = r \cos\theta}

sowie der radialen Koordinate

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r=\sqrt{\frac{x^2+y^2+z^2-a^2+\sqrt{\left(a^2-x^2-y^2-z^2\right)^2+4 \ a^2 \ z^2}}{2}}}

Diese Koordinaten wurden von Roy Kerr in seiner originalen Arbeit von 1963 verwendet. Mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a=0} reduziert sich das Linienelement auf das Schwarzschild-Linienelement in erweiterten Eddington-Finkelstein-Koordinaten.

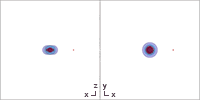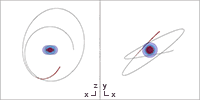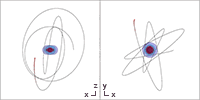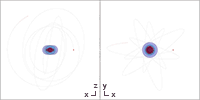
Besondere Flächen

Horizonte

Geometrische Darstellung der Ereignishorizonte und Ergosphären der Kerr-Raumzeit in kartesischen Hintergrundkoordinaten. Die Ringsingularität liegt an der äquatorialen Ausbuchtung der inneren Ergosphäre bei R=a.

In Boyer-Lindquist-Koordinaten entartet die Kerr-Metrik auf mehreren Flächen. Mit den Bezeichnungen von oben kann beispielsweise der Nenner der rein radialen Komponente der Kerr-Metrik Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_{rr}} gleich Null werden, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta = 0} gilt.

Diese Bedingung wird genau dann erfüllt, wenn

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r\ =\ r_{\text{H}}^{\pm}\ =\ M\ \pm\ \sqrt{M^2\ -\ a^2}. }

Bei maximaler Rotation mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a=M} fallen beide Werte mit dem Gravitationsradius Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_{G}=M} zusammen. Bei minimaler Rotation mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a=0} fällt der positive Wert mit dem Schwarzschild-Radius Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_s} zusammen und der negative Wert fällt auf das Zentrum. Deshalb werden diese beiden Flächen auch als innerer und äußerer Ereignishorizont bezeichnet. Obwohl die radiale Koordinate Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r} bei beiden Ereignishorizonten einen konstanten Wert besitzt, zeigt das Krümmungsverhalten der Ereignishorizonte, dass diese eher die geometrischen Eigenschaften eines Rotationsellipsoids besitzen. Der innere Ereignishorizont, bei dem es sich um einen Cauchy-Horizont handelt, entzieht sich so lange der Spinparameter Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a\leq M} der direkten Beobachtung.. Da die Raumzeit im Inneren desselben extrem instabil ist, gilt es als eher unwahrscheinlich dass sich ein solcher bei einem realen Kollaps eines Sterns tatsächlich ausbildet.

Ergosphären

Zwei weitere Flächen ergeben sich in Boyer-Lindquist-Koordinaten aufgrund eines Vorzeichenwechsels der zeitartigen Komponente Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_{tt}} . Die Bedingung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_{tt}=0} führt hier erneut auf eine quadratische Gleichung mit den Lösungen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_{\text{E}}^{\pm} = M \pm \sqrt{M^2 - a^2 \cos^2\theta}. }

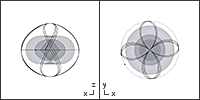
Diese zwei Flächen können wegen des Terms Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \cos^2\theta} unter der Wurzel bei geringem Spinparameter als abgeflachte Sphären, bzw. Rotationsellipsoide dargestellt werden. Die äußere Fläche berührt dabei den äußeren Ereignishorizont an den zwei Polen, die durch die Rotationsachse definiert werden. Die beiden Pole entsprechen einem Winkel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \theta} von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0} bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi} . Bei einem höheren Spinparameter beult sich die Ergosphäre von den Polen weg auch auf der z-Achse kürbisförmig aus während der innere Ereignishorizont auf den äußeren zukonvergiert und bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a=M} mit diesem zusammenfällt.

Der Raum zwischen den zwei äußeren Flächen mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r = r_{\text{H}}^\text{+}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r = r_{\text{E}}^\text{+}} wird Ergosphäre genannt. Für ein massebehaftetes Teilchen ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\rm}ds^2} mit der Metrik von Gl. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (*)} entlang seiner Weltlinie negativ. Da innerhalb der Ergospäre die Komponente Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_{tt}} der Metrik positiv ist, ist dies jedoch nur dann möglich, wenn das Teilchen mit einer gewissen mindesten Winkelgeschwindigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Omega} mit der inneren Masse Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M} mitrotiert. Es kann deshalb innerhalb der Ergosphäre keine Teilchen geben, die ruhen oder sich entgegengesetzter Richtung zu der Masse auf der Ringsingularität drehen, da die lokale Transversalgeschwindigkeit des Raumzeitstrudels (der Frame-Dragging-Effekt) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v_{\rm zamo} = \Omega \ \bar{R} \ \varsigma} ab dem äußeren Rand der Ergosphäre größer gleich der Lichtgeschwindigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} ist.

Umfangs- und Flächenformeln

Durch die nichteuklidische Geometrie ergibt sich als Umfang nicht Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U=2 \ \pi \ r} , sondern in axialer Richtung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_{\phi}=2 \ \pi \ \bar R} und in polodialer Richtung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_{\theta}=\int_0^{2 \pi } \sqrt{\Sigma } \ {\rm d}\theta} .

Deshalb ist auch die Oberfläche des Ereignishorizonts nicht Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 4 \ \pi \ r_{\text{H}}^2} sondern

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{\rm H} = \int_0^{\pi } 2 \ \pi \ \bar{R} \ \sqrt{ \Sigma } \, {\rm d} \theta = 8 \ \pi \ M \ r_{\text{H}}}

mit dem axialen Radius der Gyration

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \bar R = \sqrt{g_{\phi \phi}} = \sqrt{\frac{\chi}{\Sigma}} \ \sin \theta}

der am äußeren Ereignishorizont auf der Äquatorebene für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} mit dem Schwarzschildradius Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_{\rm s}} zusammenfällt.

Spin

Bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a > M} würde eine nackte Singularität auftreten, da der Ereignishorizont bei derartig hohen Drehimpulswerten „zerreißt“. Kip Thorne folgerte schon 1974 aus Computersimulationen des Wachstums von Schwarzen Löchern aus Akkretionsscheiben dass schwarze Löcher diesen Grenzwert nicht erreichen (seine Simulationen deuteten damals auf einen maximalen Spin von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a \approx 0{,}998 M} ). Auch Simulationen der Kollision zweier Schwarzer Löcher bei hohen Energien von 2009 von E. Berti und Kollegen zeigten, dass man dabei dem Grenzwert zwar sehr nahe kommt (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a = 0,95 M} ), er aber nicht überschritten wird, da Energie und Drehimpuls durch Gravitationswellen abgestrahlt werden.

Allgemein wird meist davon ausgegangen, dass der Grenzwert prinzipiell nicht überschritten werden kann (als Teil der Cosmic Censorship Hypothese). Diese Begrenzung für schwarze Löcher gilt jedoch nicht für Sterne und andere Objekte mit einer Ausdehnung, die signifikant größer als ihr äußerer Ereignishorizont ist. Diese müssen, bevor sie zu einem schwarzen Loch kollabieren, einen Teil ihres überschüssigen Drehimpulses nach außen abwerfen, so dass der Spin des resultierenden Schwarzen Lochs letztendlich bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a<M} liegt.

Bei einem Spinparameter von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a=M} würde der Ereignishorizont zudem mit Lichtgeschwindigkeit rotieren (siehe unten: Mitbewegte Inertialsysteme). Dieser Grenzwert wird in der Natur zwar nicht erreicht, jedoch kommen manche Schwarze Löcher, wie z.B. jenes im Kern der Spiralgalaxie NGC 1365 oder Markarian 335, sehr nahe an dieses Limit heran.

Wie bei der Schwarzschild-Metrik in Schwarzschildkoordinaten sind die Polstellen der Kerr-Metrik, welche die Lage der Ereignishorizonte beschreiben, in Boyer-Lindquist-Koordinaten ebenfalls nur Koordinaten-Singularitäten. Durch eine andere Wahl der Koordinaten kann die Raumzeit der Kerr-Metrik ebenfalls bis in das Innere der Ereignishorizonte stetig und ohne Polstellen in der Metrik beschrieben werden.

Bahn von Testkörpern

Prograde Bahn eines Testkörpers um ein rotierendes Schwarzes Loch mit a=0,9M.

Retrograde Bahn bei einem Spinparameter von a=0,95M.

Die Gleichung für die Bewegung eines Testkörpers in der Kerr Raumzeit kann über geeignete Hamilton-Jacobi Gleichungen erhalten werden. Eine für die numerische Integration geeignete Form dieser Gleichungen in Boyer-Lindquist-Koordinaten lauten in den natürlichen Einheiten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle G=M=c=1} , wobei Längen in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle GM/c^2} , Zeiten in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle GM/c^3} und der Spinparameter in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a=J c/(GM^2)} gemessen wird:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot t = \frac{2 \ E \ r \ \left(a^2+r^2\right)-2 \ a \ L_z \ r}{\Delta \ \Sigma }+E = \frac{\varsigma}{\sqrt{1-v^2}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot r = \frac{\Delta \ p_r }{\Sigma }}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot p_r = \frac{(r-1) \left(\mu \ \left(a^2+r^2\right)-k\right)+2 \ E^2 \ r \left(a^2+r^2\right)-2 \ a \ E \ L_z +\Delta \ \mu \ r}{\Delta \ \Sigma }-\frac{2 \ p_r ^2 \ (r-1)}{\Sigma }}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_r = \frac{v^{r}}{\sqrt{1+\mu \ v^2}} \sqrt{\frac{\Sigma}{\Delta}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot \theta = \frac{ p_{\theta}}{\Sigma }}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot p_{\theta} = \frac{\sin \theta \ \cos \theta \left(L_z^2/\sin ^4 \theta -a^2 \left(E ^2+\mu \right)\right)}{\Sigma }}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_{\theta} = \frac{v^{\theta} \ \sqrt{\Sigma}}{\sqrt{1+\mu \ v^2}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot \phi = \frac{2 \ a \ E \ r+ L_z \ \csc ^2 \theta \ (\Sigma -2 r)}{\Delta \ \Sigma }}

wobei der Punkt über den Variablen im Fall eines massebehafteten Testkörpers für die Differenzierung nach der Eigenzeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tau} , und im Fall eines masselosen Testteilchens nach dem affinen Parameter steht.

Dabei sind Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v^r} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v^{\theta}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v^{\phi}} die Komponenten der lokalen 3er-Geschwindigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v=\sqrt{(v^r)^2+(v^{\theta})^2+(v^{\phi})^2}=\sqrt{(v^x)^2+(v^y)^2+(v^z)^2}} entlang der jeweiligen Achsen.

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L_z} sind die erhaltene spezifische Energie, sowie die Komponente des spezifischen Drehimpulses entlang der Symmetrieachse der Raumzeit. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C} ist die nach ihrem Entdecker Brandon Carter benannte Carter Konstante:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C = p_{\theta}^{2} + \cos^{2}\theta \left( a^{2}(\mu^{2} - E^{2}) + \frac{L_z^2}{ \sin^2\theta}\right) = a^2 \ (\mu^{2}-E^2) \ \sin^2 I + L_z^2 \ \tan^2 I}

Diese gehen mit

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k = a^2 \left(E ^2+\mu \right)+ L_z ^2+C}

in die Bewegungsgleichungen ein. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_{\theta}} ist die polare Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \theta} -, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_r} die radiale Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r} - und das konstante Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_{\phi} = L_z} die azimuthale Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \phi} -Komponente des Bahndrehimpulses. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I} ist der Bahnneigungswinkel des Testteilchens. Für massebehaftete Testteilchen ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu=-1} während für masselose Teilchen wie Photonen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu=0} gilt.

Die 4 Konstanten der Bewegung sind daher Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E, L_z, C} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu} . Energie und Drehimpuls können aus den Eigenzeitableitungen der Koordinaten oder der lokalen Geschwindigkeit gewonnen werden:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E = \ -\ g_{t t}\ \dot t \ -\ g_{t \phi}\ \dot\phi = \sqrt{\frac{(\Sigma - 2 \ r) \left(\dot{\theta}^2 \ \Delta \ \Sigma +\dot{r}^2 \ \Sigma -\Delta \ \mu \right)}{\Delta \ \Sigma }+\dot{\phi}^2 \ \Delta \ \sin ^2 \theta } \ } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle = \sqrt{\frac{\Delta \ \Sigma}{(1+\mu \ v^2) \ \chi}} + \Omega \ L_z}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L_z = g_{\phi \phi} \ \dot \phi\ +\ g_{t \phi} \ \dot t = \frac{\sin ^2 \theta \ (\dot{\phi} \ \Delta \ \Sigma - 2 \ a \ E \ r)}{\Sigma -2 \ r} = \frac{v^{\phi} \ \bar R}{\sqrt{1+\mu \ v^2}}}

Mitbewegte Inertialsysteme

Korotation von lokal stationären Messbojen aufgrund des Inertial-Frame-Dragging-Effekts.

Aufgrund des Frame-dragging-Effekts korotiert selbst das Inertialsystem eines drehimpulsfreien und lokal ruhenden Beobachters (in der Literatur auch ZAMO für "zero angular momentum observer" genannt) mit der Winkelgeschwindigkeit

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Omega = -\frac{g_{t\phi}}{g_{\phi\phi}} = \frac{r_{\rm s} \ a \ r}{\chi}}

mit der sich drehenden zentralen Masse mit, wobei die Winkelgeschwindigkeit nach der Koordinatenzeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} des relativ zu den Fixsternen stationären und sich in ausreichend weiter Entfernung von der Masse befindenden Beobachters beschrieben wird.

Da der ZAMO relativ zum ihn lokal umgebenden Raum ruht nimmt die Beschreibung der lokalen physikalischen Vorgänge in seinem Bezugssystem die einfachste Gestalt an. So ist z.B. nur in seinem Bezugssystem die Geschwindigkeit eines ihn passierenden Lichtstrahls gleich 1, während sie im System eines relativ zu den Fixsternen stationären Beobachters aufgrund der gravitativen Zeitdilatation verlangsamt und aufgrund des Frame-Draggings im Betrag und in der Richtung verschoben wäre. Der ZAMO kann deshalb als lokale Messboje, relativ zu der die Geschwindigkeit vor Ort Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (v)} bestimmt wird, verwendet werden.

Die gravitative Zeitdilatation zwischen einem solchen mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Omega} mitbewegten und auf fixem Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r} sitzendem Beobachter und einem weit entfernten Beobachter beträgt

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varsigma = \frac{{\rm d}t}{{\rm d}\tau} = \sqrt{g^{t t}}} .

Die radiale lokale Fluchtgeschwindigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v_{\rm esc}} ergibt sich damit über

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varsigma = \frac{1}{\sqrt{1-v_{\rm esc}^2 }} \ \to \ v_{\rm esc}=\frac{\sqrt{\varsigma^2-1}}{\varsigma} } .

Für einen Testkörper mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E=1 \ , \ L=0} ergibt sich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v^r=v_{\rm esc}} , d.h. er entkommt der Masse mit der exakten Fluchtgeschwindigkeit.

Kreisbahnen

Pro- und retrograde Kreisbahngeschwindigkeit als Funktion von a und r

Photonenorbit auf r°_⊥=(1+√2) GM/c² bei einem lokalen Inklinationswinkel von 90° (Lz=0). Wegen der Verdrehung der Raumzeit führt das Photon trotz verschwindenem axialen Drehimpuls eine Bewegung entlang der Ф-Achse aus. Das führt dazu dass von weitem eine Bahnneigung von 61° gemessen wird.

Ein rotierendes schwarzes Loch hat 2 Radien, zwischen denen Photonenorbits aller denkbaren Inklinationswinkel möglich sind. In dieser Animation werden alle Photonenorbits für a=M gezeigt.

Die pro- und retrograde Kreisbahngeschwindigkeit (relativ zum ZAMO) ergibt sich indem

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot p_r = v^r = v^{\theta} = 0 \ , \ \ \theta=\pi/2 \ , \ \ v=v^{\phi} \ , \ \ \bar a=a/M \ , \ \ \bar r=r/M}

gesetzt und nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v^{\phi}} aufgelöst wird. Damit ergibt sich als Lösung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v^{\circ}_{+}=\frac{\bar a^2-2 \bar a \sqrt{\bar r}+\bar r^2}{\sqrt{\bar a^2+(\bar r-2) r} \left(\bar a+\bar r^{3/2}\right)}}

für die prograde und

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v^{\circ}_{-}=\frac{\bar a^2+2 \bar a \sqrt{\bar r}+\bar r^2}{\sqrt{\bar a^2+(\bar r-2) \bar r} \left(\bar a-\bar r^{3/2}\right)}}

für die retrograde Kreisbahngeschwindigkeit. Für Photonen mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v=1, \ \mu=0} ergibt sich daher

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r^{\circ}_{+}=r_{\rm s} \ \left(\cos \left(\frac{2}{3} \cos ^{-1}(-\bar a)\right)+1\right)}

für den prograden Photonenkreisradius (in Boyer-Lindquist-Koordinaten), und

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r^{\circ}_{-}=r_{\rm s} \ \left(\cos \left(\frac{2}{3} \cos ^{-1}(+ \bar a)\right)+1\right)}

für den retrograden. Für ein Photon mit verschwindendem axialen Drehimpuls, also einem lokalen Inkliniationswinkel von 90°, ergibt sich ein geschlossener Orbit auf

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r^{\circ}_{\perp}=r_{\rm s} \ \sqrt{1-\frac{\bar a^3}{3}} \cos \left(\frac{1}{3} \cos ^{-1}\left(\frac{1-\bar a^2}{\left(1-\frac{\bar a^2}{3}\right)^{3/2}}\right)\right)+\frac{r_{\rm s}}{2}}

Zwischen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r^{\circ}_{+}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r^{\circ}_{-}} sind Photonenorbits aller denkbaren Bahnneigungswinkel zwischen ±180° (retrograd) und 0° (prograd) möglich. Da alle Photonenorbits einen konstanten Boyer-Lindquist-Radius haben, kann der zum jeweiligen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r} passende Inklinationswinkel gefunden werden indem die radiale Impulsableitung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot p_r} wie oben auf 0, der initiale Breitengrad Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \theta_0} auf den Äquator gesetzt und nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v^{\phi}} aufgelöst wird.

Für Photonenorbits auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r=3M} ergibt sich außerdem für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} ein aus der Ferne beobachteter äquatorialer Inklinationswinkel von 90°. Der lokale Inklinationswinkel relativ zu einem mitrotierenden Beobachter vor Ort (ZAMO) ist höher (der axiale Drehimpuls ist dann negativ), wird aber aufgrund des Frame-Dragging-Effekts kompensiert. Im Schwarzschild-Limit mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a=0} fallen die Photonenobits aller Bahnneigungswinkel auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r^{\circ}=3M} und bilden die kugelschalenförmige Photonensphäre.

Im extremen Fall von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a=M} würden sich auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r=M} sowohl äquatoriale Photonenkreisbahnen mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v^{\circ}_{+}=1} als auch gleichzeitig Partikelkreisorbits mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v^{\circ}_{+}=1/2} ergeben. Der Grund dafür ist dass die vom Zentrum ausgehenden Kreise auf der radialen Koordinate denselben Wert einnehmen können, während sie in der euklidischen Einbettung auch einen unendlichen Abstand zueinander haben können wenn sie wie im Fall von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a=M} den gleichen lokalen Umfang Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \bar R/(2\ \pi)} einnehmen.

Literatur

• Robert H. Boyer, Richard W. Lindquist: Maximal Analytic Extension of the Kerr Metric. In: Journal of Mathematical Physics. Vol. 8, Issue 2, 1967, S. 265–281. doi:10.1063/1.1705193
• Barrett O’Neill: The geometry of Kerr black holes. Peters, Wellesley 1995, ISBN 1-56881-019-9.
• David L. Wiltshire, Matt Visser, Susan M. Scott (Hrsg.): The Kerr spacetime: Rotating Black Holes in General Relativity. Cambridge University Press, Cambridge 2009, ISBN 978-0-521-88512-6
• Roy P. Kerr: The Kerr and Kerr-Schild-Metrics. In: Wiltshire, Visser, Scott, The Kerr Spacetime, Cambridge UP 2009, S. 38–72 (Erstveröffentlichung: Discovering the Kerr and Kerr-Schild metrics. arxiv:0706.1109)

Weblinks

• Schwarze Löcher: Kerr-Metrik, Artikel von Andreas Müller in Wissenschaft-Online, August 2007
• Gravitation im Universum: Die Kerr-Lösung von Hendrik van Hees, Website des GSI Helmholtzzentrums für Schwerionenforschung