Diskussion:Banachraum
| Zum Archiv |
| Wie wird ein Archiv angelegt? |
ueblicherweise unendlich-dimensionale funktionenraeume
Banachräume sind üblicherweise unendlich-dimensionale Funktionenräume.
- Was heißt hier "üblicherweise"? ist kein Funktionenraum, und auch nicht unendlich-dimensional. Ich würde diesen Satz löschen, oder hat er einen tieferen Sinn??
- --zeno 23:06, 14. Dez 2003 (CET)
- Der Satz kann an dieser Stelle entfernt werden. Ich sehe den Sinn dieses Satzes darin, dass die in der FA betrachteten Banachraeume hauptsaechlich Funktionenraeume sind.
- Auch sollte die Definition und Eigenschaften der Lp-Raeume und lp-Raeume in einen eigenen Artikel ausgelagert werden, denn z.B. von Norm (Mathematik) wird darauf verwiesen. Nebenbei: Schreibt man die als Lp oder als Lp, oder gibts beide Schreibweisen? --SirJective 12:38, 15. Dez 2003 (CET)
- Es gibt beide.--Gunther 16:12, 26. Feb 2005 (CET)
unitaere banach-algebra
Was heisst unitäre Banach Algebra? (Algebra mit 1?) Ist unitär im Zusammenhang mit Banach-Algebren wirklich richtig? Die Erklärung unitär gibt auch keine richtige Auskunft Unyxos 00:22, 7. Jul 2004 (CEST)
- Die Reaktion kommt sehr spät, aber immerhin, sie kommt. Ich habe den beanstandeten Satz so umformuliert, dass man den Begriff "unitär" im Sinne von "hat ein Einselement" nicht kennen muss.--FerdiBf (Diskussion) 16:19, 30. Dez. 2012 (CET)
alternative definition/beispiel
Wollte erstmal andere Fachleute fragen, bevor ich diesen Satz für eine alternative Definition eines Banach-Raums in den Artikel einfüge. Also, ist folgender Satz richtig (hab ich mir hergeleitet): Ein Banach-Raum ist eine abgeschlossene Teilmenge der Menge aller stetigen komplexwertigen Funktionen auf einem kompakten Hausdorff-Raum. Mathemagier 02:54, 8. Jun 2005 (CEST)
Nachtrag: Hab gerade gesehen, dass das unter "Beispiele" schon aufgeführt ist. Das ist aber eigentlich kein Beispiel einer Art von Banach-Räumen, sondern JEDER Banach-Raum ist isometrisch isomorph zu einer geschlossenen Teilmenge..., oder? Mathemagier 02:59, 8. Jun 2005 (CEST)
'interessant'??!?
"Die interessantesten Banach-Räume sind unendlich-dimensionale Funktionenräume."- Wer legt denn bitte fest, was interessant ist und was nicht? Find ich reichlich subjektiv und sollte meiner Ansicht nach raus (sorry fuer 'IP', muss mir endlich mal nen richtigen Account zulegen) (Vorstehender nicht signierter Beitrag stammt von 87.123.21.155 (Diskussion • Beiträge) 20:25, 5. Jul 2006)
- Gemeint ist so etwas wie: die am häufigsten betrachteten Beispiele.--Gunther 20:35, 5. Jul 2006 (CEST)
- endlich dimensionale br sind isomorph zum R^n, man kann dann die ergebnisse über den R^n übernehmen. bei unendlich-dimensionalen br ist dies nicht möglich, deshalb wird hier die beweisführung schwieriger="interessanter" --84.173.166.93 21:36, 26. Jul 2006 (CEST)
- p.s. sind die l^p räume nicht auch banachalgebren wenn man die elemente komponentenweise multipliziert
- Sind sie (mit Aussnahme p gleich unendlich nicht), denn das komponentenweise Produkt von zwei Funktionen aus l^p liegt im Allgemeinen nicht in l^p UrsZH 22:02, 26. Jul 2006 (CEST)
- seien konvergiert konvergiert nach vorraussetzung --84.173.160.120 17:35, 27. Jul 2006 (CEST)
- Sind sie (mit Aussnahme p gleich unendlich nicht), denn das komponentenweise Produkt von zwei Funktionen aus l^p liegt im Allgemeinen nicht in l^p UrsZH 22:02, 26. Jul 2006 (CEST)
- p.s. sind die l^p räume nicht auch banachalgebren wenn man die elemente komponentenweise multipliziert
Verbesserungsvorschläge
Ich habe einige Verbesserungsvorschläge für diesen Artikel:
- Den Satz aus der Einleitung, in dem darauf hingewiesen wird, dass die Vollständigkeit eine Eigenschaft der Metrik ist, würde ich ersatzlos streichen. In metrischen Räumen ist diese Bemerkung zwar wichtig, aber bei isomorphen (Isomorphismus = lineare, beidseitig stetige Abbildung) normierten Räumen V und W ist V genau dann vollstängig, wenn W vollständig ist, d.h. das angedeutete Phänomen metrischer Räume tritt hier gerade nicht auf.
- Es fehlt der Begriff der Isomorphie von Banachräumen.
- Fréchet-Ableitungen sind nun wirklich nicht das erste, was man über Banachräume lernt bzw. wissen sollte. Das gehört meiner Meinung nach in einen eigenen Artikel.
- Statt der Fréchet-Ableitung sollten die drei wesentlichen Sätze (glm. Beschränktheit, offene Abbildung, Graphensatz) mit Verwesien auf die zugehörigen Artikel genannt werden.
- Ein Hinweis auf Unterräume und Quotientenräume fehlt.
- Der letzte Abschnitt über Räume differenzierbarer Funktionen und Distributionen klingt ein wenig unbeholfen, ohne damit dem Autor zu Nahe treten zu wollen. Ich würde den lokalkonvexen Raum als Verallgemeinerung des normierten Raums vorstellen und dann diese Räume als Beispiele nennen oder nur auf passende Artikel verweisen.
Über Meinungen zu diesem Diskussionsbeitrag würde ich mich freuen. Ich werde mich dann an eine Umgestaltung des Artikels machen.--FerdiBf 22:10, 4. Apr. 2008 (CEST)
- Ich hoffe, du hast den Artikel noch auf deiner Beobachtungsliste und hast noch Lust, ihn zu bearbeiten. Ich stimme dir weitgehend zu, kenne mich aber zu wenig aus, um selbst Hand anzulegen. Für mich gehören zu einem Artikel über mathematische Räume oder Strukturen immer Abschnitte zu Unterräumen und zu strukturerhaltenden Abbildungen. Die Aussage, dass Vollständigkeit eine Eigenschaft der Normtopologie ist, sollte man auch dort ergänzen.
- Die Frechet-Ableitung kann von mir aus auch drinbleiben, vielleicht gekürzt, muss aber nicht. Wenn sie drinbleibt, dann sollte sie auf jeden Fall weiter ans Ende rutschen. --Digamma (Diskussion) 20:51, 5. Jul. 2012 (CEST)
Normalerweise die reellen oder komplexen Zahlen
Ich dachte der Begriff Norm sei nur für reelle und komplexe Zahlen definiert. Wie soll man nun einen Banach-Raum über einem anderen Körper haben können? --Jobu0101 16:40, 27. Mai 2011 (CEST)
- Über bewertete Körper kann man auch eine entsprechende Theorie aufbauen (z.B. p-adische Körper), das ist aber nicht weit verbreitet und hat seltsame Eigenheiten, z.B. haben alle Banachräume über den p-adischen Körpern eine Basis (J.P. Serre). Normalerweise betrachtet man nur die die reellen oder komplexen Zahlen als Skalarenkörper.--FerdiBf 23:11, 27. Mai 2011 (CEST)
- Hat nicht jeder Vektorraum eine Basis? --Jobu0101 11:43, 28. Mai 2011 (CEST)
- Jeder Vektorraum hat eine Hamelbasis. Spricht man im Zusammenhang mit Banachräumen von Basen, so meint man in der Regel eine Schauderbasis, und das hatte ich gemeint.--FerdiBf 20:05, 28. Mai 2011 (CEST)
- Ah, okay. Herzlichen Dank. --Jobu0101 21:53, 5. Jun. 2011 (CEST)
- Jeder Vektorraum hat eine Hamelbasis. Spricht man im Zusammenhang mit Banachräumen von Basen, so meint man in der Regel eine Schauderbasis, und das hatte ich gemeint.--FerdiBf 20:05, 28. Mai 2011 (CEST)
- Hat nicht jeder Vektorraum eine Basis? --Jobu0101 11:43, 28. Mai 2011 (CEST)
Ich ändere das mal. Auch wenn man über anderen Körpern entsprechende Theorien aufbauen kann, sind das dann doch andere Theorien. Auch bei Norm und Normierter Raum ist nur von Vektorräumen über oder die Rede. --Digamma (Diskussion) 20:17, 5. Jul. 2012 (CEST)
Zwei Möglichkeiten
Der Absatz klingt so, als gäbe es bis auf unwichtige Unterschiede genau zwei Wahlmöglichkeiten. Man kann nicht immer eine explizit angebbare, vollständige Norm wählen und für unvollständige Normen hat man typischerweise eine Vielzahl an Möglichkeiten. --I217 08:59, 9. Dez. 2011 (CET)
- Ich denke, durch die Angabe, es wird eine beliebige Norm gewählt, wird deutlich, dass es mehrere mögliche Normen gibt, falls dieser Weg eingeschlagen wird. Im anderen Fall lässt sich ja der Zusatz dazuschreiben "falls eine explizit angebbare Norm existiert". --Eulenspiegel1 11:14, 9. Dez. 2011 (CET)
- Es wird auch keine beliebige Norm gewählt, sondern eine zum Problem passende. Was willst du mit dem Absatz ausdrücken, das über das Offensichtliche (ein normierter Raum kann vollständig sein oder auch nicht) und das bereits Ausformulierte (normierte Räume kann man vervollständigen) hinausgeht? --I217 11:44, 9. Dez. 2011 (CET)
- Ja, wenn man eine beliebige Norm wählen kann, dann wählt man natürlich die Norm, die am besten zum Problem passt. Das ist trivial. Das Wort beliebig drückt nicht aus, dass alle Normen gleich gut oder gleich schlecht zum Problem passen. Dass Wort beliebig drückt aus, dass es für die Möglichkeit der anschließenden Vervollständigung egal ist, welche Norm man wählt.
- In dem Absatz geht es erstmal nicht um normierte Räume sondern um nichtnormierte Vektorräume. Und der Satz drückt eben aus, dass es eben zwei Möglichkeiten gibt, so einen nichtnormierten Vektorraum zu einem Banachraum zu machen: Entweder unter Beibehaltung der Menge des Raumes. (Das funktioniert aber nicht mit allen Normen.) Oder wenn man eine andere Norm wählen will, dann über anschließende Vervollständigung. Oder anders ausgedrückt: Es hängt nicht nur von der Norm ab, ob ein Vektorraum zu einem Banachraum wird. Es ist ein Zusammenspiel von Normierung und Vervollständigung, von der es abhängt, ob ein Vektorraum zu einem Banachraum wird. --Eulenspiegel1 11:57, 9. Dez. 2011 (CET)
- Was können der Vektorraum oder die Norm dafür, wenn du sie durch einen anderen normierten Raum (nämlich durch die Vervollständigung) ersetzt? Jeder Vektorraum "wird zu" einem Banachraum, wenn man ihn durch den Nullvektorraum ersetzt. --I217 12:14, 9. Dez. 2011 (CET)
- Ich ersetze den Raum ja nicht, ich füge ihm zusätzliche Elemente hinzu. Nehmen wir als Beispiel den Raum der differenzierbaren Funktionen auf [0,1]. Nun versehen wir diesen Vektorraum mit der Supremumsnorm und vervollständigen ihn. Die differenzierbaren Funktionen bleiben erhalten. Aber zusätzlich bekommen wir auch noch alle anderen stetigen Funktionen auf [0,1] hinzu. Der Raum der stetigen Funktionen auf [0,1] (incl. Supremumsnorm) ist kein vollständig neuer Raum sondern es ist eine Erweiterung des Raumes der differenzierbaren Funktionen (incl. Supremumsnorm). --Eulenspiegel1 12:36, 9. Dez. 2011 (CET)
- Das ist wieder das bekannte Verständnisproblem: Es gibt mathematische Eigenschaften (ein normierter Raum kann vollständig sein, ein topologischer Raum kann metrisierbar sein), und es gibt Entscheidungen, die außerhalb der mathematischen Ebene statfinden (du betrachtest statt einem Raum seine Vervollständigung, du betrachtest eine Metrik auf einem vorgegebenen topologischen Raum). --I217 13:09, 9. Dez. 2011 (CET)
- Ich ersetze den Raum ja nicht, ich füge ihm zusätzliche Elemente hinzu. Nehmen wir als Beispiel den Raum der differenzierbaren Funktionen auf [0,1]. Nun versehen wir diesen Vektorraum mit der Supremumsnorm und vervollständigen ihn. Die differenzierbaren Funktionen bleiben erhalten. Aber zusätzlich bekommen wir auch noch alle anderen stetigen Funktionen auf [0,1] hinzu. Der Raum der stetigen Funktionen auf [0,1] (incl. Supremumsnorm) ist kein vollständig neuer Raum sondern es ist eine Erweiterung des Raumes der differenzierbaren Funktionen (incl. Supremumsnorm). --Eulenspiegel1 12:36, 9. Dez. 2011 (CET)
- Was können der Vektorraum oder die Norm dafür, wenn du sie durch einen anderen normierten Raum (nämlich durch die Vervollständigung) ersetzt? Jeder Vektorraum "wird zu" einem Banachraum, wenn man ihn durch den Nullvektorraum ersetzt. --I217 12:14, 9. Dez. 2011 (CET)
- Es wird auch keine beliebige Norm gewählt, sondern eine zum Problem passende. Was willst du mit dem Absatz ausdrücken, das über das Offensichtliche (ein normierter Raum kann vollständig sein oder auch nicht) und das bereits Ausformulierte (normierte Räume kann man vervollständigen) hinausgeht? --I217 11:44, 9. Dez. 2011 (CET)
Mooooment! Ich halte den ersten Absatz der Erläuterungen für unnötig, er sagt eigentlich nicht Neues. Ich habe die Definition etwas klarer formuliert. Bitte beachtet, dass bei einem normierten Raum die Norm gegeben ist (das wird nichts mehr gewählt). Man kann allerdings zu einer äquivalenten Norm übergehen und bei manchen konkreten Problemen ist das sinnvoll, um bessere Abschätzungen zu erhalten. Die Vollständigkeit hingegen ist nicht betroffen, genau das drückt der zweite Absatz der Erläuterungen aus. Ich werde den unnötigen Absatz daher entfernen.--FerdiBf 17:30, 9. Dez. 2011 (CET)
- Der Absatz richtet sich an Zweitsemester, die die Begriffe gerade erst kennenlernen und dann vielleicht denken, dass auch jede andere Norm oder zumindest jede explizit beschreibbare Norm aus einen Banach-Raum macht. Ich ergänze das bei den Beispielen. --I217 17:51, 9. Dez. 2011 (CET)
Transitive Inklusionen
Da die n Hilberträume und diese Banachräume sind ist der Pfeil vom n zu den Banachräumen entbehrlich.--DelSarto 18:22, 28. Feb. 2012 (CET)
- Entbehrlich aber sinnvoll, da man zum Beweis nicht den Umweg über Hilberträume gehen muss. Mit dem gleichen Argument könnte man den Pfeil "Prä-Hilbertraum --> lokalkonvexer Raum" streichen, zumal man in diesem Fall beim Beweis tatsächlich über den normierten Raum geht, da dort die konvexe Nullumgebung offensichtlich ist. Ich würde die Skizze so belassen, eventuell noch die topologischen Vektorräume oder die im nebenstehenden Text erwähnten Frécheträume einarbeiten, aber das muss nicht sein.--FerdiBf 21:40, 28. Feb. 2012 (CET)
- Das Entfernen beider Pfeile würde das Schema aber übersichtlicher machen, die Beweisideeen sind ja daraus nicht ersichtlich. Nach dieser Vereinfachung kann die Skizze gerne wieder erweitert werden.--DelSarto 16:54, 29. Feb. 2012 (CET)
- Ich denke nicht, dass die Skizze übersichtlicher wird, wenn man einzelne Pfeile rauslöscht. So ist der Aufbau der Skizze symmetrisch, wirft man die angesprochenen Pfeile raus, verliert die Skizze ihre Symmetrie und ist meiner Ansicht daher schwerer zu erfassen. --Christian1985 (Diskussion) 11:00, 1. Mär. 2012 (CET)
- Symmetrie ist nicht gleich Einfachheit, außerdem würde nach Streichung der Pfeile nach einer entsprechenden Drehung auch symmetrisch, wenn man das will.--DelSarto (Diskussion) 11:30, 1. Mär. 2012 (CET)
- Ich denke nicht, dass die Skizze übersichtlicher wird, wenn man einzelne Pfeile rauslöscht. So ist der Aufbau der Skizze symmetrisch, wirft man die angesprochenen Pfeile raus, verliert die Skizze ihre Symmetrie und ist meiner Ansicht daher schwerer zu erfassen. --Christian1985 (Diskussion) 11:00, 1. Mär. 2012 (CET)
- Das Entfernen beider Pfeile würde das Schema aber übersichtlicher machen, die Beweisideeen sind ja daraus nicht ersichtlich. Nach dieser Vereinfachung kann die Skizze gerne wieder erweitert werden.--DelSarto 16:54, 29. Feb. 2012 (CET)
Bild
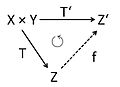
Ich habe mal wieder ein neues Bild erstellt:
Kann mir jemand sagen, in welche Kategorie das passen würde? Warum war der mit beschriftete Pfeil gestrichelt? Gibt es Änderungswünsche am neuen Bild?
Grüße, --Martin Thoma 22:00, 27. Sep. 2012 (CEST)
- Es gibt auf Commons eine Katgorie "Commutative diagrams" mit ein paar Unterkategorien.
- Die Strichelung steht normalerweise für eindeutige Existenz des Pfeils. Die nicht gestrichelten sind universell quantifiziert.
- Den Kringel in der Mitte kann man auch weglassen. Er wird mE. v.a. dazu verwendet, um beim Nach- oder Vorrechnen von irgendwelchen Dingen
- (Teil-)Diagramme als kommutativ zu markieren. In fertigen Texten beschränkt man sich darauf, überhaupt nur kommutative Diagramme hinzumalen. --Daniel5Ko (Diskussion) 00:44, 28. Sep. 2012 (CEST)
- Vielen Dank für das Feedback. Ich habs verbessert. --Martin Thoma 10:21, 28. Sep. 2012 (CEST)
Reflexivität und perfekte Paarung
Im Artikel steht, dass ein Banachraum genau dann reflexiv ist, wenn die natürliche Paarung auf perfekt ist, und mit perfekter Paarung ist jawohl eine nicht-ausgeartete gemeint (siehe Bilinearform). Das ist aber grob falsch, denn die natürliche Paarung , ist immer nicht-ausgeartet, wie aus dem Satz von Hahn-Banach folgt; das gilt sogar für alle lokalkonvexen Räume. Sollte mit Perfektheit etwas anderes gemeint sein, etwa die Bedingung aus dem Satz von James, so hätte das ausgeführt werden müssen. Dieses Kriterium findet sich auch im Artikel Reflexiver Raum, wo es hingehört. Ich werde diesen Teil daher aus diesem Artikel "Banachraum" entfernen.--FerdiBf (Diskussion) 16:07, 30. Dez. 2012 (CET)
Literaturliste
Die Literaturliste ist alles andere als repräsentativ. Die Diss von A. Willkomm aus dem Jahre 1976 über ein eher randständiges Thema scheint mir da wirklich nicht hinzugehören. We wäre es stattdessen noch mit einem Standard Buch, wie z.B. W. Rudin: Functional Analysis, Mc Graw Hill, oder Riesz/Nagy zum gleichen Thema. Nichts für ungut. --MaLeZig (Diskussion) 16:34, 17. Aug. 2014 (CEST)
- Dem stimme ich zu. In die Literatur-Liste gehört sicher auch "Lindenstrauss, Tzafriri: Classical Banach Spaces. Außerdem wäre eine alpabetische Sortierung angebracht.--FerdiBf (Diskussion) 17:07, 17. Aug. 2014 (CEST)






![{\displaystyle C[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e160d783783c799aae07cf78d250747461af0ff9)