Gruppenoperation
In der Mathematik gehört zu einer Gruppenoperation, -aktion oder -wirkung eine Gruppe als „aktiver“ Teil und eine Menge als „passiver“ Teil. Die Operation, Aktion oder Wirkung eines Elements auf der Menge ist eine Transformation (Selbstabbildung) dieser Menge. Dabei operieren die Elemente auf den Elementen der Menge in der Weise, dass die Aktion des Produkts der Hintereinanderausführung der Einzelaktionen entspricht.
Die operierende Gruppe wird Transformationsgruppe genannt. Die Menge zusammen mit der Operation von auf heißt -Menge.
Ist bei der Menge zusätzliche Struktur von Bedeutung, sei es algebraische, geometrische, topologische, wird eine Gruppenoperation nur dann als zulässig erachtet, wenn sie diese Struktur bewahrt.
Die Gruppenoperation ermöglicht es in Algebra, in Geometrie und vielen anderen Bereichen der Mathematik, die Symmetrien von Objekten mit Hilfe von Symmetriegruppen zu beschreiben. Hier steht die Untersuchung der Menge, auf der die Operation wirkt, im Vordergrund. Andererseits kann die Operation einer vorgegebenen Gruppe auf geeignet gewählten Mengen in der Gruppentheorie wichtige Informationen über die Struktur der operierenden Gruppe liefern. In diesem Fall steht die Untersuchung der operierenden Gruppe im Vordergrund.
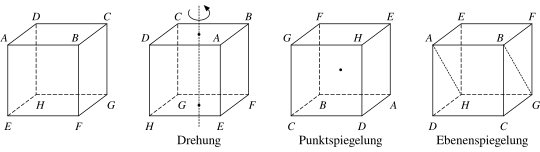
Einführendes Beispiel: Würfelgruppe und Raumdiagonalen
seien die Ecken eines Würfels in der üblichen Bezeichnung, d. h., und sind gegenüberliegende Flächen (siehe erstes Bild). Die Drehung des Würfels um die Achse, die die Mittelpunkte dieser beiden Flächen verbindet (zweites Bild), induziert die folgende Vertauschung der Ecken:
- und gleichzeitig
Durch die Drehung werden auch (gleichzeitig) die 4 Raumdiagonalen vertauscht, nämlich
Eine weitere Symmetrieabbildung, die Spiegelung an der Ebene (viertes Bild), lässt die 2 Raumdiagonalen und fest und vertauscht die anderen 2
- und
Es gibt aber auch Symmetrieabbildungen des Würfels, die die Raumdiagonalen nicht untereinander vertauschen, nämlich die Punktspiegelung am Mittelpunkt (drittes Bild): Sie entspricht
- und gleichzeitig
- und gleichzeitig
- und gleichzeitig
Dabei wird jede einzelne Raumdiagonale wenn auch gespiegelt, so doch auf sich selbst abgebildet.
Man sagt: Die Gruppe der Symmetrieabbildungen des Würfels (genannt die „Würfelgruppe“) operiert auf der Menge der Ecken, auf der Menge der Kanten, auf der Menge der Raumdiagonalen etc. Um diese Gruppe zu erfassen, werde im Folgenden der Fokus auf die Permutationen der Raumdiagonalen gerichtet.
Es gibt nun zu jedem Paar von Raumdiagonalen eine Ebenenspiegelung (in der Abbildung zum Paar und ), die diese beiden vertauscht und alle anderen Raumdiagonalen fest lässt, nämlich die Spiegelung an derjenigen Ebene, die die festbleibenden Raumdiagonalen enthält. Eine solche paarige Vertauschung heißt Transposition, und diese Transpositionen erzeugen die ganze symmetrische Gruppe der Permutationen der (vier) Raumdiagonalen. Da es dieser Permutationen gibt und genau zwei Symmetrieabbildungen, die alle Raumdiagonalen festlassen (nämlich die Identität und die oben genannte Punktspiegelung), kann man schließen, dass es insgesamt
Symmetrieabbildungen des Würfels gibt, ohne jede von ihnen einzeln zu kennen. (Für eine genauere Analyse der Gruppenstruktur siehe Oktaedergruppe.)
Definition
(Links-)Aktion
Eine (Links-)Operation, (Links-)Aktion oder (Links-)Wirkung einer Gruppe auf einer Menge ist eine äußere zweistellige Verknüpfung
mit folgenden Eigenschaften:
- für alle , wobei das neutrale Element von ist („Identität“),
- für alle („Verträglichkeit“).
Man sagt dann, operiert (von links) auf , und nennt zusammen mit dieser Gruppenoperation eine (linke) -Menge.
Aus den beiden Forderungen folgt, dass für jedes die Transformation eine bijektive Abbildung ist (die Umkehrabbildung ist ). Deswegen ist die Aktion eines Gruppenelements nicht nur eine Selbstabbildung, sondern eine Permutation von , und eine Gruppenoperation von auf kann mit einem Gruppenhomomorphismus von in die symmetrische Gruppe gleichgesetzt werden.
Rechtsaktion
Analog zur Linksoperation ist eine Rechtsoperation, -aktion oder -wirkung eine äußere zweistellige Verknüpfung
mit
- für alle und das neutrale Element von
- für alle
Der Unterschied zwischen Links- und Rechtsoperationen liegt in der Art und Weise, wie Verknüpfungen auf operieren. Bei einer Linksoperation operiert zuerst und dann , während bei einer Rechtsoperation die Reihenfolge umgekehrt ist.
Aus einer Rechtsoperation lässt sich eine Linksoperation konstruieren, indem man die Operation als Linksoperation der Gegengruppe schreibt, oder auch, indem statt von links von rechts operiert. Zu jeder Rechtsoperation gibt es eine Linksoperation
denn
und
Analog lässt sich eine Links- in eine Rechtsoperation umwandeln. Da sich Links- und Rechtsoperation im Wesentlichen nicht unterscheiden, werden ab hier nur noch Linksoperationen betrachtet.
Weitere Begriffe
Bahn
Es sei die (Links-)Operation einer Gruppe auf einer Menge Für jedes nennt man dann
die Bahn, das Transitivitätsgebiet, das Transitivitätssystem oder den Orbit (engl. orbit) von Die Bahnen bilden eine Partition von Die Anzahl der Elemente einer Bahn (bzw. ihre Mächtigkeit) wird auch die Länge der Bahn genannt. Für ein fest gewähltes nennt man die durch
gegebene Abbildung die „Orbitabbildung“.
Die Bahnen sind die Äquivalenzklassen bezüglich der Äquivalenzrelation:
falls es ein gibt, für das gilt.
Die Menge der Äquivalenzklassen wird Bahnenraum oder Orbitraum genannt.
Für eine Rechtsoperation definiert man analog
und
Fundamentalbereich
Seien ein topologischer Raum und eine Transformationsgruppe von . Für einen Punkt bezeichne die Bahn von . Dann heißt die Menge ein Fundamentalbereich von , wenn der Schnitt für jedes eine einelementige Menge ist.[1]
- Beispiel
Das Quadrat ist ein Fundamentalbereich von bezüglich der Transformationsgruppe . Jeder Punkt lässt sich schreiben als mit und .
Transitive und scharf transitive Operationen
Man bezeichnet die Gruppenoperation von auf als (einfach) transitiv oder sagt „die Gruppe operiert (einfach) transitiv auf “, wenn es zu je zwei Elementen ein gibt, so dass gilt. In diesem Fall gibt es nur eine einzige Bahn, die ganz umfasst. Ist das Gruppenelement mit darüber hinaus durch zwei beliebige Elemente eindeutig bestimmt, so nennt man die Gruppenoperation scharf (einfach) transitiv.
Gibt es sogar zu jedem Paar von Urbildern mit und jedem Paar von Bildern mit ein Gruppenelement , für das und ist, dann nennt man die Gruppenoperation zweifach transitiv und scharf zweifach transitiv, wenn es stets genau ein Gruppenelement mit der genannten Eigenschaft gibt.
Wenn Missverständnisse nicht zu befürchten sind, kann anstelle der Formulierung „die Symmetriegruppe des Graphen operiert transitiv auf den Kanten“ auch die kürzere „der Graph ist kantentransitiv“ oder „die Gruppe ist kantentransitiv“ (engl. edge-transitive) vorkommen.
Allgemein bestimmt eine Operation der Gruppe auf für stets eine Operation
auf den geordneten Teilmengen von mit Elementen (k-Tupel mit paarweise verschiedenen Komponenten) durch
Ist (scharf) einfach transitiv, dann heißt die Gruppenoperation (scharf) -fach transitiv. Mit anderen Worten: Die Gruppe operiert via genau dann -fach transitiv auf wenn bezüglich nur eine Bahn (nämlich selbst) hat, scharf -fach transitiv, wenn es für Elemente (k-Tupel) dieser Bahn stets genau ein Gruppenelement mit gibt. Wichtige Anwendungen haben solche (scharf) transitiven Operationen in der Geometrie, siehe zum Beispiel Affinität (Mathematik), Moufangebene, Affine Translationsebene.
- Beispiele
- Die Vierergruppe operiert (scharf einfach) transitiv auf der Menge , da die Ziffer 1 in jede andere übergeführt werden kann. Das gilt nicht für die Vierergruppe , die isomorph zu ist.
- Die Galoisgruppe eines über irreduziblen Polynoms mit rationalen Koeffizienten operiert transitiv auf der Menge der Nullstellen des Polynoms.[2]
Intransitive Permutationsgruppe
Hat die Gruppenoperation mehr als eine Bahn, nennt man sie intransitiv. Diejenigen Permutationen einer intransitiven Permutationsgruppe, die nur die Ziffern einer Bahn vertauschen, die übrigen Ziffern ungeändert lassen, bilden eine Untergruppe, die transitiv wird, wenn man die ungeänderten Ziffern weglässt.
Homogene Operationen
Eine Verallgemeinerung der -fach transitiven Operation ist die -fach homogene Operation. Eine Gruppe operiert -fach homogen auf der Menge mit wenn es für zwei beliebige Teilmengen mit je genau Elementen stets mindestens ein Gruppenelement gibt, das auf abbildet, also mit Jede -fach transitive Operation ist auch -fach homogen. Von der homogenen Operation wird im Unterschied zur transitiven Operation nicht verlangt, dass die vorgegebenen Urbildelemente in einer bestimmten Reihenfolge auf die vorgegebenen Bildelemente abgebildet werden.
Stabilisator
Für ein nennt man
den Stabilisator, die Isotropiegruppe, die Fixgruppe oder die Standuntergruppe von ist eine Untergruppe von , die auf operiert. Durch die Operation ist dann eine kanonische Bijektion zwischen dem Bahnenraum (Nebenklassen, siehe unten) des Stabilisators und der Bahn von gegeben:
operiert (durch Einschränkung von ) auf Ist diese Operation -fach transitiv und so ist die Operation von auf sogar -fach transitiv.
Ist eine Teilmenge und eine Untergruppe, und gilt
- mit
so sagt man, dass stabil unter ist oder dass von stabilisiert wird. Es gilt dann stets sogar Der Stabilisator eines Punktes ist also die maximale Untergruppe von die stabilisiert.
Freie und treue Operationen
Die Operation heißt frei, falls jedes Element der Menge nur vom neutralen Element der Gruppe fixiert wird. Das bedeutet, dass sämtliche Stabilisatoren trivial sind, d. h. für alle
Die Operation heißt treu bzw. effektiv, falls nur das neutrale Element der Gruppe alle Elemente der Menge fixiert. Das bedeutet, dass der zugehörige Homomorphismus trivialen Kern hat, also injektiv ist. Für treue Operationen kann als Untergruppe von aufgefasst werden. Für treue Operationen mit endlicher Menge sagt man auch: „ operiert als Permutationsgruppe auf “
Jede freie Gruppenoperation auf einer nichtleeren Menge ist treu.
Homomorphismen zwischen G-Mengen
Wenn eine weitere Menge mit einer -Linksoperation ist und eine Abbildung, so dass für alle und für alle gilt:
dann wird als G-äquivariant oder auch als Homomorphismus von -Mengen bezeichnet.
Eigenschaften
Die Äquivalenzklassen der oben eingeführten Äquivalenzrelation sind genau die Bahnen. Daraus folgt die
- Bahnengleichung: Die Mächtigkeit von ist gleich der Summe über die Länge aller Bahnen.
Genauer gilt (mit als der Fixgruppe von ) der
- Bahnensatz: Ist dann ist die Abbildung eine Bijektion.
Aus dieser Bijektion folgt für eine endliche Gruppe die Bahnformel
Insbesondere ist die Länge jeder Bahn ein Teiler der Ordnung von
Beispiele
Operation einer Gruppe auf sich selbst
Operation durch Multiplikation
Das einfachste Beispiel einer Operation ist die Operation einer Gruppe auf sich selbst: ist stets eine Operation auf , denn und
Die Abbildung ordnet jedem Gruppenelement die Linkstranslation mit diesem zu. Weil die Operation treu ist, ist ein injektiver Gruppenhomomorphismus, man erhält hieraus den
- Satz von Cayley: Jede endliche Gruppe der Ordnung ist isomorph zu einer Untergruppe der symmetrischen Gruppe
Analoges gilt auch für die Rechtstranslation
Betrachtet man eine Untergruppe von dann operiert auch auf Die Bahn eines Elements heißt dann auch Rechtsnebenklasse und Linksnebenklasse von Man beachte, dass im Allgemeinen nicht sein muss. Die Mächtigkeit der Menge aller Rechtsnebenklassen bezeichnet man mit
Da in einer Gruppe jede Rechtstranslation eine Bijektion ist, gilt für jedes Daraus folgt mit der Bahnengleichung der
- Satz von Euler-Lagrange: Für jede Untergruppe einer endlichen Gruppe gilt:
- Insbesondere ist die Ordnung von ein Teiler der Ordnung von
Man kann zeigen, dass es genauso viele Linksnebenklassen wie Rechtsnebenklassen gibt, dass also
Eine Untergruppe von heißt Normalteiler, wenn für alle gilt. Ist ein Normalteiler von dann wird durch
eine Verknüpfung auf definiert, mit der eine Gruppe ist, man nennt sie die Faktorgruppe von modulo
Operation durch Konjugation
Eine Gruppe operiert auf sich durch die Konjugation, also
Die Bahnen werden in diesem Zusammenhang als Konjugationsklassen, die Stabilisatoren als Zentralisatoren bezeichnet. Aus der Bahnformel erhält man in diesem Fall die Klassengleichung.
Die Automorphismen heißen innere Automorphismen, die Menge aller inneren Automorphismen wird mit bezeichnet.
Eine elegante Anwendung der Klassengleichung lieferte Ernst Witt mit seinem kurzen Beweis (1931) des (kleinen) Satzes von Wedderburn (1905): „Endliche Schiefkörper sind kommutativ.“
Automorphismengruppe einer Körpererweiterung
Ist eine Körpererweiterung, dann bezeichnet man mit die Gruppe aller Automorphismen von die punktweise fest lassen. Diese Gruppe operiert auf durch Jede Bahn besteht aus den in liegenden Nullstellen eines Polynoms mit Koeffizienten in das über irreduzibel ist. Elemente derselben Bahn nennt man hier konjugiert über sie haben dasselbe Minimalpolynom über
Moduln und Vektorräume
Ein -(Links-)Modul ist eine abelsche Gruppe auf der eine Gruppe (von links) operiert, derart dass zusätzlich die (Links-)Operation linksverträglich mit ist, d. h., es gilt
- für alle und alle
Die Transformationen mit bilden dann die Gruppe der Automorphismen auf und die Abbildung ist ein Gruppenisomorphismus.
Ist insbesondere die skalare Multiplikation eines Vektorraums über dem Körper dann operiert die multiplikative Gruppe auf
Kategorien
Ist allgemeiner ein Objekt einer beliebigen Kategorie, so kann eine strukturverträgliche Operation einer (abstrakten) Gruppe auf definiert werden als ein Gruppenhomomorphismus
dabei ist die Gruppe der Automorphismen von im kategorientheoretischen Sinne. Die oben genannten Operationen von Gruppen auf Mengen oder abelschen Gruppen sind Spezialfälle.
Siehe auch
- G-Raum für stetige Gruppenwirkungen
- Lemma von Burnside
Weblinks
- Gruppenoperation bei MathWorld (englisch)