Geometrische Reihe

[[Hilfe:Cache|Fehler beim Thumbnail-Erstellen]]:

Die geometrische Reihe $\sum _{k=0}^{\infty }r^{k}$ für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r=\tfrac 12} , $r={\tfrac {1}{3}}$ oder $r={\tfrac {1}{4}}$ konvergiert

Eine geometrische Reihe ist die Reihe einer geometrischen Folge. Bei einer geometrischen Folge ist der Quotient $q$ zweier benachbarter Folgenglieder konstant.

Ein Quotient $q\geq 1$ ergibt eine divergente geometrische Reihe, z. B. für $q=2$ und Startwert $1:1,1+2,1+2+4,1+2+4+8,...$ zusammengefasst also Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle 1,3,7,15,...}

Für $|q|<1$ konvergiert die geometrische Reihe hingegen; es gilt in diesem Fall

$\sum _{k=0}^{\infty }q^{k}=1+q+q^{2}+\dots ={\frac {1}{1-q}}$

mit der Festlegung $0^{0}:=1$, die im Zusammenhang mit Potenzreihen üblich ist.

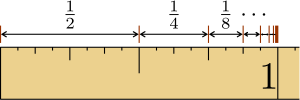
Bei identischem Startwert 1 und einem Quotienten von ¹⁄₂ ergibt sich zum Beispiel: 1, 1 + ¹⁄₂, 1 + ¹⁄₂ + ¹⁄₄, 1 + ¹⁄₂ + ¹⁄₄ + ¹⁄₈, …, also 1, ³⁄₂, ⁷⁄₄, ¹⁵⁄₈, … mit dem Grenzwert Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {\tfrac {1}{1-1/2}}=2} .

Berechnung der (endlichen) Partialsummen einer geometrischen Reihe

Eine Reihe ist per Definition eine Folge von Partialsummen. Der Wert der Reihe ist der Grenzwert dieser Folge von Partialsummen. Eine endliche Summe ist somit ein Folgenglied aus der Folge der Partialsummen. Die (endliche) Summe der ersten $n$ Glieder einer Reihe bezeichnet man also als $n$-te Partialsumme und nicht etwa als „Partialreihe“ o. ä.

Gegeben sei eine geometrische Folge $(a_{k})_{k\in \mathbb {N} _{0}}$.

Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle s=\sum _{k=0}^{\infty }a_{k}}

ist die zugehörige geometrische Reihe.

Wir können daraus eine neue Folge

$(s_{n})=\left(\sum _{k=0}^{n}a_{k}\right)=\left(\sum _{k=0}^{0}a_{k},\sum _{k=0}^{1}a_{k},\sum _{k=0}^{2}a_{k},\sum _{k=0}^{3}a_{k},\dotsc \right)=\left(a_{0},a_{0}+a_{1},a_{0}+a_{1}+a_{2},a_{0}+a_{1}+a_{2}+a_{3},\dotsc \right)$

konstruieren, deren $n$-tes Glied jeweils die Summe der ersten $n$ Glieder der Reihe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s} ist, die sogenannte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} -te Partialsumme von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s} . Diese Folge heißt die Folge der Partialsummen zu $s$. (Genau genommen wird in umgekehrter Reihenfolge die Reihe auf Grundlage von Partialsummen einer Folge definiert. Die obige und übliche Schreibweise für die Reihe gibt das aber nicht her, deshalb müssen wir aus ihr erst die Folge der Partialsummen rekonstruieren.) Falls sie konvergiert, wird über sie der Wert der Reihe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s} definiert. Es gilt für den Wert der Reihe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s} (hier wird nicht mehr von „Grenzwert“ gesprochen):

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s := \lim_{n \to \infty}s_n;}

in Worten: Der Wert der Reihe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s} ist definiert als der Grenzwert der zu ihr gehörigen Partialsummen-Folge, falls diese konvergiert, andernfalls wird die Reihe als divergent bezeichnet. Falls in diesem Falle die Folge der Partialsummen gegen (plus / minus) Unendlich strebt, schreibt man gewöhnlich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s = \lim_{n \to \infty}s_n = \infty} oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {-}\infty} und sagt, die Folge konvergiere gegen den uneigentlichen Grenzwert (plus / minus) Unendlich oder die Reihe habe den uneigentlichen Wert (plus / minus) Unendlich. (Eine Berechnungsformel für den Grenzwert folgt weiter unten.)

Mit $q$ bezeichnen wir nun das Verhältnis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{k+1}/a_{k}} zweier benachbarter Glieder, das für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} gleich ist.

Dann gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_k = a_0 q^k} für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} .

Für die Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} -te Partialsumme $s_{n}$ ergibt sich damit:

$s_{n}=a_{0}\sum _{k=0}^{n}q^{k}$

Wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q \neq 1} , dann gilt (Herleitung siehe unten)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_n = a_0\frac{q^{n+1}-1}{q-1} = a_0\frac{1-q^{n+1}}{1-q}}

Falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q=1} , so gilt

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_n = a_0 (n+1)}

Das Obige gilt, wenn die Folgenglieder Elemente eines unitären Ringes sind, also insbesondere, wenn es reelle Zahlen sind.

Verwandte Summenformel 1

Die Partialsumme

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_n=a_0\sum_{k=0}^{n} q^k k}

hat für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q \neq 1} das Ergebnis

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_n = a_0\frac{n q^{n+2}-(n+1) q^{n+1}+q}{(q-1)^2} }

und für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q = 1} (vgl. Gaußsche Summenformel)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_n = a_0 \sum_{k=0}^{n} 1^k k = a_0 \sum_{k=0}^{n} 1 k = a_0 \sum_{k=0}^{n} k = a_0 \frac{n (n+1)}{2}} ;

diese Formel ergibt sich auch aus der Formel für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q \neq 1} (mit zweifacher Anwendung der Regel von de L’Hospital) als deren Grenzwert für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q \to 1} .

Verwandte Summenformel 2

Die Partialsumme

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_n=a_0\sum_{k=0}^{n}q^k k^2}

hat für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q \neq 1} das Ergebnis

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_n=a_0\frac{n^2q^{n+3}-(2n^2+2n-1)q^{n+2}+(n+1)^2q^{n+1}-q^2-q}{(q-1)^3}}

und für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q = 1} (vgl. Potenzsummen)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_n=a_0\frac{n(n+1)(2n+1)}{6}}

Beispiele

Zahlenbeispiel

Gegeben sei die geometrische Folge

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_0=5,\ a_1=15,\ a_2=45,\ a_3=135,\ \dotsc }

mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_0=5} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q=3.} Die zugehörige geometrische Reihe ist

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s = 5 \sum_{k=0}^{\infty} 3^k = \sum_{k=0}^{\infty}5\cdot 3^k = 5+15+45+135+\dotsb = \infty}

Die zugehörige Folge von Partialsummen ergibt sich zu

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_0=5=5\frac{1-3^1}{1-3}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_1=5+15=20=5\frac{1-3^2}{1-3}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_2=5+15+45 =65=5\frac{1-3^3}{1-3}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_3=5+15+45+135 =200=5\frac{1-3^4}{1-3}}

usw.

Rentenrechnung

Angenommen, man zahlt am Anfang eines jeden Jahres 2000 € bei einer Bank ein und die Zinsen liegen bei 5 % [d. h. der Zinsfaktor ist: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1+(5/100)= 1{,}05} ]. Wie viel Geld hat man am Ende des fünften Jahres?

Das im ersten Jahr eingezahlte Geld wird fünf Jahre lang verzinst, man erhält dafür am Ende inklusive Zinseszins 2000 · 1,05⁵ €. Das im zweiten Jahr eingezahlte Geld wird nur noch vier Jahre verzinst und so weiter. Insgesamt ergibt sich dann durch die Rentenrechnung ein angesparter Betrag von

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} &2\,000 \cdot 1{,}05^5 + 2\,000 \cdot 1{,}05^4 + 2\,000 \cdot 1{,}05^3 + 2\,000 \cdot 1{,}05^2 + 2\,000 \cdot 1{,}05^1\\ &\quad= 2\,000 \cdot 1{,}05 \cdot ( 1{,}05^4 + 1{,}05^3 + 1{,}05^2 + 1{,}05^1 + 1{,}05^0)\\ &\quad= 2\,000 \cdot 1{,}05 \cdot \sum_{k=0}^{4} 1{,}05^k\\ &\quad= 2\,000 \cdot 1{,}05 \cdot \frac{1{,}05^{4+1}-1}{1{,}05-1}\\ &\quad= 2\,000 \cdot 1{,}05 \cdot \frac{1{,}05^5-1}{0{,}05}\\ &\quad= 11\,603{,}826 \end{align}}

Durch Zinsen hat sich das Kapital somit um 1603,83 € erhöht. Beim Nachrechnen von Kontoauszügen ist zu bedenken, dass im Bankenwesen nicht mathematisch gerundet wird.

Zum Vergleich: Würden nicht Jahr für Jahr je 2000 € eingezahlt, sondern gleich von Beginn an die ganzen 10000 € über 5 Jahre bei 5 % Zinsen angelegt, so wäre der Endbetrag

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 10\,000 \cdot 1{,}05^5 = 12\,762{,}8156}

also ein Kapitalertrag von 2762,82 €.

Allgemein gilt: Beträgt die Einlage am Anfang jedes Jahres Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_0} , der Zinsfaktor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q} und die Laufzeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} Jahre, dann ist der Endwert

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_0 \sum_{k=1}^{n} q^k = a_0 q \frac{q^{n}-1}{q-1}} .

Rentenrechnung mit linearer Dynamik

Zahlt man im Gegensatz zum vorigen Beispiel nicht jährlich einen festen Beitrag Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_0} , sondern ab dem 2. Jahr jedes Jahr Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d} mehr als im Vorjahr (lineare Dynamik) ein, so ist der Endwert

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} &\sum_{k=1}^n q^k (a_0+d (n-k)) = \sum_{k=1}^n(q^k(a_0+dn)-q^kdk )\\ &\qquad= \left( \sum_{k=1}^nq^k(a_0+dn) \right) - \left( \sum_{k=1}^nq^kdk \right)\\ &\qquad= (a_0+dn)\left( \sum_{k=1}^nq^k \right) - d \left( \sum_{k=1}^nq^kk \right)\\ &\qquad= (a_0+dn)\frac{q^{n+1}-q}{q-1} - d\frac{nq^{n+2}-(n+1)q^{n+1}+q}{(q-1)^2} \end{align}}

zum Beispiel mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_0=2.000}  € im ersten Jahr, jedes Jahr Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d=100}  € mehr als im Vorjahr, 5 % Zinsen (also Zinsfaktor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q=1{,}05} ) und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n=5} Jahren Laufzeit, dann ist der am Ende des 5. Jahres angesparte Betrag

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} &(2\,000+100 \cdot 5) \cdot \frac{1{,}05^{5+1}-1{,}05}{1{,}05-1} - 100 \cdot \frac{5 \cdot 1{,}05^{5+2}-(5+1) \cdot 1{,}05^{5+1}+1{,}05}{(1{,}05-1)^2} \\ &\qquad= 2\,500 \cdot \frac{0{,}29}{0{,}05} - 100 \cdot \frac{7{,}03-8{,}04+1{,}05}{0{,}0025} \\ &\qquad= 2\,500 \cdot 5{,}8 - 100 \cdot \frac{0{,}0449}{0{,}0025} \\ &\qquad= 14\,504{,}78 - 100 \cdot 17{,}97 \\ &\qquad= 12\,707{,}65 \end{align}}

wobei in diesem Beispiel nicht 10.000 €, sondern insgesamt 11.000 € eingezahlt wurden, also beträgt der Gewinn 1.707,65 €. Zahlt man statt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_0=2.000}  € im ersten Jahr nur Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_0=1.800}  € ein und lässt die anderen Faktoren gleich (sodass man wie im vorletzten Beispiel insgesamt 10.000 € einzahlt), dann ist der Endwert nur noch 11.547,27 €, das heißt zahlt man den gleichen Betrag ein, nur zu Beginn weniger, dafür später mehr, dann entgehen einem Gewinne (Opportunitätskosten).

Periodische Dezimalbrüche

Periodische Dezimalbruchentwicklungen enthalten eine geometrische Reihe, welche mit den obigen Formeln wieder in einen Bruch umgewandelt werden kann.

Beispiel 1:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} 0{,}2\overline{67} &= \frac{2}{10} + \frac{67}{1000} \cdot \sum_{k=0}^\infty (\frac{1}{100})^k = \frac{2}{10} + \frac{67}{1000} \cdot \frac{1}{1-\frac{1}{100}}\\ &= \frac{2}{10} + \frac{67}{1000} \cdot \frac{100}{99} = \frac{2}{10} + \frac{67}{990} = \frac{265}{990} = \frac{53}{198} \end{align}}

Beispiel 2:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0{,}\overline{9} = \frac{9}{10} + \frac{9}{100} + \frac{9}{1000} + \dotsb = \frac{9}{10} \cdot \sum_{k=0}^\infty (\frac{1}{10})^k = \frac{9}{10} \cdot \frac{1}{1-\frac{1}{10}} = \frac{9}{10} \cdot \frac{10}{9} = 1 }

Achilles und die Schildkröte

Ein sehr anschauliches Beispiel für die Anwendung (und sogar Herleitung des Grenzwerts) der geometrischen Reihe ist Geschichte von Achilles und der Schildkröte.

Der für seine Schnelligkeit bekannte Athlet Achilles tritt in einem Wettlauf gegen eine langsame Schildkröte an. Beide starten zum selben Zeitpunkt, aber die Schildkröte erhält anfangs einen Vorsprung von, zum Beispiel, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 100\,\text{m}} . Obwohl Achilles mit einer um den Faktor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p} , mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p > 1} , höheren Geschwindigkeit als die der Schildkröte läuft, kann er sie scheinbar niemals einholen. Denn: Sobald Achilles Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 100\,\text{m}} weit gelaufen ist, also den Punkt erreicht hat, an dem die Schildkröte gestartet ist, ist eine gewisse Zeit verstrichen. In dieser Zeit hat die Schildkröte die Strecke Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 100\,\text{m} / p} zurückgelegt. Achilles muss also die entsprechende Strecke weiterlaufen, um die Schildkröte einzuholen. Derweil hat die Schildkröte jedoch weitere Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 100\,\text{m} / p^2} zurückgelegt. Achilles hat die Schildkröte immer noch nicht eingeholt. Er läuft entsprechend weiter, muss nun allerdings feststellen, dass die Schildkröte in der Zwischenzeit abermals eine gewisse Strecke zusätzlich zurückgelegt hat; dieses Mal sind es Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 100\,\text{m} / p^3} . Dieses Spiel setzt sich unendlich oft fort.

Der Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} , an welchem Achilles die Schildkröte endlich einholen wird, ist gegeben durch die unendliche Summe

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x = 100\,\text{m} + \frac{100\,\text{m}}{p} + \frac{100\,\text{m}}{p^2} + \frac{100\,\text{m}}{p^3} + \dots = 100\,\text{m} \sum_{k=0}^{\infty} p^{-k}. }

Alternativ können wir Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} durch das Aufstellen zweier linearer Gleichungen bestimmen. Es seien

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} x_\text{S}(t) &= v\,t + 100\,\text{m}~~~\text{bzw.}\\ x_\text{A}(t) &= p\,v\,t \end{align} }

die Bewegungsgleichungen der Schildkröte bzw. von Achilles, wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v} die Geschwindigkeit der Schildkröte und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} die verstrichene Zeit ist. Wir suchen nun die Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} -Koordinate des Schnittpunkts von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_\text{S}(t)} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_\text{A}(t)} . Durch Gleichsetzen beider Gleichungen, Umformung auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} und Einsetzen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} in eine der beiden Gleichungen erhalten wir Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x = 100\,\text{m} / (1 - 1/p)} . Der Wert ist endlich; Achilles wird die Schildkröte also doch einholen. Vergleichen wir diese Lösung mit derjenigen von oben, so finden wir

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} 100\,\text{m} \sum_{k=0}^{\infty} p^{-k} = \frac{100\,\text{m}}{1-(1/p)}, ~~~\text{oder äquivalent}~~~ \sum_{k=0}^{\infty} q^{k} = \frac{1}{1-q}, \end{align} }

wobei im letzten Schritt auf beiden Seiten durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 100\,\text{m}} geteilt und die Variable Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q := 1 / p} , mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0 < q < 1} , eingeführt wurde.

Konvergenz und Wert der geometrischen Reihe

Datei:Geometrische reihe.svg

Konvergenz der geometrischen Reihe für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q = \tfrac{1}{2}}

Konvergenz der geometrischen Reihe auf der Zahlengeraden

Eine geometrische Reihe bzw. die Folge ihrer Partialsummen konvergiert genau dann, wenn der Betrag der reellen (oder komplexen) Zahl Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q} kleiner als Eins oder ihr Anfangsglied Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_0} gleich Null ist. Für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \|q\|<1} oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_0 = 0} konvergiert die zugrundeliegende geometrische Folge nämlich gegen Null:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lim_{k \to \infty}a_0 q^{k}=0} .

Nach dem Nullfolgenkriterium ist dies eine notwendige Bedingung für die Konvergenz der geometrischen Reihe. Da für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |q| > 1} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_0 \ne 0} die Grundfolge divergiert, liegt in diesem Falle somit auch Divergenz der Reihe vor.

Für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q = 1} ergibt sich die Divergenz der geometrischen Reihe aus

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{k=0}^N a_0 q^k = \sum_{k=0}^N a_0 \cdot 1 = (N + 1) \cdot a_0} ,

ein Ausdruck, der für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N \to \infty} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_0 \ne 0} divergiert.

Für den Fall Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q > 1} ergibt sich die Divergenz immer als bestimmte Divergenz (s. o.), für den Fall Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q\le -1} immer als unbestimmte Divergenz. Die geometrische Reihe konvergiert auch absolut, sofern sie auf normale Weise konvergiert.

Der Wert der Reihe im Konvergenzfall ergibt sich aus jener obenstehenden Formel für die Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} -ten Partialsummen durch Grenzwertbildung (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n \to \infty } ) für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |q|<1} zu

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{k=0}^{\infty} a_0 q^k = \lim_{n \to \infty} \sum_{k=0}^{n} a_0 q^k = \lim_{n \to \infty}a_0\frac{1-q^{n+1}}{1-q} = \frac{a_0}{1-q},}

denn es ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lim_{n \to \infty}(1-q^{n+1}) = 1.}

Die letzte Formel ist sogar in jeder Banach-Algebra gültig, solange die Norm von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q} kleiner als Eins ist; im Kontext linearer Operatoren spricht man auch von der Neumann-Reihe.

Herleitungen

Datei:Geometrische Reihe (Mathe-Song) – DorFuchs.webm

Herleitung der Formel für die Partialsummen

Die Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} -te Partialsumme der geometrischen Reihe lässt sich wie folgt berechnen:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_n = \sum_{k=0}^n a_0 q^k = a_0 + a_0 q + a_0 q^2 + \dotsb + a_0 q^n}

Vereinfacht:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_n = a_0 (1 + q + q^2 + \dotsb + q^n)}   (Gleichung 1)

Durch Multiplikation mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q} ergibt sich:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q s_n = a_0 (q + q^2 + q^3 + \dotsb + q^{n+1})}   (Gleichung 2)

Wenn man Gleichung 2 von Gleichung 1 subtrahiert, erhält man:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_n - q s_n = a_0 (1 - q^{n+1})}

Ausklammern von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_n} :

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_n (1-q) = a_0 (1 - q^{n+1}) \ }

Teilen durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (1-q)} liefert für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q \neq 1} die gesuchte Formel für die Partialsummen:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_n = a_0 {{1 - q^{n+1}} \over {1 - q}}}

Herleitung der Varianten

Mithilfe der oben angegebenen Formel lassen sich durch gliedweise Differentiation auch folgende endliche Reihen geschlossen darstellen, für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q\neq 1}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}\sum_{k=0}^{n}kq^{k}&=\sum_{k=0}^{n}q\frac{\mathrm{d}}{\mathrm{d}q}q^{k}=q\frac{\mathrm{d}}{\mathrm{d}q}\sum_{k=0}^{n}q^{k}=q\frac{\mathrm{d}}{\mathrm{d}q}\frac{1-q^{n+1}}{1-q}\\ &=\frac{nq^{n+2}-(n+1)q^{n+1}+q}{(1-q)^{2}} \end{align}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \sum_{k=0}^{n}k^{2}q^{k}&=\sum_{k=0}^{n}q\frac{\mathrm{d}}{\mathrm{d}q}q\frac{\mathrm{d}}{\mathrm{d}q}q^{k}=q\frac{\mathrm{d}}{\mathrm{d}q}q\frac{\mathrm{d}}{\mathrm{d}q}\sum_{k=0}^{n}q^{k}=q\frac{\mathrm{d}}{\mathrm{d}q}q\frac{\mathrm{d}}{\mathrm{d}q}\frac{1-q^{n+1}}{1-q}\\ &=\frac{n^{2}q^{n+3}-(2n^{2}+2n-1)q^{n+2}+(n+1)^{2}q^{n+1}-q^{2}-q}{(q-1)^{3}} \end{align}}

Für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |q|<1} konvergieren nach Grenzwertbildung der zugehörigen endlichen Reihe auch die unendlichen Reihen (folglich sind diese sogar gliedweise integrierbar):

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{k=0}^\infty k q^k = q \frac{\mathrm{d}}{\mathrm{d}q}\sum_{k=0}^\infty q^k = q \frac{\mathrm{d}}{\mathrm{d}q} \frac{1}{1-q}=\frac{q}{(1-q)^2}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{k=0}^\infty k^2 q^k = q \frac{\mathrm{d}}{\mathrm{d}q} q \frac{\mathrm{d}}{\mathrm{d}q}\sum_{k=0}^\infty q^k = q \frac{\mathrm{d}}{\mathrm{d}q} q \frac{\mathrm{d}}{\mathrm{d}q} \frac{1}{1-q}=q \frac{\mathrm{d}}{\mathrm{d}q} \frac{q}{(1-q)^2} = \frac{q(1+q)}{(1-q)^3}}

analog für höhere Potenzen.

Mittels der Euler-Polynome Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_s(q)} kann die Reihe auch für beliebige Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s} direkt angegeben werden.

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{k=0}^\infty k^s q^n = \frac{q A_s (q)}{(1-q)^{s+1}}}

Allgemein stellt diese Variante die Definition des Polylogarithmus dar.

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{k=0}^\infty k^s q^k = \text{Li}_{-s}(q)}

Siehe auch

• Die Konvergenz bzw. Divergenz der geometrischen Reihe ist die Grundlage für das Wurzelkriterium und das Quotientenkriterium.
• Geometrische Verteilung
• Arithmetische Reihe
• Harmonische Reihe

Literatur

• Albrecht Beutelspacher: Mathe-Basics zum Studienbeginn: Survival-Kit Mathematik. Springer, 2016, S. 198–199
• Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. Vieweg-Verlag, 8. Aufl. 2006, ISBN 3-528-67224-2
• George E. Andrews: The Geometric Series in Calculus. The American Mathematical Monthly, Band 105, Nr. 1 (Jan., 1998), S. 36–40 (JSTOR 2589524)
• Joscelyn A. Jarrett: Regular Polygons and the Geometric Series. The Mathematics Teacher, Band 75, Nr. 3 (März 1982), S. 258–261 (JSTOR 27962874)

Weblinks

Commons: Geometric series – Sammlung von Bildern, Videos und Audiodateien

Wikibooks: Mathe für Nicht-Freaks: Geometrische Reihe – Lern- und Lehrmaterialien

Wikibooks: Mathe für Nicht-Freaks: Geometrische Summenformel – Lern- und Lehrmaterialien

• Eric W. Weisstein: Geometric Series. In: MathWorld (englisch).
• Geometrische Folgen und Reihen auf mathematische-basteleien.de
• Unendliche geometrische Reihe, Archivlink, abgerufen am 8. März 2022