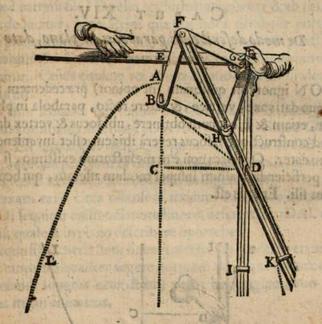
Parabelzirkel des Frans van Schooten
Der Parabelzirkel des Frans van Schooten ist ein Mechanismus, der die Form einer Parabel erzeugt. Im Jahr 1657 veröffentlichte Frans van Schooten in seinem Werk EXERCITATIONUM MATHEMATICARUM LIBRI QUINQUE[1] in LIBER IV[2] einen Parabelzirkel.[3]
Im Wesentlichen besteht der Parabelzirkel aus vier Teilen:
- einer feststehenden Hauptschiene, deren Vorderkante durch den Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E} verläuft,
- einer Raute mit den Gelenkpunkten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle BHGF,} mit der Zirkelnadel in als ersten festen Punkt der Raute,
- einem gespaltenen Diagonalstab Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |FK|,} mit dem Schreibstift in
- einer beweglichen Führungsschiene orthogonal zur Hauptschiene angeordnet, mit dem Punkt als zweiten festen Punkt der Raute.
Die Führungsschiene ist auf der Hauptschiene verschiebbar gelagert. Zusammen bilden sie einen rechten Winkel. Ein sogenannter Gleitstein, im Punkt der Führungsschiene ermöglicht eine bewegliche Verbindung des gespaltenen Diagonalstabes mit der Führungsschiene
Die Handhabung des Parabelzirkels sollen die beiden eingezeichneten Hände verdeutlichen. Nach dem Einstechen des Zirkels in den Brennpunkt hält man mit einer Hand die Hauptschiene fest. Mit der anderen Hand wird mithilfe eines Griffes im Punkt eine Dreh- und Schiebebewegung um ausgeführt. Dadurch zwingt die Führungsschiene zusammen mit dem Diagonalstab den Schreibstift in eine parabelförmige Bahn.
Eine mögliche Begründung, weshalb die mit dem Parabelzirkel des Frans van Schooten gezogenen Kurven exakte Parabeln sind, ist im nachfolgenden Abschnitt Geometrische Betrachtung beschrieben.
Geometrische Betrachtung
Zur Verdeutlichung, weshalb die mit dem Parabelzirkel erzeugten Kurven exakte Parabeln sind, wird im Folgenden zuerst in einer Basiskonstruktion ein Parabelpunkt nach Definition mit Leitlinie bestimmt und im Anschluss daran der Parabelzirkel prinzipiell eingearbeitet. In Parabel zeichnen wird dessen Bewegungsablauf erläutert. Die Bezeichnungen der Punkte sind der obigen originären Darstellung Parabelzirkel des Frans van Schooten entnommen.
Parabelpunkt nach Definition mit Leitlinie
Mit den von Bild 1 eingesetzten Bezeichnungen der Punkte, lautet eine maßgebende Aussage der Definition mit Leitlinie:
- „Eine Parabel ist der geometrische Ort aller Punkte , deren Abstand zu einem speziellen festen Punkt – dem Brennpunkt – gleich dem Abstand zu einer speziellen Geraden – der Leitlinie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l} – ist.“
Nach dem Einzeichnen der Leitlinie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l} , wird die Parabelachse gezeichnet; es ergibt den Schnittpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E} . Nun setzt man den Brennpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B} mit einem frei wählbaren Abstand zur Leitlinie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l} (je größer dieser Abstand ist, desto flacher wird die Krümmung der Parabel), z. B. unterhalb des Punktes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E} für eine nach unten offenen Parabel. Mit der gezeichneten Leitlinie und dem gewählten Brennpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B} ist die Parabel bereits mathematisch bestimmt. Die Parabel (grün) kann z. B. mithilfe einer Dynamischen‐Geometrie‐Software (DGS) eingetragen werden.
Nun zieht man mit einer abgeschätzten Zirkelöffnung jeweils einen Kreisbogen um Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B} und um den soeben auf der Leitlinie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l} entstandenen Schnittpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle G} ; die Schnittpunkte sind Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S.} Eine anschließende Gerade durch und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S} ist auch die Mittelsenkrechte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_S} des Abstandes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |BG|.} Die nun folgende Senkrechte zur Leitlinie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l} ab dem Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle G} schneidet die Mittelsenkrechte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_S} im gesuchten Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D} und bringt das gleichschenklige Dreieck
Das gleichschenklige Dreieck Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle GBD} mit
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |DB| = |DG|,}
ist eine halbe Raute, in der die Mittelsenkrechte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_S} eine Tangente der Parabel ist. Die Tangente berührt die Parabel im Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D.} Somit ist der konstruierte Punkt ein Parabelpunkt.
Konstruktion des Parabelzirkel
- Damit der Parabelzirkel eine komplette Parabellinie zeichnen kann, ist es erforderlich den Parabelpunkt (Zeichenstift) innerhalb der Raute zu legen. Anzumerken ist, in der obigen originären Darstellung Parabelzirkel des Frans van Schooten liegt außerhalb der Raute. Mit dieser Position von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D} kann nur eine gekürzte Parabellinie gezogen werden; z. B. gegen den Uhrzeigersinn, bis der Zeichenstift Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D} am Gelenkpunkt der Raute anliegt.[4]
Die nebenstehende Prinzipskizze (Bild 2) ist eine Weiterführung der Basiskonstruktion Parabelpunkt nach Definition mit Leitlinie (Bild 1). Für eine bessere Übersichtlichkeit wurde die Parabel (grün) ausgeblendet. Die hierfür erforderlichen Punkte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B, G} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D} sowie die Leitlinie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l} und die Mittelsenkrechte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_S} sind bereits bestimmt, es bedarf deshalb nur noch einer einfachen Einarbeitung der obig beschriebenen wesentlichen Teile des Parabelzirkels.
Zuerst werden die zwei Seitenlängen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \overline{FG}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \overline{GH}} der Raute, mit abgeschätzter Zirkelöffnung, größer als der Abstand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |GD|} , auf der Mittelsenkrechten festgelegt. Die Verbindung der Gelenkpunkte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F} sowie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H} schließt sich an und vollendet die Raute Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle BHGF} mit dem gleichschenkligen Dreieck Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle BGF} (hellblau). Es folgt das Einzeichnen des Diagonalstabes ab dem Gelenkpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F} über Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H} hinaus. Abschließend wird die Führungsschiene Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |GI|,} eine auf der Leitlinie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l} im Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle G} errichtete Senkrechte (Orthogonale), eingezeichnet. Sie schneidet den Diagonalstab Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |FK|} , wie vorgegeben, ebenfalls im Parabelpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D} des gleichschenkligen Dreiecks Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle GBD} (rosa).

|
Bild 3: Animierte Prinzipskizze | |
Bild 2: Prinzipskizze
|
Bild 3: Animierte Prinzipskizze
|
Parabel zeichnen
Wird der Parabelzirkel wie oben beschrieben von Hand bewegt (Bild 3), läuft der Gelenkpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle G} entlang der Leitlinie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l} und der Schreibstift (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D} ) im Spalt des Diagonalstabes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |FK|.} Die Führungsschiene Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |GI|} zwingt den Diagonalstab Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |FK|} als konstante Mittelsenkrechte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_S,} der sich kontinuierlich verändernden gleichschenkligen Dreiecke Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle GBF} und , zu wirken. Daraus folgt: In jeder gedrehten Stellung des Parabelzirkels gilt
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |DB| = |DG|.}
Damit wird aufgezeigt: Die mit dem Parabelzirkel gezogenen Kurven sind exakte Parabeln.
Anwendungen
- In der Station des Projektes Mathematik-Labor der WWU Münster,[5] wird ein stabiler und praktikabler Nachbau des Parabelzirkel von Frans van Schooten mit kleinen Abänderungen gezeigt. Mithilfe dieses realen Modells, können Schülerinnen und Schüler u. a. experimentell die Bauteile, Funktionsweise aber auch den mathematischen Hintergrund des Parabelzirkels erkunden.[6]
- Die nebenstehende Konzeptzeichnung (Bild 4) ist eine Nachempfindung dieses Nachbaus. Die Bezeichnungen der relevanten Punkte entsprechen denen im Bild 1.
- Aufbau des Nachbaus, Grundprinzip von Frans van Schooten:
- Grundplatte (hellgrau)
- Kreuzschlitten (grün)
- Schlittenführung (hellblau) mit Befestigung (anthrazit) und Anschlägen (schwarz)
- Führungsschiene (giftgrün) mit Gleitstein (schwarz)
- Raute (anthrazit)
- Diagonalstab (honigfarben)
- Anschlagschiene (ocker) mit Leitlinie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l} (blau) für das Zeichenblatt (weiß)
- Führung der Brennpunktschiene (hellblau)
- Brennpunktschiene (grau), verstellbare Schiene zum Einstellen des Brennpunktes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B.}
- Christian van Randenborgh veröffentlichte 2015 in seinem Werk Instrumente der Wissensvermittlung im Mathematikunterricht[7] einen Holznachbau aus dem Jahr 2010. Er erläutert darin den Parabelzirkel u. a. anhand der folgenden sechs, wie er sagt, „Ideen“:[8]
„Die Einsatzidee des Parabelzirkels ist das Zeichnen von Parabeln (Punkt P = Stift).
An dem Holznachbau wird ersichtlich, dass die wesentliche mechanische Idee des Parabelzirkels die Gelenkraute (FRLQ) ist.
Beim Parabelzirkel kann man die mathematische Idee in der Bau- und in der Funktionsweise wiederfinden.
Die didaktische Idee wird später noch ausführlicher erörtert werden.33
Bei einem entsprechenden Einsatz im Unterricht entsteht bei den Schülern eine Nutzungsidee, wie man mit dem Parabelzirkel zeichnen und wofür man ihn benutzen kann.
All dieses spricht dafür, dass der Parabelzirkel auch ein bestimmtes Interesse an Mathematik und einen bestimmten Blick auf die Geometrie verkörpert, kurz: eine kulturell-historische Idee in sich trägt.“
Siehe auch
Fadenkonstruktion einer Parabel
Literatur
- C. Edward Sandifer: Van Schooten's Ruler Constructions. In: Convergence. August 2010, doi:10.4169/convergence20141101 (englisch).
Einzelnachweise
- ↑ Frans van Schooten: EXERCITATIONUM MATHEMATICARUM LIBRI QUINQUE. Lugdunum Batavorum [= Leiden]: Johannes Elsevirius, 1656–1657, Inhaltsübersicht, S. 7 Online-Kopie (Google), abgerufen am 6. Februar 2019.
- ↑ Frans van Schooten: EXERCITATIONUM MATHEMATICARUM, LIBER IV. SIVE DE ORGANICA CONICARUM SECTIONUM IN PLANO DESCRIPTIONE, … Titelseite, S. 293 Online-Kopie (Google), abgerufen am 6. Februar 2019.
- ↑ Frans van Schooten: EXERCITATIONUM MATHEMATICARUM LIBER IV … Parabelzirkel, S. 356–359 Online-Kopie (Google), abgerufen am 6. Februar 2019.
- ↑ Sabine Baum: Digitale Werkzeuge. Simulationen und mathematisches Modellieren. In: Gilbert Greefrath, Hans-Stefan Siller (Hrsg.): Realitätsbezüge im Mathematikunterricht. Springer Spektrum, Wiesbaden 2018, ISBN 978-3-658-21939-0, 5.5 Mathematische Instrumente – Der Parabelzirkel, S. 104–105, Abb. 5.12 a (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 6. Februar 2019]).
- ↑ MATHEMATIK-Labor, Beschreibung des Projekts. Abgerufen am 6. Februar 2019.
- ↑ Sabine Baum: Digitale Werkzeuge. Simulationen und mathematisches Modellieren. In: Gilbert Greefrath, Hans-Stefan Siller (Hrsg.): Realitätsbezüge im Mathematikunterricht. Springer Spektrum, Wiesbaden 2018, ISBN 978-3-658-21939-0, 5.5 Mathematische Instrumente – Der Parabelzirkel, S. 105, Abb. 5.13 a (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 9. Februar 2019]).
- ↑ Christian van Randenborgh: Instrumente der Wissensvermittlung im Mathematikunterricht. Springer Spektrum, Wiesbaden 2015, ISBN 978-3-658-07290-2, 1.2.1 Der Parabelzirkel von van Schooten als Ideenkonglomerat, S. 7 ff., Abb. 1.2 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 6. Februar 2019]).
- ↑ Christian van Randenborgh: Instrumente der Wissensvermittlung im Mathematikunterricht. Springer Spektrum, Wiesbaden 2015, ISBN 978-3-658-07290-2, 1.2.1 Der Parabelzirkel von van Schooten als Ideenkonglomerat, Holznachbau aus dem Jahr 2010, S. 9 ff., Abb. 1.3 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 6. Februar 2019]).