Diskussion:Diedergruppe
Artikel neu aufgebaut
Ich habe heute den Artikel neu aufgebaut und vieles ergänzt. Kundige und geduldige Mitautoren sind wie immer willkommen! --Timofey Pnin 22:55, 1. Dez. 2009 (CET)
Probleme mit Bildern
Der Artikel enthält ein Bild, dem eine Bildbeschreibung fehlt, überprüfe bitte, ob es sinnvoll ist, diese zu ergänzen. Gerade für blinde Benutzer ist diese Information sehr wichtig. Wenn du dich auskennst, dann statte bitte das Bild mit einer aussagekräftigen Bildbeschreibung aus. Suche dazu nach der Textstelle [[Bild:diedergruppe_klein.png]] und ergänze sie.
- Wenn du eine fehlende Bildbeschreibung ergänzen willst, kannst du im Zuge der Bearbeitung folgende Punkte prüfen:
- Namensraum Datei: Bilder sollte im Namensraum Datei liegen. Bitte ändere die alten Bezeichnungen
Bild:undImage:inDatei:. - Skalierung: Außerhalb von Infoboxen sollten keine festen Bildbreiten (zum Beispiel 100px) verwendet werden. Für den Fließtext im Artikelnamensraum gibt es Thumbnails in Verbindung mit der automatischen Skalierung. Um ein Bild/eine Grafik in besonderen Fällen dennoch größer oder kleiner darzustellen, kann der „upright“-Parameter verwendet werden. Damit erfolgt eine prozentuale Skalierung, die sich an den Benutzereinstellungen orientiert. --SpBot 21:59, 1. Mär. 2009 (CET)
- Namensraum Datei: Bilder sollte im Namensraum Datei liegen. Bitte ändere die alten Bezeichnungen
Das Problem mit dem Bild ist insofern gelöst, als das Bild nicht mehr gebraucht wird. Leider kann ich jetzt ein anderes Bild noch nicht richtig aus der englischsprachigen Wikipedia importieren. Wer weiß Rat? --Timofey Pnin 22:55, 1. Dez. 2009 (CET)
Spezialfälle
Es erscheint mir sinnvoll, die Diedergruppe nur für zu definieren. Die Fälle 1 und 2 sind Trivialitäten und ihre Erklärung im Text verwirrt den Leser nur. --Hanfried.lenz 10:10, 29. Aug. 2007 (CEST)-
Insbesondere stimmt die Aussage zur Mächtigkeit der Diedergruppe für die Sonderfälle 1 und 2 nicht mehr. Es verwirrt also nicht nur, sondern macht manche Aussagen des Textes falsch. -- 79.140.39.199 22:37, 21. Apr. 2011 (CEST)
Ich habe diese Sonderfälle vorläufig weggelassen. Vielleicht kann man ihn im neuen Aufbau besser unterbringen? --Timofey Pnin 22:55, 1. Dez. 2009 (CET)
Permutationsgruppe
Der Satz:
- „Nach Durchnummerierung der Ecken kann man die Diedergruppe für n\geq 3 als Untergruppe der n-ten symmetrischen Gruppe Sn, also als Permutationsgruppe auffassen“
ist nicht aussagekräftig, da dies für jede endlich Gruppe gilt. Außerdem ist das zweite „als“ falsch. Gibt es andere Meinungen, oder soll das geändert werden?--85.178.215.217 17:36, 15. Dez. 2008 (CET)
Ich habe die Permutations-Darstellung weitgehend ausgearbeitet. Ich hoffe dieser Teil ist jetzt explizit und gut verständlich. Ergänzungen und Korrekturen sind willkommen! --Timofey Pnin 22:55, 1. Dez. 2009 (CET)
Alter Artikel brauchte Überarbeitung
Das sagt effektiv *gar nichts* aus ... Was genau ist denn nun eine Dieder-Gruppe? Eine Gruppe Zahlen? Ein Algorythmus? Ein Prüfziffersystem? --84.168.120.117 16:11, 22. Mai 2007 (CEST)
- Wer mehr als nur die erste Zeile liest wird schlauer: Symmetriegruppe, nicht, das dieser Artikel verständlicher wäre, aber das liegt weniger am Artikel als an der Komplexität des Themas.--A-4-E 16:13, 22. Mai 2007 (CEST)
Ich hoffe, jetzt ist der Artikel verständlicher und wird dem Thema gerecht. --Timofey Pnin 22:55, 1. Dez. 2009 (CET)
Stoppschild
Die zweite Zeile, welche die Spiegelungen illustrieren soll, ist falsch. Die Spiegelungen über die Seitenmitten (0, pi/4, pi/2, 3/2 pi) sind doppelt dargestellt, während die Spiegelungen durch die Eckpunkte (pi/8 usw.) fehlen. (nicht signierter Beitrag von 79.211.133.244 (Diskussion) 17:17, 3. Jun. 2010 (CEST))
- Nein, ich denke, die Abbildung ist korrekt - schließlich sind ja auch alle Bilder verschieden voneinander.
- Zuerst wird die Spiegelung an der waagerechten Diagonalen (durch die Seitenmitten) dargestellt, dann die an der Diagonale mit einem Winkel von pi/8=22,5 Grad (also duch die Ecken), dann pi/4 (nächste Seitenmitte), dann 3pi/8 usw.--Graf Alge 15:42, 22. Mär. 2011 (CET)
- Das entspricht übrigens genau der im nachfolgenden Abschnitt (Matrixdarstellung) beschriebenen Reihenfolge der Transformationen.--Graf Alge 16:01, 22. Mär. 2011 (CET)
Matrixdarstellung und Bild von D_4
In der sehr schönen anschaulichen Darstellung von D_4 stimmen leider die Lage und die Nummerierung der Eckpunkte nicht mit dem vorher im Text beschriebenen überein. Für n=4 ergäbe sich ja kein achsenparalleles Quadrat sondern eins mit den Ecken auf den Koordinatenachsen P_1=(0,1) P_2=(-1,0) P_3=(0,-1) und P_4=(1,0).
Dargestellt sind die Transformationen des umschreibenden Quadrates mit den Ecken (1,1), (-1,1), (-1,-1) und (1, -1) - das interessanter Weise dieselben Symmetrien hat. Leider sind die Ecken im Bild auch in negativer Richtung nummeriert...
Hat jemand hier eine Änderungsidee? Eine neue Zeichnung wäre vermutlich sehr aufwendig...
Eventuell kann man ganz auf die Formeln für die Koordinaten der Eckpunkte verzichten?
Welche Bedingungen müssen denn erfüllt sein, damit die Matrixdarstellungen korrekt bleiben?
Für die Drehungen sollte reichen, dass der Koordinatenursprung im Mittelpunkt des Polygons liegt, oder?
Für die Spiegelung muss zusätzlich die horizontale Achse eine Symmetrieachse sein. Reicht das?--Graf Alge 17:38, 22. Mär. 2011 (CET)
Permutationsdarstellung und Bild von D_4
Hier setzt sich das Problem mit der Eckennummerierung fort: Position und Orientierung der Nummern stimmen in Text und Abbildung nicht überein. Die Beispiel-Permutationen versuchen wohl irgendwie dem Bild gerecht zu werden, die danach folgenden allgemein gültigen Formeln beziehen sich aber (für n=4) auf das Quadrat mit den Ecken auf den Koordinatenachsen - nur dann ist eben - und nicht wie im Text zuvor behauptet usw. Was tun? Mir würde es sehr leid tun um das sehr anschauliche Bild... --Graf Alge 18:34, 22. Mär. 2011 (CET)
D2
Ich habe zwar gesehen, dass sich oben dafür ausgesprochen wurde, dies wegzulassen, D2 wird aber z.B. im Artikel Kleinsche Vierergruppe erwähnt (isomorph D2) und sollte meiner Meinung nach deshalb hier auch erwähnt werden. Das zugehörige Diagramm besteht aus zwei Zweiecken (bei D1 aus einem).--Claude J (Diskussion) 09:03, 5. Jul. 2013 (CEST)
- Habs mal ergänzt.--Claude J (Diskussion) 15:43, 5. Jul. 2013 (CEST)
n Drehungen und n Spiegelungen
Elemente, nämlich Drehungen und Spiegelungen gefällt mir nicht. Die Elementmenge wird aufgespannt durch n Drehungen (inklusive Identität) und 1 Spiegelung (exklusive Identität). Die Ordnungen sind n und 2. --Siehe-auch-Löscher (Diskussion) 09:26, 22. Nov. 2013 (CET)
- Wie wäre es mit Drehungen und Drehspiegelungen? Viele Grüße, --Quartl (Diskussion) 09:59, 22. Nov. 2013 (CET)
- Yep, ich füg das mal ein. --Siehe-auch-Löscher (Diskussion) 10:14, 22. Nov. 2013 (CET)
- Hoppla, das passt auch wieder nicht, da die Drehspiegelung laut Artikel nur im 3-dimensionalen definiert ist. Vielleicht kommen ja noch ein besserer Vorschlag. --Siehe-auch-Löscher (Diskussion) 10:37, 22. Nov. 2013 (CET)
- Hallo Siehe-auch-Löscher! Was genau gefällt Dir denn daran nicht? Es beschreibt doch nur, welcher Art die Gruppenelemente sind. Daß (wie Du schreibst) die Gruppe von n Drehungen und einer Spiegelung aufgespannt wird, ist zwar nicht falsch, gibt aber nur eine von vielen möglichen Erzeugendenmengen an. Die minimalen Erzeugendenmengen sind jedoch zweielementig: Die Gruppe wird auch von einer Drehung und einer Spiegelung aufgespannt. Die Drehung um 360°/n erzeugt einen zyklischen Normalteiler N vom Index 2 und die einzige andere Nebenklasse ist von der Form sN mit einer Spiegelung s. Bei den Elementen von N handelt es sich um n Drehungen und sN besteht aus n Spiegelungen. Genau das sagt aber das von Dir Verworfene aus. Liebe Grüße, Franz 11:05, 22. Nov. 2013 (CET)
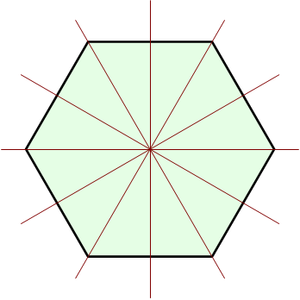
- @Siehe-auch-Löscher: vielleicht hilft dir zum Verständnis dieses Bild, bei dem die 6 Spiegelungsachsen beim regelmäßigen Sechseck gezeigt werden. (Drehspiegelungen wäre auch richtig, ist aber unnötig kompliziert). Viele Grüße, --Quartl (Diskussion) 11:28, 22. Nov. 2013 (CET)
- hat sich gekreuztJa, ich hatte gerade einen Denkfehler. Es handelt sich natürlich um n Spiegelungen an n verschiedenen Achsen. Ich bin von einer Spiegelung ausgegangen die mit der Drehung kombiniert wird. --Siehe-auch-Löscher (Diskussion) 11:32, 22. Nov. 2013 (CET)
Matrixdarstellung
Da kann meiner Ansicht nach etwas nicht stimmen. s_k wird als r_k mal s_0 (mit s_0 Spiegelung horizontale Achse, r_k drehung um ) dargestellt. Man Betrachte Quadrat. Dann ist r_k drehung um vielfaches von 90 Grad und die spiegelachsen werden dementsprechend nur um Vielfache von 90 grad gedreht, die spiegelachsen gehen aber auch durch die Ecken, mit Winkel 45 Grad.--Claude J (Diskussion) 11:41, 22. Nov. 2013 (CET)
- (Einschub nach BK): Hallo Claude! Du hast offenbar übersehen, daß die zur Spiegelung gehörende Achse nicht um den Winkel , sondern um geneigt ist. Beim Quadrat (n=4) sind das
- Liebe Grüße, Franz 12:09, 22. Nov. 2013 (CET)
- Die Spiegelungsmatrix an einer Ursprungsgerade im Winkel ist
- (man beachte den Faktor 2). Für den Winkel gilt für (maximal eine halbe Drehung), damit hat man als die Spiegelungsmatrizen
- für . Passt also. Viele Grüße, --Quartl (Diskussion) 11:57, 22. Nov. 2013 (CET)
Mir geht es um die Sätze dadrunter im Abschnitt Matrixdarstellung, insbesondere über die Zusammensetzung der Spiegelungen aus der horizontalen spiegelung und drehungen um Vielfache von 90 Grad (was auch deshalb nicht stimmen kann weil sie bei drehung um 180 grad identisch zur horizontalen spiegelung ist).--Claude J (Diskussion) 12:15, 22. Nov. 2013 (CET)
- Auch dort kann ich keinen Fehler finden. Ich verstehe aber auch nicht, was Du meinst. Kannst Du vielleicht ein ganz konkretes Beispiel angeben, wo Falsches steht?--Franz 12:45, 22. Nov. 2013 (CET) PS: Allerdings sind die einleitend angegebenen Punkte Pk (für n=4) gegenüber den Eckpunkten des Quadrates um 45° verdreht. Man sollte daher vielleicht die Koordinaten der Pk entsprechend ändern. (EDIT: Erledigt, siehe weiter oben unter Matrixdarstellung und Bild von D_4.)
Gemeint ist der Satz: " ist die Spiegelung an der horizontalen Achse und es gilt für alle ." Explizit: für k=1 entspricht das Spiegelung an vertikalere Achse, für k=2 wieder Spiegelung an horizontaler Achse und für k=3 wieder an vertikaler achse.--Claude J (Diskussion) 12:49, 22. Nov. 2013 (CET)
- (Nach BK): Bei diesem Satz handelt es sich aber um eine wahre Aussage, wie sich leicht nachrechnen läßt. Nehmen wir als Beispiel den Fall k=1, dann haben wir
- und es gilt:
- --Franz 13:04, 22. Nov. 2013 (CET)
- Zu Deinen nachträglich eingefügten Bemerkungen: Nein, die Spiegelung erfolgt für k=1 nicht an einer vertikalen, sondern an einer um 45° gegen die Horizontale geneigten Achse.--Franz 13:07, 22. Nov. 2013 (CET)
- Stimmt, seh ich jetzt auch.--Claude J (Diskussion) 13:27, 22. Nov. 2013 (CET)
Definition tatsächlich nur über Symmetrie eines n-Ecks
Ist die Diedergruppe tatsächlich nur über die Symmetrie eines regelmäßigen n-Ecks definiert? Das macht ja ab n=3 Sinn. Aber für n=1 hat man doch nur einen Punkt und bei einem Punkt hat man doch nur eine Symmetrieoperation, nämlich die Identität. Bei n=2 ist ein n-Eck eine Linie. Diese kann man um 0 Grad (Einselement) und um 180 Grad drehen, Spiegelungen gibt es aber nur eine, nämlich an der Achse senkrecht zur Linie. Eine Spiegelung an der Längsache der Linie ändert die Linie ja nicht und ist damit das Einselement. Nach meinen Überlegungen zur Symmetrie hat also D_1 ein Element und D_2 drei Elemente, was aber laut Artikel nicht stimmt. --132.230.80.150 16:49, 10. Nov. 2015 (CET)
Spezialfälle wieder
Die Behandlung der beiden Spezialfälle und muss verbessert werden, leider habe ich aber nicht die nötige Zeit. Spezifische Punkte:
- Die Erklärung des Begriffs Zweieck verstehe ich nicht.
- Der sauberste Weg, eine Fallunterscheidung für kleines zu vermeiden, ist vermutlich eine Definition über gleichverteilten Symmetrieachsen. Natürlich würde man dies als Ergänzung zur herkömmlichen Definition geben, nicht als Ersatz. Bestimmt lässt sich ein Lehrbuch finden, das diesen Zugang wählt. Dürfen auch Vorlesungsskripte als Quellen benutzt werden?
- Ich finde es hilfreich, als Isometriegruppe eines (nicht-quadratischen) Rechtecks zu betrachten.
GroupCohomologist (Diskussion) 13:21, 29. Jan. 2016 (CET)
Isometriegruppe
Aus der Einleitung: "Für ist diese Gruppe isomorph zur Isometriegruppe eines regelmäßigen Polygons in der Ebene." Spricht man da nicht eher von "Symmetriegruppe"? --Digamma (Diskussion) 13:02, 4. Mai 2020 (CEST)