Diskussion:Kugel

quadric

du dir sicher, dass quadrische Funktion die richtige Übersetzung von "quadric" ist? --Caramdir 16:26, 15. Sep 2003 (CEST)

Du hast recht, ich hätte mal den Link 'quadric' in der englischen Wikipedia anschauen sollen. Ich kenne leider keine deutsche Bezeichnung für eine solche (Hyper-)Fläche (LEO auch nicht). Aber es geht erstmal ohne den Verweis. --hh 09:55, 16. Sep 2003 (CEST)

Eine mögliche Übersetzung ist Quadrik.(Verwendung z.B in mathematik.uni-stuttgart.de --Stefanwege 21:44, 1. Sep 2004 (CEST)

Zur Einleitung

Ich finde den ersten Satz unglücklich gewählt:

Eine Kugel ist in der Mathematik ein Körper, der nur aus einer Oberfläche besteht...

Da fragt man sich: Ist es nun ein Körper (Volumen, 3-dimensional) oder eine Oberfläche (2-dimensional). Ich schlage vor:

Unter einer Kugel versteht man in der Mathematik die Fläche aller Punkte, die den gleichen Abstand von einem Punkt, dem Mittelpunkt, besitzen. Etwas weiter gefasst wird insbesondere ausserhalb der Mathematik auch der von dieser Oberfläche eingeschlossene (Fest)körper als Kugel bezeichnet.

-- Schewek 14:59, 16. Sep 2003 (CEST)

"die Fläche aller Punkte" klingt etwas seltsam. Aber, wenn man "die Menge aller Punkte" schreibt, wird die Fläche nicht erwähnt. --Caramdir 15:50, 16. Sep 2003 (CEST)

Ich würde es "die Menge aller Punkte" nennen, denn innerhalb der Mathematik besteht die "Kugeloberfläche" in höherdimensionalen Räume nicht mehr aus einer zweidimensionalen Fläche, sondern einer n-1 dimensionalen Hyperfläche. (Eine zweidimensionale Kugel hat eine Linie als Oberfläche.) Nur in unserem dreidimensionalen Raum ist die Oberfläche eine Fläche. --SirJective 13:21, 20. Dez 2003 (CET)

ich würde sagen die kugel sei ein körper, dessen oberfäche in jedem punkt stetig ist. und ich glaube die kugel ist der einzige körper für den dies gilt. bzw rotationselypsoide und der gleichen, aber bei der kugel ist der anstieg in jedem punkt gleich.

machen wirs doch einfach, eine kugel ist die summe aller punkte um einen punkt p mit einem abstand von höchstens n

Vollkugel/Hohlkugel

Auch in der Mathematik gibt es Kugeln, die nicht hohl sind. Im englischen unterscheidet man zwischen ball und sphere. Das erklaert auch die Bezeichnung Sⁿ fuer die n-dimensionale Hohlkugel, B fuer offene Vollkugeln (Inneres ohne Rand) und ${\overline {B}}$ fuer abgeschlossene Vollkugeln (mit Rand).

Im Deutschen kann der Begriff Kugel je nach Kontext das eine oder andere bedeuten: Entweder Vollkugel oder Hohlkugel (Sphäre). Diese Begriffsverwirrung sollte man noch entwirren, wie es z.B. bei Ordnungsrelation mit Halbordnung/Ordnung/totale Ordnung geschehen ist.

Im Kontext metrischer Raeume verwende ich Kugel und Sphaere, gehts dagegen um Geometrie, verwende ich Vollkugel und Kugel. --SirJective 14:30, 11. Feb 2004 (CET)

Also ich hab mal im Handbuch der Mathematik(Entspricht Kleine Enzeklopädie Mathematik),ISBN 3-7042-6019-3 nachgesehen Dort heißt es (Seite 204): " Die Kugelfläche ist der geometriche Ort aller Punkte des Raumes, die von einem festen Punkt dieses Raumes einen konstanten Abstand haben." und "Der von der Kugelfläche vollständig abgeschlossene Teil des Raumes heißt Kugel". Also: Kugel=Vollkugel Kugelfläche=Hohlkugel --Stefanwege 20:39, 1. Sep 2004 (CEST)

Ich hab auch noch mal ins Netz geschaut und die in der Tabelle unten stehenden Quelle zusammengetragen. Die Quellen sagen das Kugel Volumen und Oberflächen haben. Das haben aber nur 3-dimensionale Körper also die Vollkugel. 2-dimensionale Körper dagegen haben kein Volumen sondern eine Fläche. Auch wenn es einige Quellen gibt die Kugel im Sinne von Hohlkugel verstehen, denke ich das die seriöseren Quellen für Vollkugel stehen. --Stefanwege 21:38, 1. Sep 2004 (CEST)

Fakt	Quelle
Kugel hat Volumen	klassenarbeiten.net,uni-bayreuth.de, didmath.ewf.uni-erlangen.de
Kugel hat Oberfläche	klassenarbeiten.net, fersch.de, chemlin.de
Kugel hat Fläche	?
Kugel meint Hohlkugel	mathe-aufgaben.de, mathematik.uni-stuttgart.de, chello.at
Kugel meint Vollkugel	Spektrum der Wiss. Sept/04 Seite 90, math.ethz.ch, tu-berlin.de, Handbuch der Mathematik, ISBN 3-7042-6019-3

Eine Argumentation für die Notwendigkeit von Faktentabellen siehe hier

Nach meinen Recherchen werden die Begriffe in der Literatur häufiger im folgenden Sinn verwendet:
Kugel: Abstand zum Mittelpunkt <= r
Sphäre: Abstand zum Mittelpunkt = r
Diese Festlegung wäre auch konsistent zum Artikel Sphäre (Mathematik). Der gegenwärtige Zustand der Seite ist unbefriedigend, weil die Begriffe im einleitenden Abschnitt und bei der Verallgemeinerung in verschiedenem Sinn gebraucht werden. Wfstb 18:30, 28. Jan 2005 (CET)

Eine Hohlkugel hat zwei Oberflächen, eine innere und eine äußere. Zwischen beiden besteht (normalerweise) ein Abstand.

Stop der (Begriffsklärung typ 2) ohne Diskussion

Salve Head, es wäre sachlicher, konstruktiver wenn wir uns erst über eine Systematik der Begriffsklärungen einigen und NICHT subjektiv diese nach typ 2 subjektiv im Alleingang einzufügen. (BTW, in der Kugel_(Begriffsklärung) sollte unter Punkt 1. mathematisch stehen). Bei diesem Begriff, der der ursprüngliche ist hätte ich nichts gegen Typ2, aber NUR, wenn wir uns mehrheitlich für eine Lösung aussprechen - siehe Diskussion:Droge und Mailingliste. Wobei ich persönlich sehr dagegen wäre, wenn für Typ2 Popularität oder Quantität zählen würde. Gruss Rob 18:02, 16. Feb 2004 (CET)

Meine Güte, du kannst doch nicht über alles abstimmen! --Head 20:42, 16. Feb 2004 (CET)

Ich will nicht über alles eine Abstimmung sondern nur eine Einigung, wann Typ2 verwendet wird siehe Diskussion:Droge, dies wird bei BKL Typ 1,2,3 das Konfliktpotetial bei unserer gemeinsamen Arbeit nehmen. Und das ist kein Scheiß Gruss Rob 22:49, 16. Feb 2004 (CET)

Physik

Mathematische und physikalische Eigenschaften hängen eng zusammen. Unter "Begriffsklärung" ist "Kugel (Physik)" nicht vorhanden. Ich habe erst mal provisorisch das im mathematischen Teil mit erwähnt. Es muss entweder einen eigenen Artikel bekommen oder noch ausgebaut werden. --Hutschi 13:12, 20. Sep 2005 (CEST)

Physik

"In der Physik kommen dazu noch Impuls, Drehimpuls und Materialeigenschaften wie Masse, Elastizität, Leitfähigkeit, Lichtbrechung." Was bitte haben diese Begriffe mit "Kugel" zu tun?? Jeder beliebige Körper hat irgend einen Wert jeder dieser Größen. Autor, bitte erkläre (oder streiche).... UvM 25.12.05

Oberfläche

Bei den Formeln zur Kugel hat Benutzer:84.143.41.134 die Oberfläche ergänzt.

$A_{O}\,={\frac {dV}{dr}}$

Die Formel ist sicher mathematisch richtig, ich kann den Sinn aber nicht ganz verstehen. Ich bin für streichen.-- Petflo2000 17:18, 2. Apr 2006 (CEST)

Stelle dir zwei Kugeln mit annähernd gleichem Radius und gleichem Mittelpunkt vor. Die Differenz der beiden Kugeln - also die recht dünne Schale - wird durch die Dicke der Schale geteilt. Damit erhält man annähernd die Oberfläche der Schale. Um jedoch die genaue Oberfläche der Kugel/Sphäre zu erhalten, lässt man die Dicke der Schale, also den Unterschied der Radien r und x gegen Null gehen. Eine andere Schreibweise ist: $A_{O}=lim_{x\rightarrow r}{\frac {V(x)-V(r)}{x-r}}$ Ich würde diese Formel - eventuell näher erklärt - sehr gerne in dem Artikel sehen. --Borlox 20:18, 16. Jan. 2007 (CET)

Meiner Meinung nach macht diese Formel wenig Sinn. Dieser Zusammenhang ist natürlich nicht zufällig - wie oben schon erklärt - aber ganz sicher nicht allgemeingültig. Nimmt man z.B. das Volumen eines Würfels mit der Kantenlänge a, so ergibt sich sofort V = a³. Die Ableitung wäre hier 3*a², was aber nicht der offensichtlich richtigen Formel A = 6*a² entspricht. Deshalb würde ich diese Formel als Spezialfall ansehen und auch so titulieren, damit nicht der Eindruck entsteht, dass diese Vorgehensweise immer richtig wäre. -- Ikarus (nicht signierter Beitrag von 84.59.29.128 (Diskussion) 16:21, 31. Jul 2011 (CEST))

Die Analogie wäre nur mit Ableitung nach der halben Kantenlänge $r:=a/2$ richtig. Dann wäre wie erwartet $V=a^{3}=(2r)^{3}$ und $\operatorname {d} V/\operatorname {d} r=8\cdot 3r^{2}=6\cdot (2r)^{2}=6\cdot a^{2}$. --Daniel5Ko 18:41, 1. Aug. 2011 (CEST)

Oberfläche aus dem Umfang errechnen, das ist für Überschlagsrechnungen nämlich viel einfacher, Umfang mal Umfang geteilt durch pi.

Wieso umfallen?

Die Kugel ist das einzige Objekt im Universum und allen Parallel-Universen, welches tatsächlich !NICHT! umfallen kann punkt. Das mag ja stimmen, aber

• hat meiner Meinung nach nichts mit dem mathematischen Begriff Kugel zu tun.
• Aussagen über Parallel-Universen sollte man vielleicht auch vermeiden, da es sich dabei bereits um theoretische Modelle handelt.
• der Wahrheitswert des Satzes hängt stark von der Definition von umfallen und auch Objekt ab. Würde ich beispielsweise eine Kugel nehmen, deren Schwerpunkt nicht in der Mitte liegt und ihr eine Orientierung (also ein oben zuordnen), könnte diese Kugel nach meiner Meinung durchaus umkippen. Dennoch wäre es immer noch eine Kugel.
• sollte man meiner Meinung nach nicht punkt hinter einen Satz schreiben, weder in einer Diskussion, erst Recht nicht in einem Artikel, auch die Hervorhebung von nicht durch Großschreibung und Ausrufungszeichen sieht m.E. seltsam aus.

Vor allem wegen des ersten Punkts bin ich für die ersatzlose Streichung des Satzes. --Matzedi 10:53, 15. Apr 2006 (CEST)

Euklidische Geometrie?

Gilt der Satz: Die Kugel hat die kleinste Oberfläche von allen Körpern mit einem vorgegebenen Volumen. Von allen Flächen mit vorgegebenen Flächeninhalt umschließt sie das größte Volumen. allgemein oder nur in der euklidischen Geometrie? Gibt es in nichteuklidischen Geometrien Kugeln? --Hutschi 10:42, 5. Mai 2006 (CEST)

ich meine mich zu erinnern, dass euklidische Geometrie der ebenen Geometrie entspricht, ein 3D-Körper wie die Kugel also garnicht in der euklidischen vorkommt. Irre ich mich da? --217.84.43.216 12:56, 14. Jul 2006 (CEST)

Du irrst Dich leider. Die im Artikel beschriebene Kugel (= Vollkugel) ist die der dreidimensionalen Euklidischen Geometrie. Es gibt natürlich auch in anderen Geometrien Kugeln. Z.B. ist in der sphärischen Geometrie eine Kugel vom Radius r um den Mittelpunkt p (p liegt auf der Sphäre) die Menge aller Punkte der Sphäre, welche sphärischen Abstand <= r zu p haben. Offenbar braucht man nicht mal eine glatte Mannigfaltigkeit, um Kugeln zu definieren. Es genügt schon ein metrischer Raum.

Illustration

Kugelkoordinaten

Ich war so frei, die alte, sehr kleine und ziemlich pixelige Illustration durch ein gerendertes Bild zu ersetzen (u.a. auch im Hinblick auf die Druckausgaben) - da ich kein Vollblutmathematiker bin, könnte mir jemand von den Kundigeren sagen, ob die so in Ordnung ist? --DemonDeLuxe :O) 10:14, 14. Jul 2006 (CEST)

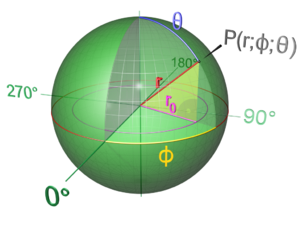
Vielen Dank für die Nachfrage. 1) Φ sieht aus wie das Zeichen für die leere Menge. 2) Φ ist in der Zeichnung nicht recht zu erkennen, auch deshalb erschwert, weil er mit dem 90° Winkel zusammenfällt. 3) Die Bedeutung von r₀ erschloss sich mir auch aus der alten Zeichnung nicht. Anton

Hehe, prima, Du hast prompt den "wunden Punkt" erwischt - ich habe nämlich den ganzen Artikel durchsucht auf der Suche nach Φ (es wurde mir erst durch das Nachsehen hier im Quelltext Deines Beitrags klar, dass das Phi sein soll!)... jetzt hilf mir bitte noch auf die Sprünge, WAS GENAU Phi bezeichnet, dann korrigier' ich das fix. Den Rest habe ich, wie Du siehst, einfach aus der ursprünglichen Zeichnung übernommen - meine eigenen Kenntnisse der Kugel enden leider irgendwo bei 4/3 Pi * r ^3 *g*

Ach so, Zusatzfrage: In der Vorlage sind die griechischen Zeichen groß; in entsprechenden WP-Artikel ist aber stets die Rede von Kleinbuchstaben - was ist denn nun richtig? --DemonDeLuxe :O) 12:22, 14. Jul 2006 (CEST)

Nachtrag: WP bildet - Phi bezeichnet also den Innenwinkel, ja? Hoffe, das passt jetzt alles so - falls nicht, bitte Bescheid geben. --DemonDeLuxe :O) 13:10, 14. Jul 2006 (CEST)

Öfter begegnen mir Winkelbezeichnungen mit Kleinbuchstaben. Großbuchstaben sind gebäuchlicher für Raumwinkel, die hier aber nicht gemeint sind. φ ist der Azimutwinkel. Auf der Erde entspricht ihm der Längengrad. θ ist der Polarwinkel. Ihm entspricht auf der Erde bis die Lage des Nullpunktes der Breitengrad (= Höhenwinkel). Der Artikel sollte die Bezeichnungen des Bildes erklären. Vielleicht erwarten die Autoren, dass man bei Kugelkoordinaten nachschaut? Anton

So, wie ich das jetzt gesehen habe, werden in Formeln Kleinbuchstaben verwendet, während man in den Illustrationen, also am Objekt, öfter die Großbuchstaben sieht. Wie dem auch sei - stimmen denn die Beschriftungen jetzt? Lass mich ned dumm sterben... --DemonDeLuxe :O) 19:58, 14. Jul 2006 (CEST)

Hallo DemonDeLuxe: Vergleiche doch die alte und neue Zeichnung noch einmal miteinander. Ich glaube in der neuen sind jetzt einige gravierende Fehler reingerutscht. Der Punkt P auf der Kugeloberfläche kann doch irgendwo liegen. Bei dir liegt er jetzt genau im 90° Winkel. Auch sollten die Winkel und die Strecke ro an der richtigen stelle stehen. -- Petflo2000 22:19, 14. Jul 2006 (CEST)

Das Kooridnatenkreuz kann ich natürlich noch verschieben, wobei ich allerdings nicht wüsste, wieso die Darstelleung andeuten würde, P sei auf 90° fixiert. Mit dem Winkel, nehme ich an, meinst Du Phi, nach dem ich ja so verzweifelt gefragt hatte - jo, ich sehe, was Du meinst, ändere ich direkt (habe ich erst nach x-tem Studium des Originals als ein bisschen dunklere Linie erkannt). Aber Theta ist korrekt und r0 ebenfalls, laut Vorgabe jedenfalls. r0 ist in der Vorlage blau hervorgehoben. --DemonDeLuxe :O) 06:43, 15. Jul 2006 (CEST)

Ja , so habe ich das gemeint, sehr gut. Aber vielleicht sollte man noch den Text ro etwas nach links (unter oder über die magantafarbene Strecke, dazu gehört ro nämlich). Und irgendwie ist dir beim Ändern der 180° Winkel abhanden gekommen. Aber sonst OK. -- Petflo2000 10:38, 15. Jul 2006 (CEST)

*uffz* na, immerhin... jetzt bekomme ich langsam ein Gefühl für die Nöte des Illustrators, der von dem zu Illustrierenden so eigentlich gar nichts weiß (ich hab' mich um Trigonometrie immer herumgedrückt). Der 180°-Winkel war schon noch da, aber aufgrund der Perspektive halt sehr weit hinten... erschließt sich aber auch aus den anderen dreien, man muss Wikipedia-Leser ja nicht für total doof halten. Trotzdem hab' ich die Achse jetzt 'mal (perspektivisch unkorrekt) entsprechend verlängert und auch wunschgemäß r0 verschoben ("unter" wär' schlecht, weil dann die Farbe durch die Querschnittscheibe verfälscht würde, daher "über"). Merci für die fachkundige Hilfe ;O) --DemonDeLuxe :O) 11:21, 15. Jul 2006 (CEST)

Ich hab da jetzt nichts mehr zu meckern. Tja, es ist nicht so einfach. Ich kenne das auch. Jedesmal weiß es irgend jemand wieder besser. Das einzige was mir noch aufgefallen ist, dass die Winkelbezeichnungen in den Formeln von der Schreibweise her unterschiedlich ist. Habt ihr weiter oben ja auch schon mal beschrieben. Ich versuche mich da noch mal schlau zu machen, was da üblich ist. Vielleicht sollte man das dann noch vereinheitlichen. -- Petflo2000 12:44, 15. Jul 2006 (CEST)

Hurra :O) Und bzgl. der Schreibweise der griechischen Buchstaben - das ist CONTENT, damit habe ich NICHTS zu tun *g* (falls sich da etwas ergeben sollte, das in der Illustration reflektiert werden muss, einfach kurz Bescheid geben, bitte). --DemonDeLuxe :O) 14:00, 15. Jul 2006 (CEST)

Ich hätte da noch etwas zu meckern: Wieso geht der "aufgeschnittene" Teil der Kugel nach links über die 0° hinaus?--Gunther 14:18, 15. Jul 2006 (CEST)

Das ging er ursprünglich nicht - der (willkürlich rechtwinklige) Ausschnitt ging exakt von 0° bis 90°, was ich als "natürlich" ansah, aber nachdem dann oben die Anmerkung kam, das sähe so aus, als ob P zwingend auf der 90 liegen müsse (warum auch immer), habe ich anschließend das Koordinatenkreuz etwas herausgedreht. "Wie man's macht..." ;O) --DemonDeLuxe :O) 14:23, 15. Jul 2006 (CEST)

Der linke Eckpunkt des Ausschnittes ist halt bedeutungslos, sinnvoller wäre es, wenn das der 0°-Punkt wäre.--Gunther 14:44, 15. Jul 2006 (CEST)

Jo, stimmt, der Ausschnitt an sich ist auch bedeutungslos und rein grafisches Element - aber wenn Du das für besser hältst, kann ich dessen Winkel ja zuspitzen und ihn bei 0° beginnen lassen. Ich beuge mich ja der schieren mathematischen Gewalt ;O) --DemonDeLuxe :O) 14:49, 15. Jul 2006 (CEST)

Sonst hat halt jeder der Punkte irgendeine Bedeutung, und da erwarte zumindest ich, dass das auch auf diesen zutrifft. Aber auf jeden Fall vielen Dank, dass Du Dir die ganze Mühe machst.--Gunther 14:57, 15. Jul 2006 (CEST)

Hast ja Recht, "form follows function", ich änder's gleich. Und bzgl. Dank, das ist zwar nett von Dir, aber wir versuchen doch alle, unser Scherflein beuzutragen? Und die guten Artikel sind alle schon geschrieben (<= faule Ausrede). Als altem Pixelschubser sind mir Grafiken wie aus den Urzeiten von MS Paint halt ein Graus, auch wenn die Alternative nur Eyecandy ist. --DemonDeLuxe :O) 15:03, 15. Jul 2006 (CEST)

Die Illustration "Kugelkoordinaten" ist ja wirklich schön, Respekt! Nur leider hat die Abbildung der Kugel eine ernsthafte Schwäche – die sie aber (leider) mit den meisten entsprechenden Abbildungen teilt, wie auch das Suchen nach Kugel-Bildern im Internet zeigt. Um zu verstehen, was falsch ist, schaut mal, wie es richtig wäre, z. B.: [1] ... wenn man nämlich den Äquator als Ellipse sieht, muss der Nordpol direkt zu sehen sein, unterhalb des oberen Kugelrandes. Umgekehrt: Wenn der Nordpol ganz oben am oberen Rand des Kugelbildes ist (wie in dieser Illustration), dann sieht man vom Äquator nur einen Strich (und keine Ellipse). Dieser Fehler ist halt gängig und findet sich an sehr vielen Orten. Kann also passieren ... sollte aber noch geändert werden, finde ich. --Sinuspi (Diskussion) 00:05, 24. Mai 2014 (CEST)

Stimmt ! --Ag2gaeh (Diskussion) 09:21, 24. Mai 2014 (CEST)

Nur bei einer Parallelprojektion, nicht aber bei einer Zentralprojektion, wie sie in der Abbildung verwendet wird. Grüße, --Quartl (Diskussion) 11:33, 24. Mai 2014 (CEST)

In der Vergrößerung sieht man, dass es eine Zentralprojektion ist. Nord- und Südpol sind dann schwach zu erkennen. Die Täuschung wird wohl von der senkrechten grünen Strecke verursacht, die im Bild nach oben und unten gleich weit über den Umriss herausragt. Wenn sie symmetrisch zum Mitelpunkt wäre (was man erwartet), könnte das so nicht sein. Auch die horizontale Strecke "270-90" kann im Original nicht symmetrisch zum Mittelpunkt sein. Aber Sinuspi hat recht, Kugel-Bilder in Büchern sind oft an dieser Stelle nicht korrekt. --Ag2gaeh (Diskussion) 13:30, 24. Mai 2014 (CEST)

Danke – auf die Idee, dass es sich um eine Zentralprojektion handelt, wäre ich allein wohl nie gekommen. Nun kann ich es (ein-)sehen, zumindest an den beiden Ellipsen in der Äquator-Ebene. Wie könnte man das denn vielleicht noch deutlicher machen? Übrigens: Die betr. Abbildung unter Kugelkoordinaten lässt sich wohl nicht mit "Zentralprojektion" begründen, oder? --Sinuspi (Diskussion) 09:03, 25. Mai 2014 (CEST)

Man hätte vielleicht den Längenkreis durch den Kugelpunkt wie den Äquatorkreis ganz projizieren sollen. Dann würde man das Bild des Südpols (hinter der Umrissebene) besser erkennen. Bei der Herstellung des Bildes wurde sicher ein 3D-Programm benutzt, so dass es geometrisch korrekt ist. Die beiden Bilder in Kugelkoordinaten scheinen handgestrickt und wohl nicht korrekt zu sein. Es wäre besser, wenn man (wie in der englischen Version von Kugelkoordinaten) keine Projektionen von Kugel und Kreise einzeichnen würde, was zum Verständnis auch nicht notwendig ist.--Ag2gaeh (Diskussion) 09:43, 25. Mai 2014 (CEST)

Danke, Ag2gaeh – da ich sehe, dass du Fach-Geometer bist: Vielleicht kannst du das dort anregen? --Sinuspi (Diskussion) 11:50, 25. Mai 2014 (CEST)

Ich habe mal das Bild in Kugelkoordinaten ausgetauscht. Ist es so besser ?--Ag2gaeh (Diskussion) 17:06, 25. Mai 2014 (CEST)

Danke – ich find's ausgezeichnet, mein Respekt. Das Dreieck steht klar im (Blick-)Zentrum und da, wo's hingehört, die Kugel ist angemessen bescheiden drumherum, und der Nordpol ist da, wo ich ihn mir wünsche :-). --Sinuspi (Diskussion) 18:58, 25. Mai 2014 (CEST)

Schön, ich würde nur die Formeln aus der Grafik rauslassen (beim Azimutwinkel müsste auch entweder die linke oder die rechte Intervallgrenze rausgenommen werden). Viele Grüße, --Quartl (Diskussion) 19:21, 25. Mai 2014 (CEST)

Formeln sind raus. Grüße ! --Ag2gaeh (Diskussion) 22:17, 25. Mai 2014 (CEST)

Artikel kaputt?

Wenn ich die Seite aufrufe steht da nur: "Vorlage:MediaWiki Noarticletext NS". Bei Version/Autoren wird mir der aber richtig angezeigt...149.201.243.32 00:40, 18. Sep 2006 (CEST)

Geht wieder 19:55, 18. Sep 2006 (CEST)

Herstellung einer Kugel

Und wie baut man nun gezielt eine präzise Kugel? Nur so? -- Kyber 14:03, 8. Feb. 2007 (CET)

Auch die Geschichte der Kugel/Ball-Herstellung und -Anwendung wäre sehr interessant.--Gruß, Helge 23:38, 12. Mai 2008 (CEST)

Verwendung

Die Verwendung von Kugeln (die wichtigsten) gehörten m.E. noch in den Artikel eingepflegt, inkl. geschichtlicher Abriss bzgl. ihrer Nutzung. --Bagerloan 12:23, 26. Mai 2008 (CEST)

Krümmung, Volumen, Oberfläche im R^n

Im Kontext sollte man auch erwähnen, dass die Krümmung der Kugel (2D,3D) stets 1/Radius ist. Außerdem wäre es interessant zu wissen, dass für Volumen (V) und Oberfläche (O) folgendes gilt. $\lim _{n\to \infty }V(1)_{n}=0$ und $\lim _{n\to \infty }O(1)_{n}=0$.--Mordwinzew 00:50, 15. Jun. 2008 (CEST)

---

„Die Kugeloberfläche entspricht übrigens der Mantelfläche eines gleichgroßen Zylinders.“ wie gleich groß? gleichen durchmesser, gleiches volumen? sollte das nicht genauer beschrieben werden? (nicht signierter Beitrag von 213.54.90.92 (Diskussion) ) Jens Liebenau 21:01, 14. Okt. 2008 (CEST)

Die Kugeloberfläche ist z. B. genauso groß wie die Oberfläche eines Zylinders mit $r=r$ und $h=r$!!! (nicht signierter Beitrag von 84.146.236.189 (Diskussion) ) Jens Liebenau 21:01, 14. Okt. 2008 (CEST)

Kugel aus Pyramiden

Die alternative Herleitung ist bisher nicht korrekt. Eine Kugel lässt sich nicht aus endlich vielen Pyramiden zusammensetzen. Man muss vielmehr von unendlich vielen infinitesimalen Pyramiden ausgehen. Wfstb 15:09, 14. Okt. 2008 (CEST)

Jetzt ist sie es aber. Liebe Grüße Jens Liebenau 21:01, 14. Okt. 2008 (CEST)

Volumen, Alternative Herleitung

Ich ersetze "(siehe weiter oben)" durch "(siehe weiter unten)", da es ja um die Herleitung (der Flächenformel) geht, die weiter unten steht. (nicht signierter Beitrag von 80.153.230.14 (Diskussion | Beiträge) 15:40, 13. Feb. 2010 (CET))

Super-Illu

Hallo, vielleicht wäre es mal sinnvoll, geeigente Illustrationen hier einzuflechten, damit auch andere Leute als die Autoren dieser Seite verstehen, um was es geht! Z.B. kann kein Mensch zwischen "Mantelfläche eines Kugelabschnitts" und "Flächeninhalt eines Kugelsegmentes" unterscheiden, zumal die Formeln auch gleich sind! "Außenfläche eines Kugelsegmentes" konnte ich hier auf jeden Fall nicht finden! Liebe Grüße vom Professor 89.58.51.22 21:47, 5. Jan. 2009 (CET)

Kugelring

Wie wär's denn, noch den Kugelring und den dazugehörigen Kugelkappenzylinder mit als Schnittkörper aufzunehmen. Der Kugelring bleibt als Körper über, wenn eine Zylinder-Fläche zentral aus der Kugel das Volumen rausschneidet. Das fantastische am Kugelring ist die Tatsache, das das Volumen nicht von der Größe der Kugel, sondern nur von der Höhe des Kugelrings abhängig ist. (Diese ist natürlich kleiner als der Durchmesser) Das Volumen berechnet sich dann zu V=(Pi/6)*h^3...für h=d ergibt sich dann das ganze Kugelvolumen zu V_K=Pi/6*d^3 Wie gesagt, ein Kugelring der Höhe 1cm hat das Volumen von Pi/6 cm^3, egal ob aus einem Apfel, oder einen Planeten geschnitten. Herleitung kein Problem, da ich anonym schreibe hinterlase ich meine e-mail: etlef.trensinger@rkaehne.de -- 88.79.124.93 10:31, 28. Mai 2009 (CEST)

Eigenschaften

"Nach dem Banach-Tarski-Paradoxon kann eine Kugel in endlich viele Teile zerlegt werden, aus denen sich zwei Kugeln von der Größe des Originals zusammensetzen lassen."

Dieser Satz ist so falsch. Nach Banach-Tarski-Paradoxon würde dieser Satz mehr oder weniger richtig sein, wenn es um eine (mindestens abzählbar) unendliche Zerlegung ginge.

Es ist allerdings so, dass das Paradoxon versucht darzustellen, dass ein bestimmte Volumensbegriff, der auf Puntmengen basiert wiedersprücklich ist, die Kugelzerlegung ist höchstens eine Veranschaulichung des Sachverhalts und hat mit dem mathematischen Begriff der Kugel nichts zu tun. Insbesondere ist dies keine besondere Eigenschaft einer Kugel sondern eine Eigenschaft von geometrischen Objekten an sich und auch nur unter der Voraussetzung eines bestimmten (wiedersprüchlichen) Volumenbegriffs.

Daher bin ich der Meinung, das diese Information auf der Seite nichts zu suchen hat. Nicht in einer korrigierten Version und erst recht nicht in dieser schlicht falschen Version. Daher habe ich den entsprechenden Satz gelöscht.

-- Kaffeejunkie1988 18:52, 4. Aug. 2010 (CEST)

Hallo! Danke für die Erläuterung. Ich werde jetzt deine Änderung nicht mehr zurücksetzen, unter Umständen kann sich aber hier zu deinem Beitrag eine weitere Diskusion entwickeln. Weiterhin viel Spaß hier und Danke für deine Beiträge. Gruß Martin Bahmann 18:54, 4. Aug. 2010 (CEST)

Nach Banach-Tarski gibt es eine derartige Zerlegung der Kugel in 6 Teile (die natürlich allesamt nicht-messbare Punktmengen sind). Ich bin daher dafür, die Löschung rückgängig zu machen, weil die Begründung, die Aussage sei falsch, nicht zutrifft. --Tolentino 10:43, 5. Aug. 2010 (CEST)

Wenn dem so ist, war mir das nicht bewusst, allerdings ist der Hauptgrund für die Löschung immernoch, das diese Information einfach völlig irrelevant für einen Artikel ist, der sich mit der Kugel befasst und dort nichts zu suchen hat. Ich meine man würde ja auch nicht schreiben, dass es eine besondere Eigenschaft der Kugel ist, dass sich ihr Radius mit der Euklidischen Metrik messen lässt, wenn man im euklidischen R^3 ist. Die Kugel ist einfach nur ein mehr oder weniger zufälliges Beispiel für das Paradoxon. -- Kaffeejunkie1988 15:15, 5. Aug. 2010 (CEST)

Zumindest ist aber die Kugel die klassische Formulierung des Paradoxons und nicht nur ein zufällig gewählter Spezialfall einer Verallgemeinerung, die vermutlich weder Banach noch Tarski kannten. --Tolentino 10:44, 6. Aug. 2010 (CEST)

Aber man kann doch nicht ernsthaft behaupten, dass dies eine Eigenschaft ist, die die Kugel als solche auszeichnet. Die Information ist meiner Meinung nach einfach zu sehr aus dem Kontext gerissen. Durch solche Passagen wird eine Art von Halbwissen gefördert, die dazu führt das Leute durch die Gegend laufen "wusstest du dass man eine Kugel bal ba..." was halt nur in einem bestimmten Zusammenhang wirklich Sinn macht. Kaffeejunkie1988 21:58, 15. Aug. 2010 (CEST)

Fehler in Formel

Meiner Ansicht nach ist in der Tabelle ein logischer Fehler.
Das Volumen der Kugelkalotte sollte mit Vkk statt mit Vks (ich kann leider noch keiner Indizes, bin Neuling) bezeichnet werden, damit es nicht zu einer Namenskollision mit dem Volumen der Kugelschicht kommt (an diesem Artikel arbeite ich gerade). --LaoHai 16:56, 14. Jan. 2011 (CET)

Geändert. -- Digamma 18:34, 14. Jan. 2011 (CET)

Winkel undefiniert

In der Formel für die Kugelschicht sind die Winkel $\alpha$ und $\beta$ in den Integrationsgrenzen undefiniert. Habe selbst zuzeit keine Idee, was sie bedeuten sollen, kümmere mich aber am Wochenende drum.
--LaoHai 00:28, 15. Jan. 2011 (CET)

Sorry, zweimal geklickt :-(
--LaoHai 00:29, 15. Jan. 2011 (CET)

Änderungen in 3.2.1 und 3.2.2

Wir, Daniel und Günter, haben die Abschnitte etwas verändert. Nicht weil sie mathematisch nicht einwandfrei wären, sondern weil es uns so grosse Mühe gekostet hat, den urprünglichen Gedankengang zu begreifen. Deshalb haben wir ihn etwas anders und ausführlicher formuliert. Wir meinen, die mathematischen Wikipedia-Artikel sollten nicht nur für Mathematiker da sein, sondern auch mathematisch Interessierten zugänglich. --Gr5959 17:24, 31. Okt. 2011 (CET)

Massenträgheitsmoment einer Hohlkugel

Hallo zusammen,

hier ist im Artikel ein Massenträgheitsmoment einer Holkugel angegeben! Das müsste jedoch soweit ich das im Kopf habe eine Abhängigkeit vom Innen- wie vom Aussendurchmesser haben. Werde es bei Gelegenheit nachschauen! (nicht signierter Beitrag von 194.39.218.10 (Diskussion) 10:34, 18. Apr. 2012 (CEST))

Gemeint ist vermutlich, dass die Masse auf die Oberfläche konzentriert ist, also dass die Kugelschale unendlich dünn ist. --Digamma (Diskussion) 15:28, 18. Apr. 2012 (CEST)

Volumen in höheren Dimensionen

Im Artikel stand:

Das Volumen steigt bis zur 5. Dimension an, und fällt dann wieder gegen null. Für die Oberflächen ergibt sich ein 
lokales Maximum bei einer  Dimensionalität von 7. Das Verhältnis von Volumen zu Oberfläche beträgt 1/n. 
Kugeln in unendlich vielen Dimensionen haben also ein infinitesimal kleines Volumen und eine infinitesimale Oberfläche, 
während Kugeln in 5 beziehungsweise 7 Dimensionen ein maximales Volumen bzw. Oberfläche haben.

Bemerkung dazu: Das Volumen einer Kugel (ab n=2) ist immer kleiner als das Volumen des umschließenden Würfels und immer größer als das Volumen des eingeschlossenen Würfels. Das kann man sicher sagen und es ist sogar einleuchtend.

Der obige Vergleich vergleicht in perfekter Art und Weise aber Äpfel mit Birnen. Er vergleicht Volumina unterschiedlicher Dimensionalität (z.B. eine Fläche mit einem Volumen oder eine Fläche mit einer Länge). Damit ist das ganze nicht mehr invariant gegenüber Skalenveränderungen. Betrachte ich das ganze bei r=0,5 (d.h. d=1, was nicht abwegig ist, bei der Betrachtung von n-dimensionalen Kubi würde man den Durchmesser=Kantenlänge als Referenz verwenden), liegt das Maximum bei n=1, bei r=2,0 (d=4,0) bei n=24, spätestens bei r~8 (d~16) liegt das Maximum bei Zahlen, die wir uns nicht mehr vorstellen können.

Daß das Maximum bei 7 liegt, ist eine spezielle Lösung für d=2 bzw. r=1. Für leicht andere Zahlen liegt es wo ganz anders. Für Hyperkubi ist die Funktion für d=1 bzw. r=0,5 konstant, für Hypersphären fällt sie konstant ab n=1. (nicht signierter Beitrag von 87.171.29.103 (Diskussion) 14:37, 12. Mai 2012 (CEST))

• tatsächlich haben höherdimensionale Räume immer auch größere Volumina, sofern man eine bestimmte Dimension betrachtet, so hat ein 20-dimensionaler Würfel weit mehr 3-D-Volumen als ein 7- oder 5-dimensionaler Würfel. Die Grafik suggeriert gegenteiliges weil in ihr verschiedenen Dimensionen verglichen werden, das ist so als ob man behaupten würde, ein Kreis sei "größer" als eine Kugel - würde man die 2-dim-Flächen vergleichen käme man aber zum genau gegenteiligen (korrekten) Ergebnis.
• Die Formeln sind nicht ganz richtig, sie gelten nur für geradazahlige n. Will man keine Fallunterscheidung machen, müsste der Term n/2 in Abrundungsklammern gefasst werden. --46.115.51.210 20:21, 23. Jun. 2012 (CEST)

Volumen

Es heisst

Volumen

Das Kugelvolumen ist der Rauminhalt einer Kugel, der durch die Kugeloberfläche begrenzt wird.

Vorschlag

Volumen

Das Kugelvolumen ist der Inhalt des Raumes, der durch die Kugeloberfläche begrenzt wird.

Der Satzteil "Das Kugelvolumen ist der Rauminhalt einer Kugel" klingt etwas redundant/ nach Tautologie. (nicht signierter Beitrag von 62.91.26.166 (Diskussion) 17:22, 16. Okt. 2013 (CEST))

Verwendung von theta

Es werden zwei Versionen von theta: $\theta ,\ \vartheta$ benutzt. Man sollte sich auf eine Version einigen und sie auch bei Kugelkoordinaten verwenden. --Ag2gaeh (Diskussion) 09:11, 26. Mai 2014 (CEST)

"Hinweis"

Im Abschnitt über höherdimensionale Verallgemeinerungen findet sich folgender Hinweis: "Hinweis: Diese Begriffe werden nicht einheitlich verwendet. Sphären im Sinne der hier gegebenen Definition werden zuweilen Kugeln genannt. Außerdem sprechen manche Autoren von n‑Sphären, wenn sie (n-1)‑dimensionale Sphären im n-dimensionalen Raum meinen."

Mir sind beide beide Bezeichnungen noch nicht begegnet. Bei der ersten könne ich mir durchaus vorstellen, dass sie außerhalb der Mathematik vorkomm, bei der zweiten eigentlich weniger. Ich wäre deshalb dafür,,zumindest den zweiten Satz des Hinweises herauszunehmen.--Kamsa Hapnida (Diskussion) 14:04, 12. Nov. 2014 (CET)

Hä?

"Das n-dimensionale Volumen einer n-dimensionalen Kugel mit dem Radius r ist"...Unfug.
Ein 3-dimensionales Volumen einer 2-dimensionalen Kugel geht nicht. Einmal "n-dim." kann wohl weg.
Im Übrigen könnten die einfachen Formeln für Volumen (und Oberfläche) auch in die Einleitung, man sucht sich ja blöde.--Mideal (Diskussion) 17:00, 26. Jul. 2016 (CEST)

Eine eindimensionale Kugel ist keine Strecke sondern zwei Punkte

3D Kugel:

$r^{2}=x^{2}+y^{2}+z^{2}$

2D Kreis:

$r^{2}=x^{2}+y^{2}$

1D Zwei Punkte:

$r^{2}=x^{2}$

Die Lösung der letzten Gleichung sind zwei eindimensionale Punkte {-r,r} -- Neoexpert (Diskussion) 00:46, 19. Aug. 2017 (CEST)

Ah, es gibt da ein Missverständnis, mit Kreis oder Kugel kann man auch einen gefüllten Kreis bzw gefüllte Kugel meinen, in dem Fall ist eine eindimensionale Kugel tatsächlich eine Strecke.

-- Neoexpert (Diskussion) 00:53, 19. Aug. 2017 (CEST)

Bild zu Eigenschaften

Das Bild in der engl. Wiki zum Verhältnis der Volumina Zylinder/Kugel finde ich besser. Es zeigt das Wesentliche: Kugel mit umgebenden Zylinder bei beliebigem Kugelradius.--Ag2gaeh (Diskussion) 08:20, 25. Aug. 2017 (CEST)

@Ag2gaeh, danke für deine Hinweise. Die Zeichnung ist jetzt mit einer Kugel mit beliebigem Kugelradius. Bitte habe Verständnis, dass ich die Darstellung so belassen habe, denn ich hatte mich vorher genau an die Beschreibung im Artikel gehalten. Übrigens, du wirst es sicher auch bemerkt haben, im Bild der engl. Wiki dürften die Ellipsen nicht eingezeichnet sein, denn so ist der Zylinder geneigt dargestellt und dies bedarf einer Darstellung mit verkürzter Höhe. --Petrus3743 (Diskussion) 09:47, 25. Aug. 2017 (CEST)

@Petrus3743: Wenn Du die Kugel noch in die Mitte des Zylinders verschiebst, ist das Bild OK. Nur dann erkennt man, dass der Zylinder der Kugel umbeschrieben ist. Die Bemerkung (unter dem Bild) geneigter Zylinder ... solltest Du weglassen. Sie hat mit dem eigentlichen Problem nichts zu tun und verwirrt nur. Das Bild hat nur die Funktion, die räumliche Situation zu verdeutlichen und nicht, um wahre Längen abzulesen. Auch der Text zu dem Volumen-Problem sollte verbessert werden. Z.B.: Das Verhältnis des Volumens einer Kugel (Radius r) zum Volumen des umbeschriebenem Zylinders (Radius r, Höhe 2r, siehe Bild) ist 2/3.--Ag2gaeh (Diskussion) 13:23, 25. Aug. 2017 (CEST)

Danke, der Vorschlag ist eingearbeitet. erledigtErledigt--Petrus3743 (Diskussion) 23:02, 25. Aug. 2017 (CEST)

Noch ein kleiner Schönheitsfehler: Nord- und Südpol (Berührpunkte mit Zylinderdeckel/-boden) der Kugel sollten in dieser Ansicht nicht auf dem Umriss liegen.--Ag2gaeh (Diskussion) 11:29, 26. Aug. 2017 (CEST)

Danke für den Hinweis, ich habe den Zylinder noch etwas neigen müssen um die Trennung der Pole von den Mitten der Ellipsen zu bekommen. Ich hoffe du hast das gemeint...--Petrus3743 (Diskussion) 16:01, 26. Aug. 2017 (CEST)

Um wieviel Grad hast Du den Zylinder gekippt ?--Ag2gaeh (Diskussion) 21:26, 26. Aug. 2017 (CEST)

Pardon, da stimmt was nicht. Ich werde baldmöglichst die Konstruktion genau überprüfen und korrigieren. --Petrus3743 (Diskussion) 22:36, 26. Aug. 2017 (CEST)

Fehler ist behoben, die Projektion war nicht richtig. Der Kippwinkel des Zylinders ist jetzt ca. 20°.--Petrus3743 (Diskussion) 00:44, 27. Aug. 2017 (CEST)

KIammer fehlt

In der Gleichung, welche nach "Durch Einsetzen in die Formel für Drehkörper um die x-Achse erhält man " folgt fehlt die Klammer. (nicht signierter Beitrag von 91.97.101.175 (Diskussion) 09:35, 19. Mai 2018 (CEST))

Erledigt. --Digamma (Diskussion) 10:16, 19. Mai 2018 (CEST)

Oberfläche

Im Beitrag steht: Die Oberfläche ist ${\displaystyle {A}\,={4}\pi {r^{2}}}$.

Es muss - aus meiner Sicht - heißten: Der Oberflächeninhalt $A$ ist ${\displaystyle {A}\,={4}\pi {r^{2}}}$. (nicht signierter Beitrag von 132.187.207.160 (Diskussion) 11:23, 18. Apr. 2019 (CEST))

Habe es verbessert. --Digamma (Diskussion) 11:31, 18. Apr. 2019 (CEST)

Formeln für Nichtmathematiker

Könnte man nicht die Formeln mit aufnehmen, bei denen man sozusagen "zerstörungsfrei" aus dem Umfang einer Kugel die Oberfläche und das Volumen berechnen kann? (nicht signierter Beitrag von 2003:D2:7F3C:D21F:159E:88A5:3541:AE0 (Diskussion) 23:42, 29. Jan. 2021 (CET))

Weil man Nichtmathematikern nicht zumuten/zutrauen kann, den Umfang zunächst durch $2\pi$ zu dividieren, um den Radius zu erhalten? --Digamma (Diskussion) 16:53, 30. Jan. 2021 (CET)