Diskussion:Torus
| Auf dieser Seite werden Abschnitte ab Überschriftebene 2 automatisch archiviert, die seit 30 Tagen mit dem Baustein {{Erledigt|1=--~~~~}} versehen sind. |
Rotationstorus
Ich denke, man sollte den Abschnitt "Eingebettete Tori" auf Rotationstorus verschieben. In seiner jetzigen Form vermittelt der Artikel den falschen Eindruck, dass alle Tori Rotationskörper sein müssen.--Café Bene (Diskussion) 17:54, 4. Mai 2014 (CEST)
Hypertorus
Durch die Umbauarbeiten der letzten Tage führt offenkundig die Weiterleitung Hypertorus ins Nirvana. Es wäre nett, wenn ihr an geeigneter Stelle ein paar Worte zum Hypertorus fallen lassen könntet. Gruß Kein Einstein (Diskussion) 13:33, 25. Mai 2014 (CEST)
Literaturrecherche
Versuch einer Versachlichung der Diskussion: als Maßstab sollte wohl die Verwendung eines Begriffs in der Literatur dienen und wenn es wie oben dargestellt unterschiedliche Verwendungen selbst in der Lehrbuchliteratur gibt hilft nur noch Zählen und ggf. Gewichten nach der Verbreitung von Lehrbüchern. Die verbreitetste Lehrbuchreihe zur Mathematik sind sicherlich die "Graduate Texts in Mathematics", die dort erscheinenden Lehrbücher gelten als Klassiker und stehen in allen Uni-Bibliotheken. Ich habe mir jetzt mal die Mühe gemacht, zu den in meiner Bibliothek stehenden Büchern der Graduate Texts in Mathematics-Reihe nachzuschauen, welche Definition von Torus sie verwenden. (Ich habe alle angeschaut, bei denen man aufgrund des Themas annehmen könnte, dass der Torus im Literaturverzeichnis vorkommt. Es ist natürlich möglich und vielleicht sogar wahrscheinlich, dass ich dabei etwas übersehen habe. Das Ergebnis ist aber so eindeutig, dass es darauf vielleicht nicht mehr ankommt.) Mir ist natürlich auch klar, dass es durchaus Bücher zur elementaren Differentialgeometrie von Kurven und Flächen gibt, wo der Torus als Rotationstorus definiert wird, und dass das auch in Ingenieurwissenschaften so gehandhabt wird. (Wobei, was ich jetzt auf die Schnelle gegoogelt habe, der Torus dort in der Lehrbuchliteratur eher mal als Ubungsaufgabe denn als Teil des Lehrbuchtextes vorkommt.) Jedenfalls in den "Graduate Texts of Mathematics" sieht das Ergebnis so aus:
Lehrbücher, in denen die allgemeine Definition des Torus oder eine Variante davon vorkommt:
Grafakos: Classical Fourier Analysis
Bremaud: Fourier Analysis and stochastic processes
Broecker-tom Dieck: Representations of compact Lie groups
Varadarajan: Lie groups, Lie algebras and their representations
Sepanski: Compact Lie groups
Duistermaat-Kolk: Lie groups
Bump: Lie groups
Warner: Foundations of differentiable manifolds and Lie groups
Olver: Applications of Lie groups to differential equations
Arnold: Mathematical methods of classical mechanics
Farkas-Kra: Riemann surfaces
Forster: Lectures on Riemann surfaces
Berenstein-Gay: Complex variables
Fritzsche-Grauert: From holomorphic functions to complex variables
Borel: Linear algebraic groups
Koblitz: Introduction to elliptic curves and modular forms
Silverman: Arithmetic of elliptic curves
Fulton: Algebraic topology
Rotman: An introduction to algebraic topology
Massey: A basic course in algebraic topology
Vick: Homology theory
Bott-Tu: Differential forms in algebraic topology
Bredon: Topology and geometry
Stillwell: Classical topology and combinatorial group theory
Lee: Introduction to smooth manifolds
Gruenbaum: Convex polytopes
Matousek: Lectures on discrete geometry
Dubrovin-Novikov-Fomenko: Modern geometry
Petersen: Riemannian geometry
Berger-Gostiaux: Differential geometry: manifolds, curves and surfaces
Lehrbücher, in denen der Torus nur als Rotationstorus definiert wird:
keines
--Pugo (Diskussion) 20:58, 8. Jun. 2016 (CEST)
- Wieso schreibst du dann „keines“? Sind Lehrbücher zur elementaren Differentialgeometrie oder Ingenieurwissenschaften denn keine Lehrbücher? Das verstehe ich nicht. In der obigen Diskussion inklusive Verlinkungen sind doch schon zahlreiche Definitionen genannt. Hast du diese Beiträge denn gar nicht gelesen? Zum Beispiel im Beitrag von Ag2gaeh, 12:56, 25. Mai 2016 oder heute(!) von mir das Lehrbuch von Georg Glaeser. Außerdem sind deine Beispiele alle englischsprachig, es geht aber doch hier um die übliche Verwendung der Bezeichnung „Torus“ im deutschen Sprachgebrauch. Verwirrte Grüße -- HilberTraum (d, m) 21:41, 8. Jun. 2016 (CEST)
- Wie gesagt, ich habe nur die Lehrbücher aus der "Graduate Texts in Mathematics"-Reihe durchgeschaut. Natürlich gibt es noch andere Lehrbuchreihen, das hatte ich doch aber vorab auch gesagt. Ich wollte halt einen vollständigen Überblick über eine einzelne Lehrbuchreihe, damit man einenVergleich hat und nicht einfach nur willkürlich ausgewählte Einzelbeispiele als Argument ins Feld geführt werden. Es gibt natürlich noch andere Lehrbuchreihen, z.B. "universitext" oder auch deutsche Lehrbücher und vielleicht wird das Ergebnis dort nicht ganz so extrem ausfallen. Aber jedenfalls belegt die obige Liste doch, dass die im Artikel verwendete allgemeine Torus-Definition nicht auf ein einzelnes Gebiet der Mathematik beschränkt ist, sondern sich in Lehrbüchern aus allen Gebieten findet, auch in eher anwendungs-orientierten.--Pugo (Diskussion) 21:59, 8. Jun. 2016 (CEST)
Es dreht sich doch nicht um die Verbreitung der Definition im geometrischen/topologischen Sinn, sondern die Benennung im Fall der Fläche. Entsprechend müsste man hier deutschsprachige Lehrbücher der (elementaren) Geometrie/Differentialgeometrie durchgehen um einen Vergleich zu haben. Im älteren, aber klassischen Lehrbuch von Coxeter (Unvergängliche Geometrie) heisst es nur Torus (gemeint ist da meist der Rotationstorus). Im neueren Buch von Agricola, Friedrich, Elementargeometrie ist explizit von Rotationstorus die Rede, ebenso im englischen Audin Geometry, 2002, (Torus of revolution), genauso häufig findet man aber auch neuere Bücher, in denen einfach Torus geschrieben wird (für die Fläche), zum Beispiel Bär, Elementare Differentialgeometrie, De Gruyter 2010, S. 185. Wie sieht es denn mit Schulbüchern aus ? --Claude J (Diskussion) 07:47, 9. Jun. 2016 (CEST)
- Ich bezweifle, dass der Torus in Schulbüchern vorkommt, lasse mich aber natürlich gerne eines besseren belehren.
- Die oben aufgeführten Uni-Lehrbücher sind jedenfalls nicht nur aus Geometrie und Topologie, sondern auch aus Gebieten wie Fourier-Analysis, Differentialgleichungen, Funktionentheorie und Elliptische Kurven.
- Und, wie schon mehrfach gesagt, wir (ich) haben den Artikel ja inzwischen so umgeschrieben, dass die rotationssymmetrische Variante im Artikeltext und auch in der Einleitung am Anfang steht, und dort auch die für Ingenieure relevanten Koordinaten vorkommen. Die speziellen Formeln zum Außenvolumen eines Spindeltorus, Tragheitsmoment eines Volltorus etc. sind aber mMn im Spezialartikel Rotationstorus besser aufgehoben (bzw. sollten in weitere Spezialartikel wie Spindeltorus ausgelagert werden) und müssen nicht im Artikel Torus, der ja eher ein Uberblicksartikel zu verschiedenen Arten von Tori ist, erscheinen.--Pugo (Diskussion) 08:10, 9. Jun. 2016 (CEST)
Beispiele von deutscher Literatur über den TORUS als Fläche:
- Bronstein & Semendjajew: Taschenbuch der Mathematik, Harri Deutsch Verlag (1983), ISBN 3871444928, S. 253.
- R. Courant: Vorlesungen über Differential- und Integralrechnung 2, Springer-Verlag, 1963, S. 145, 244.
- A. Hoffmann & B. Marx & W. Vogt: Mathematik für Ingenieure 2, Pearson Studium (2006), ISBN 978-3-8273-7114-0, S. 83.
- K. Meyberg & P. Vachenauer: Höhere Mathematik 1, Springer Lehrbuch (1995), ISBN 3-540-59188-5, S. 205, 471.
- Kleine Enzyklopädie Mathematik, Verlag Harri Deutsch (1977), ISBN 3871443239, S. 218.
- Ulrich Graf, Martin Barner: Darstellende Geometrie. Quelle & Meyer, Heidelberg 1961, ISBN 3-494-00488-9, S.202,209.
- C. Leopold: Geometrische Grundlagen der Architekturdarstellung. Verlag W. Kohlhammer, Stuttgart 2005, ISBN 3-17-018489-X, S.123,129.
- Georg Glaeser: Geometrie und ihre Anwendungen in Kunst, Natur und Technik, Springer-Verlag,(2014),ISBN 9783642418525, S. 216.
--Ag2gaeh (Diskussion) 10:34, 9. Jun. 2016 (CEST)
- Wie gesagt, ich hatte einen vollständigen Überblick über eine einzelne Lehrbuchreihe versucht, damit man einen Vergleich hat und nicht einfach nur willkürlich ausgewählte Einzelbeispiele als Argument ins Feld geführt werden. Das von mir gewählte Beispiel "Graduate Texts of Mathematics" mag insofern untypisch sein, dass die Reihe sich explizit an "graduate students" ausschließlich in Mathematik richtet. Die Bezeichnung des Rotationstorus als Torus kommt in der Lehrbuchliteratur zweifellos vor, aber sie ist jedenfalls nicht die überwiegende oder gar ausschließliche Verwendung des Wortes "Torus".--Pugo (Diskussion) 15:50, 9. Jun. 2016 (CEST)
- Ag2gaeh: Als Ergänzung zu meinem letzten Beitrag auf Portal Diskussion:Mathematik: Ich habe gerade das Buch Marcel Berger, Geometry I (Universitext), Springer Verlag vorliegen. Die Bezeichnung "Torus" kommt dort an verschiedenen Stellen vor, u.a.:
- Abschnitt 1.7.7.4 (S. 22, es geht um "Tilings and crystallographic groups"): "... which has as quotient the two-torus ..."
- 10.12.1: "Let T be a torus, that is, the surface of revolution created when a circle rotates around al line disjoint from and coplanar with it."
- Die benutzte Definition hängt also sehr stark vom Kontext ab. Im Buch "Geometry Revealed: A Jacob's Ladder to Modern Higher Geometry" kommt laut Google-Vorschau an 10 Stellen die Bezeichnung "torus of revolution" vor. --Digamma (Diskussion) 16:36, 9. Jun. 2016 (CEST)
- Ag2gaeh: Als Ergänzung zu meinem letzten Beitrag auf Portal Diskussion:Mathematik: Ich habe gerade das Buch Marcel Berger, Geometry I (Universitext), Springer Verlag vorliegen. Die Bezeichnung "Torus" kommt dort an verschiedenen Stellen vor, u.a.:
Eine Bitte
Kopiert von Portal Diskussion:Mathematik/Archiv/2016/2 durch (nicht signierter Beitrag von 128.176.186.7 (Diskussion) 09:23, 27. Jul. 2017 (CEST))
Nach einer längeren Diskussion besteht der Kollege Pugo weiterhin auf der mit der Geometrie-Literatur nicht kompatiblen Bezeichnung Rotationstorus statt dem üblichen Torus (Geometrie). --Ag2gaeh (Diskussion) 19:56, 8. Jun. 2016 (CEST)
- Mir ist nicht klar, warum du die Bezeichnung "Rotationstorus" für falsch hältst bzw. für "mit der Geometrie-Literatur" nicht kompatibel. --Digamma (Diskussion) 20:18, 8. Jun. 2016 (CEST)
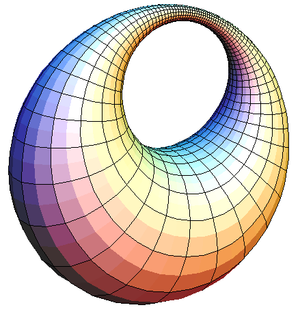
- Ergänzende Frage: Ist das rechts Abgebildete für dich ein Torus? --Digamma (Diskussion) 20:23, 8. Jun. 2016 (CEST)
- Digamma, ich weiß nicht, was du mit dieser Frage bezweckst. Es geht hier doch nicht darum, was wir oder du oder ich unter einem Torus verstehen. Es geht darum, was in der Literatur die üblichste Definition für den Begriff „Torus“ ist. Wenn wir das irgendwann mal endlich herausgefunden haben, können wir sicher locker die Frage beantworten, ob das rechts Abgebildete ein Torus ist oder nicht. (Laut Wikipedia scheint das eine dupinsche Zyklide zu sein … wieder was gelernt ;) -- HilberTraum (d, m) 22:06, 8. Jun. 2016 (CEST)
- Ich habe die Frage so gestellt, weil ich mir gar nicht so klar darüber bin, worüber hier eigentlich gestritten wird. Ag2gaeh scheint eben nicht (nur) die allgemeine Definition eine Torus zu bezweifeln, sonder er bestreitet, dass "Rotationstorus" die richtige Bezeichnung für einen Rotationstorus ist.
- "Es geht darum, was in der Literatur die üblichste Definition für den Begriff „Torus“ ist." M.E. gibt es so etwas in der Mathematik in der Regel nicht. Jeder Autor definiert einen Begriff in der Regel nicht allgemein, sondern nur für sein Buch bzw. das von ihm betrachtete Gebiet. Die Literatur schreibt eben in der Regel keine Enzyklopädien, sondern Lehrbücher, für bestimmte Teilgebiete. Deshalb ist es ganz logisch, dass jemand, der über Riemannsche Geometrie schreibt, den Begriff Torus anders definiert, als jemand, der über Flächen im dreidimensionalen euklidischen Raum schreibt, oder jemand, der über Riemannsche Flächen schreibt. Keiner von denen hat aber in der Regel die Absicht, eine allgemeingültige Definition zu geben. --Digamma (Diskussion) 07:05, 9. Jun. 2016 (CEST)
@Benutzer:Digamma: Nenne mir 5 namhafte nicht-topologische Literaturstellen, wo die Torusfläche als Rotationstorus definiert wird. Nenne mir eine nichttopologische Stelle, wo die Dupinsche Zyklide als Torus definiert wird. Schlage 10 nichttopologische Mathematik-Bücher auf, die die Torusfläche behandeln, und sage mir, findest Du die Torusfläche im Index unter Torus oder Rotationstorus ? Nenne mir eine anderssprachige WIKI-Seite, die die Torusfläche nicht Torus (in der jeweiligen Sprache) nennt. --Ag2gaeh (Diskussion) 08:32, 9. Jun. 2016 (CEST)
- Ag2gaeh, ich glaube, du meinst nicht: "wo die Torusfläche als Rotationstorus definiert wird", sondern "wo die Torusfläche als Roationstorus bezeichnet wird". Anders ausgedrückt: Du möchtest sagen, in nicht-topologischer Literatur ist immer der Rotationstorus gemeint, wenn von "Torus" gesprochen wird. Sehe ich das richtig? Du wirst aber nicht bezweifeln, dass es eben genug (von mir aus "topologische") Literatur gibt, wo mit "Torus" einfach der topologische Typ diesr Fläche gemeint ist (bzw. konkret z.B. oder . Und den Rotationstorus als "Rotationstorus" zu bezeichnen, ist ja wohl nicht falsch (höchstens nach deiner Behauptung unüblich). Nun schreiben wir eben kein Lehrbuch zu einem Thema aus einem bestimmten Gebiet, sondern eine Enzyklopädie. Wie sollen wir deiner Meinung nach deinen engen Begriff des Torus von dem allgemeinen Begriff unterscheiden? Der Zusatz "(Geometrie)" ist m.E. nicht geeignet, weil auch oder Gegenstand der Geometrie sind. "Rotationstorus" ist einfach m.E. eine Bezeichnung, die sehr gut geeignet ist, den speziellen Begriff vom allgemen abzugrenzen und sich auch eigentlich von selbst erklärt. Wer nach "Torus" (in deinem Sinn) sucht und auf "Rotationstorus" verwiesen wird, sollte eigentlich kein Problem haben. --Digamma (Diskussion) 14:17, 9. Jun. 2016 (CEST)
- Ergänzung: es ist keineswegs der Fall, dass in nicht-topologischer Literatur mit "Torus" der Rotationstorus gemeint ist. Von den 30 in Diskussion:Torus#Literaturrecherche aufgelisteten GTM-Bänden sind 23 zu nicht-topologischen Themen, etwa zur Fourier-Analysis (wo der Torus zur Definition der höher-dimensionalen Fourier-Transformation benötigt wird), in der Funktionentheorie (Modulfunktionen sind auf dem Torus definiert) und der Theorie elliptischer Kurven (inkl. Kryptographie), in der Theorie gewöhnlicher Differentialgleichungen und integrabler Systeme (Satz von Liouville: Integrabilität folgt aus der Existenz invarIanter Tori), in der Himmelsmechanik (invarIante Tori in der Stabilitätstheorie), in der diskreten Geometrie, in der Differentialgeometrie etc. pp. Dagegen kommen Rotationstori innerhalb der Mathematik eigentlich nur als didaktisches Konzept in Lehrbüchern zur elementaren Differentialgeometrie vor, selbst in weiterführenden Lehrbüchern zur Differentialgeometrie spielen sie dann keine nennenswerte Rolle mehr.
- Trotzdem ist es sicher sinnvoll, wie es von verschiedenen Autoren angeregt worden war, den Artikel mit dem didaktischen Konzept des Rotationstorus zu beginnen und erst danach die allgemeine Definition zu bringen. Aber das ist ja im Artikel inzwischen auch schon seit einigen Wochen so umgesetzt.--Pugo (Diskussion) 15:25, 9. Jun. 2016 (CEST)
- Es macht vermutlich keinen Sinn, hier und auf Diskussion:Torus über das gleiche zu diskutieren. Deshalb von meiner Seite aus Fortsetzung dort. --Digamma (Diskussion) 16:24, 9. Jun. 2016 (CEST)
Hallo, also ich finde Digamma und Pugo haben in ihrem letzten längeren Statement recht. Ich halte den aktuellen Zustand für in Ordnung, schließlich ist der Rotationstorus ein Spezialfall des allgemeinen (topologischen) Torus. Daher ist es für mich auch okey, wenn er ein Lemma bekommt, das nicht so verbreitet ist. Nachweisbar ist der Name schließlich. Die Differenz hier ließe sich aus meiner Sicht nur damit lösen, dass man die Artikel anders zueinander schneidet. Einen Vorschlag dazu hatte ich auf der Diskussionsseite bereits getan. Dieser fand vermutlich keinen Anklang, daher schlage ich nun noch vor, dass wir den Artikel Rotationstorus wieder in den Artikel Torus integrieren. So ist die ja auch in der englischen Wikipedia. Ich selbst bin dem gegenüber recht leidenschaftslos.--Christian1985 (Disk) 17:33, 9. Jun. 2016 (CEST)
- Nach der Auslagerung von Spindeltorus und Volltorus steht ja in Rotationstorus eigentlich nichts mehr, was nicht (inzwischen) auch im entsprechenden Abschnitt in Torus vorkommt. Willst Du Rotationstorus in eine Weiterleitung umwandeln?--Pugo (Diskussion) 17:51, 9. Jun. 2016 (CEST)
- Ist die Frage an mich gestellt? Im aktuellen Zuständ fände ich eine Weiterleitung besser. --Christian1985 (Disk) 17:39, 10. Jun. 2016 (CEST)
- Ich habe das dann so umgesetzt.
- Archivierung dieses Abschnittes wurde gewünscht von: Pugo (Diskussion) 10:23, 11. Jun. 2016 (CEST)
Ende der Kopie
Benutzer Diskussion:Funkmich008
Kopiert von der Diskussionsseite Benutzer Diskussion:Funkmich008 durch (nicht signierter Beitrag von 128.176.186.7 (Diskussion) 09:25, 27. Jul. 2017 (CEST))
Hallo, Du hast In Torus Formeln zur Volumenberechnung eingefügt. Der Torus ist aber eine 2-dimensionale Fläche und hat deshalb kein Volumen. Die von Dir angegebenen Formeln gehören in den Artikel Volltorus. --S. K. Kwan (Diskussion) 01:34, 28. Feb. 2017 (CET)
- Ich habe Deinen Text jetzt nach Volltorus#Volumen des Volltorus verschoben und dementsprechend in Torus herausgenommen.--S. K. Kwan (Diskussion) 03:06, 28. Feb. 2017 (CET)
Ende der Kopie.
- Das Datum scheint fehlerhaft zu sein. -- Karl Bednarik (Diskussion) 09:43, 27. Jul. 2017 (CEST).
- Das ist eine Kopie von einer anderen Diskussionsseite. Ich habe das inzwischen gekennzeichnet. Was das soll, weiß ich ich auch nicht. --Digamma (Diskussion) 13:13, 27. Jul. 2017 (CEST)
- Ich hatte das rünerkopiert weil ich noch einen längeren Kommentar dazu schreiben wollte- wozu ich aber wohl erst nächste Woche kommen werde, sorry.
- Das Datum scheint fehlerhaft zu sein. -- Karl Bednarik (Diskussion) 09:43, 27. Jul. 2017 (CEST).
Anwendungen
Wir sollten vielleicht diskutieren, welche außermathematischen Anwendungen (oder Erscheinungsformen des Torus in der Natur) wichtig genug sind, um im Artikel erwähnt zu werden. Der Link zur Kernfusionstechnologie würde ja bei einer der letzten Änderungen entfernt (möglicherweise zu Recht, kann ich nicht beurteilen). Sind die in Architektur und darstellender Geometrie vorkommenden Tori relevant genug für einen eigenen Abschnitt? Was ist mit Computerspielen, die den Torus (in Gestalt eines Rechtecks, dessen gegenüberliegende Seiten identifiziert wurden) verwenden? Sind Tori irgendwo in der Technik von Bedeutung? Natürlich sollten nicht alle Anwendungen aufgelistet werden, sondern nur die, die in einschlägigen Lehrbüchern des jeweiligen Fachgebiets eine Rolle spielen.--S. K. Kwan (Diskussion) 09:08, 16. Aug. 2017 (CEST)
- Ein bisschen was zu Computerspielen steht schon im Abschnitt „Konstruktion zweidimensionaler Tori aus einem Quadrat oder Parallelogramm“ (wo man es vielleicht nicht unbedigt erwarten würde). Als leckere Anwendungen würden mir noch Doughnuts, Bagels und Tintenfischringe einfallen, aber das sind ja eher Volltori ;-) -- HilberTraum (d, m) 13:41, 16. Aug. 2017 (CEST)
Torus = Hohlring?
Ich als Laie kann mir, ohne dass es für mich sichtbar ist, nur sehr schwer vorstellen, was ein Torus ist. Wäre ein "Trivialname" wie "Hohlring" oder "hohler Ring" da nicht besser? Zumindest könnte ich gleich (und bestimmt auch andere fachfremde Leute) etwas damit anfangen.
- Er nuss nicht hohl sein, sein Volumen kann gefüllt sein, Vollgummireifen statt Luftreifen-Schlauch... Allerdings heißt der dann hier in WP Volltorus. Mit dieser Nomenklatur haben sich wohl wieder einmal die „reinen“ Mathematiker durchgesetzt. Im praktisch-technischen Sprachgebrauch heißt auch der Volltorus schlicht Torus. -- Trivialnamen selbst zu erfinden und einzuführen ist nicht sinnvoll. WP sollte sich als Nachschlagewerk schon an denjenigen Sprachgebrauch halten, der in der Literatur zu finden ist. Zum Erläutern in der Einleitung könnte man als Beispiel „Oberfläche eines Rettungsrings“ o. ä. nennen. --UvM (Diskussion) 15:39, 4. Jan. 2019 (CET)
So war es auch gemeint, ein Name den jeder auf Anhieb versteht. Den "Torus" als Fachbegriff zu ersetzen, war nicht mein Gedanke. Wie Du so schön noch ergänzt hast, so könnte man es nennen. Oder: "Der Torus entspricht, vereinfacht beschrieben, der Oberfläche und Aussehen eines Rettungs(-rings)." Wäre das was?
- Das steht doch schon ganz ähnlich in der Einleitung (wie ich jetzt erst sehe). Wieso kannst/konntest du dir das so schwer vorstellen? Übrigens ist es netter, wenn man seine Diskussionsbeiträge mit ~~~~ (4 mal Tilde) unterzeichnet. „Mit einem Hauch von virtueller Identität diskutiert es sich leichter“... --UvM (Diskussion) 18:05, 4. Jan. 2019 (CET)
Ja, so ähnlich aber nicht ganz... Weil ich es mit dieser Erklärung eben nur schwer kann.2A02:810D:A480:2295:1020:F0B:C2EE:D629 18:12, 4. Jan. 2019 (CET)
- Würde es helfen, wenn da "Oberfläche eines Rettungsrings" stehen würde? --Digamma (Diskussion) 18:16, 4. Jan. 2019 (CET)
Das Volumen und die Oberfläche des Torus werden hier offenbar nur für den regelmäßigen Rotationskörper dargestellt (siehe Volltorus). Als Nichtmathematiker kann ich das nicht alles nachvollziehen. --Kulturkritik (Diskussion) 18:27, 16. Feb. 2021 (CET)
Figur
LOL :) Was Das??? Also mal paar Werte eingesetzt und es geplottet habe (Wenn Zeit finde Bild hochlade) Torus... sicher nicht. So aussieht wie... Doppelkegel und.. verschoben Doppelkegelinvers... Ich glaube dass Fehler war, dass man Wurzel zieht und dann ... quadriert und häää???? seitwann sowas erlaubt... Also, dass erstmal lösche... vielleicht ja noch überzeugt werde wenn 200 euro geschenkt bekomme z.B :D Weil dann -100=+100 werden und ich schuldenfrei bin :D hihi (genau wie wenn gleichung quadriert und dann wurzel gezogen würde....) --123Frosch123 (Diskussion) 20:04, 5. Jun. 2020 (CEST)
- Was hast du denn eingeworfen ;)? -- HilberTraum (d, m) 20:18, 5. Jun. 2020 (CEST)
Dann bitte Fehler erkläre :( bitte bitte.... ich verstehe nicht, wie das geht... So gemacht habe: Offensichtlich wenn z=0 man Doppelring erhält (wie Torus auch) gut dann Gleichung anders...
umstellen. okay? gut. Dann mal R=5 und r=1 gesetzt. ja? dann also Funktion F(x,y) gebastelt habe. Gut 3D objekt also... jetzt mal Tupel betrachte wo x=0 (und weil symetrie.. gleiche wenn y=0) und jetzt wertetabelle...
| Y = | Z= | |
| 0 | +,- | |
| 9,-9,1,-1 | ,- | |
| 8,-8,2,-2 | ,- | |
| 7,-7,3,-3 | ,- | |
| 6,-6,4,4 | 0 |
und so dann zwei doppelkegel erhalte, innere kreis, normale und äußere, falschrum (leider gerade wenig platz hatte, nochmal zeichnen kann aber was ich meine) (nicht signierter Beitrag von 123Frosch123 (Diskussion | Beiträge) 22:57, 5. Jun. 2020 (CEST))
ja... ups. Vorzeichenfehler... gerade gesehen... es heisst ... wenn man annimmt... tatsächlich was man bekommt: Doppelkegel. und ja alles gut... a=b => a^2=b^2... --123Frosch123 (Diskussion) 05:21, 6. Jun. 2020 (CEST)