Sehnenviereck

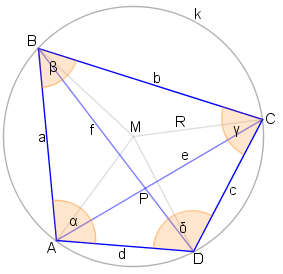
Ein Sehnenviereck ABCD mit Umkreis k

Ein Sehnenviereck ist ein Viereck, dessen Eckpunkte auf einem Kreis liegen, dem Umkreis des Vierecks. Folglich sind alle Seiten des Sehnenvierecks Sehnen des Umkreises. Üblicherweise meint man mit Sehnenviereck ein nicht-überschlagenes Sehnenviereck; es ist notwendigerweise konvex.

Das gleichschenklige Trapez und das Rechteck sind besondere Sehnenvierecke.

Sätze

Für jedes Sehnenviereck gilt der Sehnensatz:

• Die Produkte je zweier gegenüberliegender Diagonalenabschnitte sind gleich groß. Das heißt, wenn $P$ der Schnittpunkt der beiden Diagonalen ${\overline {AC}}$ und ${\overline {BD}}$ ist, so gilt ${\overline {AP}}\cdot {\overline {CP}}={\overline {BP}}\cdot {\overline {DP}}$.

Die folgenden Sätze gelten nur für nicht-überschlagene Sehnenvierecke ABCD:

• Gegenüberliegende Winkel ergänzen sich zu 180°, also $\alpha +\gamma =\beta +\delta =180^{\circ }$.
• Satz von Ptolemäus: Die Summe der Produkte gegenüberliegender Seiten des Sehnenvierecks ist gleich dem Produkt der Diagonalen: ${\overline {AB}}\cdot {\overline {CD}}+{\overline {BC}}\cdot {\overline {DA}}={\overline {AC}}\cdot {\overline {BD}}$.

Eigenschaften

Im Sehnenviereck beträgt die Winkelsumme der gegenüberliegenden Winkel 180°.

$\alpha +\gamma =180^{\circ }$

$\beta +\delta =180^{\circ }$

Der Beweis ergibt sich unmittelbar aus dem Kreiswinkelsatz, da zwei gegenüberliegende Winkel des Sehnenvierecks Umfangswinkel über zwei komplementären Kreisbögen sind, deren Mittelpunktswinkel sich zu 360° ergänzen. Da Umfangswinkel halb so groß sind wie Mittelpunktswinkel über dem gleichen Bogen, müssen sich die Umfangswinkel zu 360°/2 = 180° ergänzen.

Ein anderer Beweis findet sich im Beweisarchiv.

Die Umkehrung dieser Aussage stimmt auch, d. h. ist in einem Viereck die Summe gegenüberliegender Winkel 180°, dann ist es ein Sehnenviereck.

Formeln

Mathematische Formeln zum Sehnenviereck
Flächeninhalt	$A={\sqrt {(s-a)\cdot (s-b)\cdot (s-c)\cdot (s-d)}}$ mit $s={\frac {a+b+c+d}{2}}$
	$A={\frac {e\cdot (a\cdot b+c\cdot d)}{4\cdot R}}={\frac {f\cdot (a\cdot d+b\cdot c)}{4\cdot R}}$
Länge der Diagonalen	$e={\sqrt {\frac {(a\cdot c+b\cdot d)\cdot (a\cdot d+b\cdot c)}{a\cdot b+c\cdot d}}}$
	$f={\sqrt {\frac {(a\cdot b+c\cdot d)\cdot (a\cdot c+b\cdot d)}{a\cdot d+b\cdot c}}}$
Umkreisradius	$R={\frac {1}{4\cdot A}}\cdot {\sqrt {(a\cdot b+c\cdot d)\cdot (a\cdot c+b\cdot d)\cdot (a\cdot d+b\cdot c)}}$
Innenwinkel	$\alpha +\gamma =\beta +\delta =180^{\circ }$

Die zuerst genannte Formel für den Flächeninhalt ist eine Verallgemeinerung des Satz des Heron für Dreiecke und wird auch als Satz von Brahmagupta oder Formel von Brahmagupta bezeichnet. Hierbei fasst man ein Dreieck als ein ausgeartetes Sehnenviereck auf, dessen vierte Seite die Länge 0 besitzt, d. h. zwei seiner Eckpunkte liegen aufeinander. Die Formel von Brahmagupta kann zur Formel von Bretschneider verallgemeinert werden, diese fügt Brahmaguptas Formel einen Korrekturterm, der im Falle eines Sehnenvierecks 0 ist, hinzu und gilt dann für beliebige Vierecke.

Ein Viereck mit festen, geordneten Seitenlängen hat genau dann den größtmöglichen Flächeninhalt, wenn es ein Sehnenviereck ist. Ebenso hat ein Vieleck genau dann den größten Flächeninhalt, wenn es ein Sehnenvieleck ist.

Weitere Formeln

Nach dem Satz des Pythagoras gilt für die Flächeninhalte der Dreiecke ABM, BCM, CDM und DAM

$A(ABM)={\frac {1}{2}}\cdot a\cdot {\sqrt {r^{2}-\left({\frac {a}{2}}\right)^{2}}}={\frac {a}{4}}\cdot {\sqrt {4\cdot r^{2}-a^{2}}}$ und entsprechend

$A(BCM)={\frac {b}{4}}\cdot {\sqrt {4\cdot r^{2}-b^{2}}}$

$A(CDM)={\frac {c}{4}}\cdot {\sqrt {4\cdot r^{2}-c^{2}}}$

$A(CDM)={\frac {d}{4}}\cdot {\sqrt {4\cdot r^{2}-d^{2}}}$

Der Flächeninhalt des Sehnenvierecks ABCD ist die Summe dieser 4 Flächeninhalte, also gilt

${\begin{aligned}A&=A(ABM)+A(BCM)+A(CDM)+A(CDM)\\&={\frac {a}{4}}\cdot {\sqrt {4\cdot r^{2}-a^{2}}}+{\frac {b}{4}}\cdot {\sqrt {4\cdot r^{2}-b^{2}}}+{\frac {c}{4}}\cdot {\sqrt {4\cdot r^{2}-c^{2}}}+{\frac {d}{4}}\cdot {\sqrt {4\cdot r^{2}-d^{2}}}\\&={\frac {1}{4}}\cdot \left(a\cdot {\sqrt {4\cdot r^{2}-a^{2}}}+b\cdot {\sqrt {4\cdot r^{2}-b^{2}}}+c\cdot {\sqrt {4\cdot r^{2}-c^{2}}}+d\cdot {\sqrt {4\cdot r^{2}-d^{2}}}\right)\end{aligned}}$

Bezeichnet man die Mittelpunktswinkel, die den Seiten $a$, $b$, $c$, $d$ gegenüber liegen, mit $\alpha _{m}$, $\beta _{m}$, $\gamma _{m}$, $\delta _{m}$, dann gilt nach der Definition von Sinus und Kosinus

$\sin \left({\frac {\alpha _{m}}{2}}\right)={\frac {a}{2\cdot r}}$ und $\cos \left({\frac {\alpha _{m}}{2}}\right)={\frac {\sqrt {4\cdot r^{2}-a^{2}}}{2\cdot r}}$, also $\sin \left({\frac {\alpha _{m}}{2}}\right)\cdot \cos \left({\frac {\alpha _{m}}{2}}\right)={\frac {a}{2\cdot r}}\cdot {\frac {\sqrt {4\cdot r^{2}-a^{2}}}{2\cdot r}}={\frac {a\cdot {\sqrt {4\cdot r^{2}-a^{2}}}}{4\cdot r^{2}}}$. Aus der Formel für die Doppelwinkelfunktionen folgt

$a\cdot {\sqrt {4\cdot r^{2}-a^{2}}}=4\cdot r^{2}\cdot \sin \left({\frac {\alpha _{m}}{2}}\right)\cdot \cos \left({\frac {\alpha _{m}}{2}}\right)=2\cdot r^{2}\cdot \sin(\alpha _{m})$ und entsprechend

$b\cdot {\sqrt {4\cdot r^{2}-b^{2}}}=2\cdot r^{2}\cdot \sin(\beta _{m})$

$c\cdot {\sqrt {4\cdot r^{2}-c^{2}}}=2\cdot r^{2}\cdot \sin(\gamma _{m})$

$d\cdot {\sqrt {4\cdot r^{2}-d^{2}}}=2\cdot r^{2}\cdot \sin(\delta _{m})$

Einsetzen in die Formel für den Flächeninhalt ergibt

${\begin{aligned}A&={\frac {1}{4}}\cdot \left(2\cdot r^{2}\cdot \sin(\alpha _{m})+2\cdot r^{2}\cdot \sin(\beta _{m})+2\cdot r^{2}\cdot \sin(\gamma _{m})+2\cdot r^{2}\cdot \sin(\delta _{m})\right)\\&={\frac {r^{2}}{2}}\cdot \left(\sin(\alpha _{m})+\sin(\beta _{m})+\sin(\gamma _{m})+\sin(\delta _{m})\right)\end{aligned}}$

Gleichungen

Für die Innenwinkel eines Sehnenvierecks gelten folgende Gleichungen:

$\sin(\alpha )={\frac {2\cdot {\sqrt {(s-a)\cdot (s-b)\cdot (s-c)\cdot (s-d)}}}{a\cdot d+b\cdot c}}$

$\cos(\alpha )={\frac {a^{2}+d^{2}-b^{2}-c^{2}}{2\cdot (a\cdot d+b\cdot c)}}$

$\tan \left({\frac {\alpha }{2}}\right)={\sqrt {\frac {(s-a)\cdot (s-d)}{(s-b)\cdot (s-c)}}}$

Für den Schnittwinkel der Diagonalen gilt:

$\tan \left({\frac {\theta }{2}}\right)={\sqrt {\frac {(s-b)\cdot (s-d)}{(s-a)\cdot (s-c)}}}$

Für den Schnittwinkel der Seiten a und c gilt:

$\cos \left({\frac {\varphi }{2}}\right)={\sqrt {\frac {(s-b)\cdot (s-d)\cdot (b+d)^{2}}{(a\cdot b+c\cdot d)\cdot (a\cdot d+b\cdot c)}}}$

Siehe auch

• Japanischer Satz für Sehnenvierecke
• Tangentenviereck
• Sehnenvieleck

Literatur

• H. Fenkner, K. Holzmüller: Mathematisches Unterrichtswerk. Nach den Richtlinien für die Lehrpläne der höheren Schulen Preußens neu bearbeitet von Dr. Karl Holzmüller. Geometrie. Ausgabe A in 2 Teilen. 12. Auflage. I. Teil. Verlag von Otto Salle, Berlin 1926. 
• Theophil Lambacher, Wilhelm Schweizer (Hrsg.): Lambacher-Schweizer. Mathematisches Unterrichtswerk für höhere Schulen. Geometrie. Ausgabe E. Teil 1. 15. Auflage. Ernst Klett Verlag, Stuttgart 1965. 

Weblinks

Wiktionary: Sehnenviereck – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wikibooks: Beweis des Satzes des Ptolemäus – Lern- und Lehrmaterialien

Wikibooks: Beweis zur Größe des gegenüberliegenden Winkels im Sehnenviereck – Lern- und Lehrmaterialien

• Beweis des Satzes von Ptolemäus (mit Umkehrung) mit geometrischen Mitteln der gymnasialen Mittelstufe, Landesbildungsserver Baden-Württemberg