Lagrange-Formalismus

Der Lagrange-Formalismus ist in der Physik eine 1788 von Joseph-Louis Lagrange eingeführte Formulierung der klassischen Mechanik, in der die Dynamik eines Systems durch eine einzige skalare Funktion, die Lagrange-Funktion, beschrieben wird. Der Formalismus ist (im Gegensatz zur newtonschen Mechanik, die a priori nur in Inertialsystemen gilt) auch in beschleunigten Bezugssystemen gültig. Der Lagrange-Formalismus ist invariant gegen Koordinatentransformationen. Aus der Lagrange-Funktion lassen sich die Bewegungsgleichungen mit den Euler-Lagrange-Gleichungen der Variationsrechnung aus dem Prinzip der extremalen Wirkung bestimmen. Diese Betrachtungsweise vereinfacht viele physikalische Probleme, da sich, im Gegensatz zu der newtonschen Formulierung der Bewegungsgesetze, im Lagrange-Formalismus Zwangsbedingungen relativ einfach durch das explizite Ausrechnen der Zwangskräfte oder die geeignete Wahl generalisierter Koordinaten berücksichtigen lassen. Aus diesem Grund wird der Lagrange-Formalismus verbreitet bei Mehrkörpersystemen (MKS) eingesetzt. Er lässt sich auch auf den relativistischen Fall übertragen und ist auch in der relativistischen Quantenfeldtheorie zur Formulierung von Modellen von Elementarteilchen und ihrer Wechselwirkungen weit verbreitet, behandelt dort allerdings eine feldtheoretische Version (Lagrange-Dichte).

Für Systeme mit einem generalisierten Potential und holonomen Zwangsbedingungen lautet die Lagrange-Funktion

$L=T-V$

wobei $T$ die kinetische Energie und $V$ die potentielle Energie des betrachteten Systems bezeichnen. Man unterscheidet sogenannte Lagrange-Gleichungen erster und zweiter Art. Im engeren Sinn versteht man unter dem Lagrange-Formalismus und den Lagrange-Gleichungen aber die zweiter Art, die häufig einfach als Lagrange-Gleichungen bezeichnet werden:

${\frac {\text{d}}{{\text{d}}t}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-{\frac {\partial {L}}{\partial q_{i}}}=0\,.$

Dabei sind $q_{i}$ generalisierte Koordinaten und ${\dot {q}}_{i}$ deren Zeitableitungen.

Lagrange-Gleichungen erster und zweiter Art

Mit den Lagrange-Gleichungen erster Art lassen sich die Zwangskräfte berechnen. Sie sind äquivalent zu den Gleichungen, die sich aus dem D’Alembertschen Prinzip ergeben. Wir betrachten $N$ Punktteilchen im $\ \mathbb {R} ^{3}$ mit den Ortsvektoren $\ \mathbf {r} _{i}$, $i\in \{1,...,N\}$, deren Koordinaten durch $s$ voneinander unabhängige (holonome) Zwangsbedingungen der Form $F_{k}(\mathbf {r} _{1},\ldots ,\mathbf {r} _{N},t)=0$ mit $k\in \{1,\ldots ,s\}$ eingeschränkt sind (eine explizite Zeitabhängigkeit ist erlaubt). Dadurch werden die Lagen der Teilchen auf eine $(3N-s)$-dimensionale Mannigfaltigkeit eingeschränkt ($f=3N-s$ ist die Anzahl der Freiheitsgrade).

Die auf ein Teilchen $i$ wirkenden Zwangskräfte sind proportional zum Gradienten $\nabla F_{k}$, die Gesamt-Zwangskraft $\mathbf {Z} _{i}$ ist daher

$\mathbf {Z} _{i}=\sum _{k=1}^{s}\lambda _{k}\nabla _{i}F_{k}.$

Wenn man annimmt, dass sich die äußeren Kräfte aus einem Potential ableiten lassen, kann man die Bewegungsgleichung schreiben (Lagrange-Gleichung 1. Art):

$m_{i}{\ddot {\mathbf {r} }}_{i}=-\nabla _{i}V+\sum _{k=1}^{s}\lambda _{k}\nabla _{i}F_{k},\qquad i=1,\ldots ,N$

Die $m_{i}$ sind die Massen der $N$ Punktteilchen, $V$ ist die potentielle Energie. Dies, zusammen mit den Zwangsbedingungen $F_{k}(\mathbf {r} _{1},\ldots ,\mathbf {r} _{N},t)=0$, sind $3N+s$ unabhängige Gleichungen für die $3N$ Koordinaten der $\mathbf {r} _{i}$ sowie für die $s$ Lagrange-Multiplikatoren $\lambda _{k}$. Somit ist die Lösung des Gleichungssystems eindeutig.

Bemerkung: Hier wurden nur holonome Zwangsbedingungen behandelt. Der Formalismus lässt sich aber auch auf Zwangsbedingungen der Form $\sum _{k}a_{k}\delta q_{k}=0\,$ anwenden, die z. B. bei nicht-holonomen Zwangsbedingungen zwischen den Geschwindigkeiten der Teilchen folgen. Diese Zwangsbedingungsgleichungen lassen sich im Gegensatz zu holonomen Zwangsbedingungen nicht als vollständiges Differential einer Funktion darstellen, das heißt, zwischen den Koeffizientenfunktionen gilt nicht ${\tfrac {\partial a_{i}}{\partial q_{k}}}={\tfrac {\partial a_{k}}{\partial q_{i}}}$.

Im Fall von holonomen Zwangsbedingungen kann man neue Koordinaten $q_{i}$ einführen, die diese implizit enthalten, sogenannte generalisierte Koordinaten. Mit der kinetischen Energie

$T=\sum _{i}{\frac {1}{2}}m_{i}v_{i}^{2}=\sum _{i}{\frac {1}{2}}m_{i}{\left(\sum _{j}{\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}{\dot {q}}_{j}+{\frac {\partial \mathbf {r} _{i}}{\partial t}}\right)}^{2}$

und Potentialkräften

$Q_{i}=-\nabla _{i}V=-{\frac {\partial V}{\partial q_{i}}}$

(die auch durch generalisierte Koordinaten ausgedrückt sind und dann als generalisierte Kräfte bezeichnet werden – sie haben nicht unbedingt die Dimension einer Kraft) lassen sich die Bewegungsgleichungen auch schreiben

${{\text{d}} \over {\text{d}}t}{\partial {T} \over \partial {{\dot {q}}_{i}}}-{\partial {T} \over \partial q_{i}}=Q_{i}$

oder mit der Lagrange-Funktion $L=T-V$ (Lagrange-Gleichung 2. Art):

${{\text{d}} \over {\text{d}}t}{\partial {L} \over \partial {{\dot {q}}_{i}}}-{\partial {L} \over \partial q_{i}}=0$

Treten wie in diesem Fall nur aus einem Potential ableitbare Kräfte (Potentialkräfte) auf, spricht man von konservativen Kräften.

Bemerkung: Manchmal lassen sich die generalisierten Kräfte durch ein geschwindigkeitsabhängiges generalisiertes Potential $V(q_{1},\ldots ,q_{n},{\dot {q}}_{1},\ldots ,{\dot {q}}_{n},t)$ in folgender Form schreiben

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Q_{i}=-\frac{\partial V}{\partial q_{i}}+\frac{\mathrm{d}}{\mathrm{d}t} \frac{\partial V}{\partial\dot{q}_{i}}}

Auch dann ergeben sich die Bewegungsgleichungen

${\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-{\frac {\partial L}{\partial q_{i}}}=0$,

mit der Lagrange-Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} :

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L(q_{1},\ldots,q_{n},\dot{q}_{1},\ldots,\dot{q}_{n},t)=T(q_{1},\ldots,q_{n},\dot{q}_{1},\ldots,\dot{q}_{n},t)-V(q_{1},\ldots,q_{n},\dot{q}_{1},\ldots,\dot{q}_{n},t)}

Das System ist dann aber nicht mehr im üblichen Sinn konservativ. Ein Beispiel ist das elektromagnetische Feld (siehe unten).

Manchmal hat man aber noch nicht-konservative Kräfte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Q_i^*} , so dass sich die Gleichungen schreiben:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\text{d}\over \text{d}t}{\partial{L}\over \partial{\dot{q}_i}}-{\partial{L}\over \partial q_i} = Q_i^*}

Ein Beispiel sind Systeme mit nicht-holonomen Zwangsbedingungen (siehe oben) oder Reibungskräften (zum Beispiel Rayleighsche Dissipationsfunktion).

Ableitung aus dem Hamiltonschen Prinzip

Die Lagrange-Gleichungen zweiter Art ergeben sich als sogenannte Euler-Lagrange-Gleichungen eines Variationsproblems und liefern die Bewegungsgleichungen, wenn die Lagrange-Funktion gegeben ist. Sie folgen aus der Variation des mit der Lagrange-Funktion gebildeten Wirkungsintegrals im Hamiltonschen Prinzip. Dazu betrachtet man alle möglichen Bahnkurven Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q (t)} im Raum der generalisierten Koordinaten zwischen festen Anfangs- und Endpunkten. Man betrachtet die Änderung des Wirkungsintegrals bei Variation der Bahnkurven

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \, q \rightarrow q + \delta q}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \, \dot q \rightarrow \dot q + \delta \dot q}

Das hamiltonsche Prinzip besagt, dass für die klassische Bahn das Wirkungsintegral stationär unter Variation der Bahnkurven ist:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta W = W(q+\delta q, \dot q+ \delta \dot q, t)-W(q, \dot q, t)=\delta \int \text{d}t L(q,\dot q, t) = \int \text{d}t (L (q + \delta q, \dot q + \delta \dot q, t) - L(q,\dot q, t))\stackrel{!}{=}0\,.}

Eine Näherung in erster Ordnung lautet für eine gewöhnliche Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x, y)}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x + \text{d}x, y + \text{d}y) \approx f + \frac{\partial f}{\partial x}\text{d}x + \frac{\partial f}{\partial y}\text{d}y}

also

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text{d}f = f(x + \text{d}x , y + \text{d}y) - f(x,y) = \frac{\partial f}{\partial x}\text{d}x + \frac{\partial f}{\partial y}\text{d}y} .

In erster Ordnung ergibt sich die Variation des Integrals also zu

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int \text{d}t \left(\frac{\partial L}{\partial q}\delta q + \frac{\partial L}{\partial \dot q}\delta \dot q \right) = \int \text{d}t \left(\frac{\partial L}{\partial q}\delta q + \frac{\partial L}{\partial \dot q} \frac{\text{d}}{\text{d}t} \delta q \right)} .

Nun führt man eine partielle Integration in dem Term aus, der die Ableitung nach der Zeit enthält:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_{t_1}^{t_2} \text{d}t \left(\frac{\partial L}{\partial \dot q} \frac{\text{d}}{\text{d}t} \delta q \right) = \left[\frac{\partial L}{\partial \dot q}\delta q\right]_{t_1}^{t_2} - \int_{t_1}^{t_2} \text{d}t \left( \delta q \frac{\text{d}}{\text{d}t} \frac{\partial L}{\partial \dot q} \right) } .

Hierbei wird benutzt, dass

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \,\delta q(t_1) = \delta q(t_2) = 0}

ist, da Anfangs- und Endpunkt festgehalten werden. Daher gilt für die Randterme

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left[\frac{\partial L}{\partial \dot q}\delta q\right]_{t_1}^{t_2} = 0}

Damit resultiert schließlich

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int \text{d}t \left(-\frac{\text{d}}{\text{d}t} \frac{\partial L}{\partial \dot q} + \frac{\partial L}{\partial q} \right)\delta q\mathrel{\stackrel{!}{=}} 0\,.}

Da nun Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta q} als Faktor des gesamten Integrals auftritt und beliebig ist, kann das Integral nur dann nach dem Variationsprinzip verschwinden, wenn der Integrand selbst verschwindet. Es folgen die Lagrange-Gleichungen oder Lagrange-Gleichungen zweiter Art (die Euler-Lagrange-Gleichungen des hier betrachteten Variationsproblems):

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\text{d}}{\text{d}t} \frac{\partial L}{\partial \dot{q}_i} - \frac{\partial{L}}{\partial q_i} = 0\,.}

Für jede generalisierte Koordinate Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_i} (und die zugehörige generalisierte Geschwindigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{q}_i} ) gibt es eine solche Gleichung. Die Lagrange-Gleichungen bilden ein System gewöhnlicher Differentialgleichungen zweiter Ordnung bezüglich der Zeitableitung. Wie viele Differentialgleichungen das im Endeffekt sind, weiß man erst, wenn die Zahl der Freiheitsgrade des Systems berechnet wurde.

Zyklische Variablen und Symmetrie

Wenn die Lagrange-Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} nicht von einer Koordinate Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q} abhängt, sondern nur von der zugehörigen Geschwindigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{q}} , dann nennt man Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q} zyklisch, zyklische Koordinate oder zyklische Variable. Der zur zyklischen Variablen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q} konjugierte Impuls

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p= \frac{\partial L}{\partial \dot{q}}}

ist eine Erhaltungsgröße; sein Wert ändert sich nicht während der Bewegung, wie gleich gezeigt wird: Wenn die Lagrange-Funktion nicht von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q} abhängt, gilt

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial{L}}{\partial q} = 0\,.}

Dann folgt aber aus der Euler-Lagrange-Gleichung, dass die Zeitableitung des zugehörigen konjugierten Impulses verschwindet und er somit zeitlich konstant ist:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\mathrm d}{\mathrm dt} \frac{\partial L}{\partial \dot{q}} = 0\,,}

Allgemeiner gehört nach dem Noether-Theorem zu jeder kontinuierlichen Symmetrie der Wirkung eine Erhaltungsgröße. Bei einer zyklischen Variablen ist die Wirkung invariant unter der Verschiebung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q} um eine beliebige Konstante, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q\rightarrow q+c\,.}

Erweiterung auf Felder

In der Feldtheorie ergibt sich die Bewegungsgleichung aus dem hamiltonschen Prinzip für Felder zu

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial \mathcal{L}}{\partial \phi_i} - \sum_{j=1}^3 \frac{\partial}{\partial x_j} \frac{\partial \mathcal{L}}{\partial\frac{\partial \phi_i}{\partial x_j} }- \frac{\partial}{\partial t} \frac{\partial \mathcal{L}}{\partial\frac{\partial \phi_i}{\partial t}} = \frac{\partial\mathcal L}{\partial\phi_i} - {\partial_\mu} \left(\frac{\partial\mathcal L}{\partial (\partial_\mu \phi_i )} \right) = 0}

wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \phi=\phi(x,y,z,t)} das betrachtete Feld und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathcal{L}=\mathcal{L}\left(\phi, \frac{\partial \phi}{\partial x}, \frac{\partial \phi}{\partial y}, \frac{\partial \phi}{\partial z}, \frac{\partial \phi}{\partial t}, x,y,z,t \right)} die Lagrange-Dichte sind.

Man kann dies in Kurzform auch schreiben als

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\delta \mathcal L}{\delta\phi}\equiv 0\,,}

mit der so definierten Variationsableitung   Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\delta\mathcal L}{\delta \phi}:=\frac{\partial\mathcal L}{\partial\phi_i} - {\partial_\mu} \left(\frac{\partial\mathcal L}{\partial (\partial_\mu \phi_i )} \right)} .

Hinweis: Der Lagrange-Formalismus ist auch der Ausgangspunkt vieler Formulierungen der Quantenfeldtheorie.

Relativistische Mechanik

In der relativistischen Mechanik kann die Lagrange-Funktion eines freien Teilchens aus dem hamiltonschen Prinzip abgeleitet werden, indem für die Wirkung der einfachste Fall eines relativistischen Skalars angenommen wird:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S = -m c \int\mathrm d s =- m c^2 \int \mathrm dt \sqrt{1 - \frac{v^2}{c^2}}= \int L\, \mathrm dt } ,

wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm d s = c \,\mathrm d\tau =c \, \mathrm dt \sqrt{1 - \frac{v^2}{c^2}}} das zur Eigenzeit proportionale relativistische Linienelement ist und ein konstanter Faktor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \,( - m c) } gewählt wurde.

Die Lagrange-Funktion eines freien Teilchens ist hier nicht mehr mit der kinetischen Energie identisch (manchmal spricht man deshalb auch von kinetischer Ergänzungsenergie T in der Lagrange-Funktion). Die relativistische kinetische Energie eines Körpers mit der Masse Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m} und Geschwindigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v= \dot{\mathbf{x}}} ohne Zwangsbedingungen beträgt

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E=\frac{mc^{2}}{\sqrt{1-\frac{\dot{\mathbf{x}}^{2}}{c^{2}}}\,}-mc^{2}} ,

wohingegen für die Lagrange-Funktion die kinetische Ergänzungsenergie

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T(\mathbf{x},\dot{\mathbf{x}},t)=-mc^{2}\sqrt{1-\frac{\dot{\mathbf{x}}^{2}}{c^{2}}}}

maßgeblich ist. Die Lagrange-Funktion für ein Teilchen in einem Potential V ergibt sich dann zu

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L(\mathbf{x},\dot{\mathbf{x}},t)=T-V=-mc^{2}\sqrt{1-\frac{\dot{\mathbf{x}}^{2}}{c^{2}}}\,-\, V(\mathbf{x},\dot{\mathbf{x}},t)} .

Für ein Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N} -Teilchensystem ist die Lagrange-Funktion mit den generalisierten Koordinaten

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L(q_{1},\ldots,q_{n},\dot{q}_{1},\ldots,\dot{q}_{n},t)=-\sum_{i=1}^{N}m_{0,i}c^{2}\sqrt{1-\frac{\dot{\mathbf{x}}_{i}^{2}(q_{1},\ldots,q_{n},\dot{q}_{1},\ldots,\dot{q}_{n},t)}{c^{2}}}\,-\, V(q_{1},\ldots,q_{n},\dot{q}_{1},\ldots,\dot{q}_{n},t)} ,

wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n=3N-s} die Anzahl der Freiheitsgrade und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s} die Anzahl der holonomen Zwangsbedingungen ist.

Für kleine Geschwindigkeiten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |\dot{\mathbf{x}}|\ll c} kann man die Wurzel bis zur ersten Ordnung entwickeln Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sqrt{1-x}=1-x/2} :

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle -mc^{2}\sqrt{1-\frac{\dot{\mathbf{x}}^{2}}{c^{2}}}=-mc^{2}+\frac{m}{2}\dot{\mathbf{x}}^{2}}

Die nullte Ordnung der Entwicklung ist eine Konstante, die negative Ruheenergie. Da die Lagrange-Gleichungen invariant sind unter Addition einer Konstanten zur Lagrange-Funktion, kann man den konstanten ersten Term weglassen und man erhält wieder die klassische kinetische Energie:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L(q_{1},\ldots,q_{n},\dot{q}_{1},\ldots,\dot{q}_{n},t)=\sum_{i=1}^{N}\frac{m_{0,i}}{2}\dot{\mathbf{x}}_{i}^{2}(q_{1},\ldots,q_{n},\dot{q}_{1},\ldots,\dot{q}_{n},t)\,-\, V(q_{1},\ldots,q_{n},\dot{q}_{1},\ldots,\dot{q}_{n},t)}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L(q_{1},\ldots,q_{n},\dot{q}_{1},\ldots,\dot{q}_{n},t)=T(q_{1},\ldots,q_{n},\dot{q}_{1},\ldots,\dot{q}_{n},t)\,-\, V(q_{1},\ldots,q_{n},\dot{q}_{1},\ldots,\dot{q}_{n},t)}

Zusammenhang mit Pfadintegralen in der Quantenmechanik

Richard Feynman hat als Erster diese Herangehensweise auch konsequent für die Herleitung der Gleichungen der Quantenmechanik verwendet. In der klassischen Physik ergeben sich die oben beschriebenen Lagrange-Gleichungen aus der Forderung, dass das Wirkungsintegral stationär wird. In Feynmans Pfadintegral-Formalismus ist die quantenmechanische Wahrscheinlichkeitsamplitude, dass ein System zwischen Anfangs- und Endbedingungen einen bestimmten Pfad einschlägt, proportional zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e^{\frac{i W} {\hbar}}} mit dem Wirkungsintegral Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle W} . Pfade in der Umgebung des klassischen Weges, für den die Variation von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle W} verschwindet, liefern dabei meist die Hauptbeiträge, da sich in ihrer Umgebung die Beiträge mit fast gleichen Phasenfaktoren addieren.

Beispiele

Masse im harmonischen Potential (konservativ)

Schwingungssystem: x ist die Auslenkung aus der Gleichgewichtslage

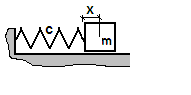
Eine Masse Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m} sei über zwei Federn mit Federkonstante Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} und festen Randbedingungen verbunden. Grundvoraussetzung zur Beschreibung des Problems im Lagrange-Formalismus ist das Aufstellen der Lagrange-Funktion, indem man die Terme für kinetische Energie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T} und potentielle Energie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V} aufstellt:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T = \frac{1}{2}m\dot{x}^2}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V = \frac{1}{2}cx^2}

Die Lagrange-Funktion lautet daher:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L = \frac{1}{2}m\dot{x}^2 - \frac{1}{2}cx^2}

Die Lagrange-Funktion wiederum wird zur analytischen Beschreibung des physikalischen Problems in die Euler-Lagrange-Gleichung eingesetzt, was dann auf Gleichungen führt, die den Bewegungsgleichungen in der Newtonschen Mechanik entsprechen. In diesem Beispiel lautet die generalisierte Koordinate Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} , die Euler-Lagrange-Gleichung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\mathrm{d}\over \mathrm{d}t}{\partial{L}\over \partial{\dot{x}}}={\partial{L}\over \partial x} } .

Dies führt mit obigen Formeln für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} auf

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ \frac{\mathrm{d}}{\mathrm{d}t}\left(m\dot{x}\right)=-c x}

und damit auf die Bewegungsgleichung des Systems:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ddot{x} = -\frac{c}{m} x} .

Die allgemeine Lösung dieser Differentialgleichung ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x(t)=A\cos(\omega t + \varphi)} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} ist die Zeit, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \textstyle \omega=\sqrt{c/m}} die Kreisfrequenz. Die konstante Amplitude Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A} und Phase Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varphi} können aus den Anfangsbedingungen bestimmt werden.

Ladung im elektromagnetischen Feld (nicht-konservativ)

Eine Punktladung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q} mit Masse Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m} bewege sich im elektromagnetischen Feld. Die generalisierten Koordinaten entsprechen den kartesischen Koordinaten in 3 Raumdimensionen.

Die Felder (Magnetfeld Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{B}} und elektrisches Feld Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{E}} ) werden über das Skalarpotential Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \phi} und das Vektorpotential Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{A}} bestimmt:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{B}(\mathbf{x},t)=\nabla\times\mathbf{A}(\mathbf{x},t)\ ,\quad\mathbf{E}(\mathbf{x},t)=-\frac{\partial\mathbf{A}(\mathbf{x},t)}{\partial t}-\nabla\phi(\mathbf{x},t)}

Die kinetische Energie des Teilchens ist klassisch:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T(\dot{\mathbf{x}})=\frac{1}{2}m\dot{\mathbf{x}}^{2}}

Das „Potential“ ist hier allerdings geschwindigkeitsabhängig, man spricht deshalb wie oben dargestellt von einem generalisierten Potential:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V(\mathbf{x},\dot{\mathbf{x}},t)=q\left(\phi(\mathbf{x},t)-\dot{\mathbf{x}}\cdot\mathbf{A}(\mathbf{x},t)\right)}

Somit ist die Lagrange-Funktion eines geladenen Teilchens im elektromagnetischen Feld:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L(\mathbf{x},\dot{\mathbf{x}},t)=\frac{1}{2}\, m\,\dot{\mathbf{x}}^{2}-q\,\phi(\mathbf{x},t)+q\,\dot{\mathbf{x}}\cdot\mathbf{A}(\mathbf{x},t)}

Die Euler-Lagrange-Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{d}{dt}\nabla_{\dot{\mathbf{x}}}L-\nabla_{\mathbf{x}}L=0} führt auf die Bewegungsgleichung, auf deren rechter Seite die Lorentzkraft steht:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m\,\ddot{\mathbf{x}}=q\,\dot{\mathbf{x}}\times\left(\nabla\times\mathbf{A}(\mathbf{x},t)\right)-q\,\frac{\partial}{\partial t}\mathbf{A}(\mathbf{x},t)-q\,\nabla\phi(\mathbf{x},t)}

Masse an Trommel (nicht-konservativ)

Datei:Aufzug lg.png

Schema eines Aufzuges

Die Achse einer Aufzugtrommel wird durch ein Drehmoment Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M} angetrieben. Die Masse der Last beträgt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m} , das Massenträgheitsmoment der Trommel ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J} . Der Radius der Trommel ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r} .

Zwischen den Koordinaten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varphi} besteht folgende Beziehung:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x = r \varphi}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow \;\dot{x} = r \dot{\varphi}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow \;\delta x = r \delta \varphi}

Die kinetische Energie ist:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T = \frac{1}{2} \left( m \dot{x}^2 + J \dot{\varphi}^2 \right) = \frac{1}{2} \left( m r^2 + J \right)\ \dot{\varphi}^2 }

Die virtuelle Arbeit der eingeprägten Kräfte ist

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta W = -mg\,\delta x + M\,\delta \varphi = (-mgr + M)\,\delta \varphi}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow \;Q = -mgr + M}

Daraus folgt schließlich die Bewegungsgleichung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left( m r^2 + J \right) \ddot{\varphi} = -mgr + M}

Die Auflösung dieser Gleichung nach der Winkelbeschleunigung ergibt

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ddot {\varphi}=\frac{-mgr + M}{ m r^2 + J }}

Atwoodsche Fallmaschine (Methode erster Art)

Funktionsschema der Fallmaschine

→ Hauptartikel: Atwoodsche Fallmaschine

Bei der Atwoodschen Fallmaschine betrachtet man zwei Punktmassen im Gravitationsfeld der Erde, die über eine Rolle in der Höhe h aufgehängt und durch ein Seil der Länge l verbunden seien. Die Zwangsbedingung lautet in diesem Fall:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \, F:=y_1 + y_2 + l - 2h = 0}

Wird das Seil berücksichtigt, das auf der Rolle (Rollenradius r) liegt, dann ergibt sich:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F:=y_1 + y_2 + l - 2h - \pi\ r = 0}

Die potentielle Energie V berechnet sich zu:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V := m_1 g y_1 + m_2 g y_2}

Für die Gradienten erhält man

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial F}{\partial y_1 } = 1,\qquad \frac{\partial F}{\partial y_2 } = 1}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial V}{\partial y_1 } = m_1 g,\qquad \frac{\partial V}{\partial y_2 } = m_2 g}

Dies führt auf das System der Lagrange-Gleichungen 1. Art:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{matrix} m_1 \ddot y_1 &=& - m_1 g + \lambda\\ m_2 \ddot y_2 &=& - m_2 g + \lambda\\ y_1 + y_2 + l - 2h &=& 0 \end{matrix} }

Dies kann man auflösen und erhält z. B. für bekannte Anfangsbedingungen:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{matrix}y_1(t) &=& \frac {1}{2}{m_2 - m_1 \over {m_1 + m_2}} g t^2 + \dot y_{1,0}t + y_{1,0}\\ \lambda &=& 2 g \frac{m_1 m_2}{m_1 + m_2}\end{matrix}}

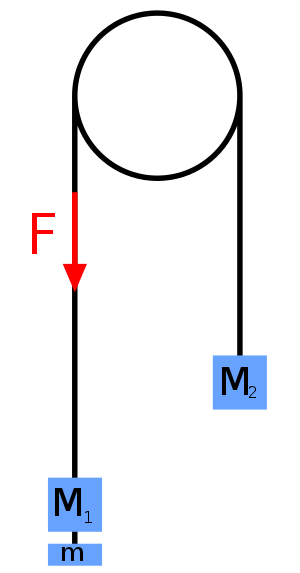
Mit einem Seil verbundene Teilchen auf einer Platte mit Loch (Zweikörperproblem mit Methode 2. Art)

Die 1. Masse (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_1 } ) ist auf einer dünnen Platte durch ein Loch in der Mitte der Platte durch ein Seil mit konstanter Länge (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l} ) mit einer 2. Masse (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_2 } ) verbunden, die sich nur in z-Richtung bewegt (die z-Achse zeige in Richtung Erdmittelpunkt).

Die Zwangsbedingungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_i } lauten:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_1 = z_1 = 0;\quad g_2 = x_2 = 0;\quad g_3 = y_2 = 0;\quad g_4 = \sqrt{x_1^2+y_1^2} + z_2 - l = 0 }

Aus 4 Zwangsbedingungen bei 2 Massen im Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \R^3 } ergeben sich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 6-4=2 } Freiheitsgrade. Für dieses Problem empfiehlt es sich aufgrund der Azimutalsymmetrie Zylinderkoordinaten zu verwenden. So können die generalisierten Koordinaten einfach bestimmt werden.

In Zylinderkoordinaten können die beiden generalisierten Koordinaten nun als

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_1 = r_1 = \sqrt{x_1^2+y_1^2}, \qquad q_2 = \phi_1 = \arctan \frac{y_1}{x_1}}

gewählt werden, wobei mittels der 4. Zwangsbedingung auch die Bewegung der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_2 } durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_1 } beschrieben wird;

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_4 = r_1 + z_2 - l = 0 \Leftrightarrow z_2 = l - r_1}

Die kinetische Energie des Systems lautet nun

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_\mathrm{kin} = \frac{m_{1} + m_{2}}{2} \dot{r}_1^2 +\frac{m_1}{2} r_1^2 \dot{\phi}_1^2} .

Da Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z_1 = 0 } und sich damit nur die potentielle Energie bei der 2. Masse verändert, lautet sie

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_\mathrm{pot} = m_2 g r_1} .

Daraus folgt dann die Lagrangefunktion

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L = T-V = \frac{m_1 + m_2}{2} \dot r_1^2 +\frac{m_1}{2} r_1^2 \dot \phi_1^2 - m_2 g r_1 }

Da bei dieser Problemstellung zwei generalisierte Koordinaten vorliegen, folgt jeweils eine Bewegungsgleichung für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_1} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \phi_1} :

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial L}{\partial r_1} = m_1 r_1 \dot \phi_1^2 - m_2 g; \quad \frac{\mathrm d}{\mathrm dt} \frac{\partial L}{\partial \dot r_1} = \frac{\mathrm d}{\mathrm dt} (m_{1}+m_{2})\dot r_1 = (m_{1} + m_{2}) \ddot r_1 \quad \Rightarrow \quad (m_1 + m_2)\ddot r_1 = m_1 r_1 \dot \phi_1^2 - m_2 g }

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial L}{\partial \phi_1} = 0; \quad \frac{\mathrm d}{\mathrm dt} \frac{\partial L}{\partial \dot \phi_1} = \frac{\mathrm d}{\mathrm dt} m_1 r_1^2 \dot \phi_1 = 2 m_1 r_1 \dot r_1 \dot \phi_1 + m_1 r_1^2 \ddot \phi_1 \quad \Rightarrow \quad 2 m_1 r_1 \dot r_1 \dot \phi_1 + m_1 r_1^2 \ddot \phi_1 = 0}

Aus der Gleichung für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \phi} zeigt sich in der Form

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\mathrm d}{\mathrm dt} m_1 r_1^2 \dot \phi_1 = 0}

die Existenz einer Erhaltungsgröße, des Drehimpulses in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z} -Richtung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L_1^z = m_1 r_1^2 \dot \phi_1} , der nach dem Noether-Theorem aus der Unabhängigkeit der Lagrangefunktion von der Variablen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_2 = \phi_1} folgt.

Teilchen im freien Fall (allgemeine Relativitätstheorie)

In der allgemeinen Relativitätstheorie durchlaufen frei fallende Teilchen Weltlinien längster Zeit: Zwischen zwei (genügend nah beieinander liegenden) Ereignissen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B} vergeht auf einer mitgeführten Uhr auf der Weltlinie frei fallender Teilchen mehr Zeit als auf allen anderen Weltlinien durch diese Ereignisse. Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s} ein entlang des Pfades monoton wachsender Laufparameter, so ergibt sich die verstrichene Zeit zu

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tau_{AB} = \int_{\underline{s}}^{\overline{s}}L\left(s, x(s), \frac{\mathrm dx}{\mathrm ds}\right)\,\mathrm d s\ ,\ x(\underline{s}) = A\,,\ x(\overline{s}) = B\,,}

mit der Lagrange-Funktion

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L(s,x,\dot{x}) = \sqrt{g_{mn}(x)\, \dot{x}^m \,\dot{x}^n}\,.}

Dabei sind Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_{mn}(x)} die Komponentenfunktionen der Metrik (sowohl Raum- als auch Zeitkomponenten). Wir rechnen einfachheitshalber in Maßsystemen, in denen die Lichtgeschwindigkeit dimensionslos ist und den Wert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c=1} hat, und verwenden die Einsteinsche Summenkonvention.

Der zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^k} konjugierte Impuls ist

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial L}{\partial \dot{x}^k}=\frac{g_{kl}\,\dot{x}^l}{\sqrt{g_{mn}\,\dot{x}^m \,\dot{x}^n}}}

und die Euler-Lagrange-Gleichungen lauten

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0=\frac{\mathrm d }{\mathrm ds} \frac{g_{kl}\,\dot{x}^l}{\sqrt{g_{mn}\,\dot{x}^m\,\dot{x}^n}} - \frac{1}{2} \frac{\partial_k g_{rs}\,\dot{x}^r\,\dot{x}^s}{\sqrt{g_{mn}\,\dot{x}^m \,\dot{x}^n}} }

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \qquad\qquad =g_{kl}\,\frac{\mathrm d }{\mathrm ds} \frac{\dot{x}^l}{\sqrt{g_{mn}\,\dot{x}^m\,\dot{x}^n}} + \frac{\dot{x}^r\,\partial_r g_{ks}\,\dot{x}^s}{\sqrt{g_{mn}\,\dot{x}^m \,\dot{x}^n}} - \frac{1}{2} \frac{\partial_k g_{rs}\,\dot{x}^r\,\dot{x}^s}{\sqrt{g_{mn}\,\dot{x}^m \,\dot{x}^n}}\,. }

Verwenden wir hier als Abkürzung das Christoffel-Symbol

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Gamma^l_{rs} = \frac{1}{2}g^{lm}\bigl(\partial_r g_{sm}+\partial_s g_{rm}-\partial_m g_{rs}\bigr)\,,}

so erweist sich die Weltlinie längster Dauer als Gerade: Die Richtung der Tangente an die Weltlinie

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle u^l = \frac{\dot{x}^l}{\sqrt{g_{mn}\,\dot{x}^m \,\dot{x}^n}}}

ändert sich nicht bei Parallelverschiebung längs der Weltlinie

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0=g_{kl}\left(\frac{\mathrm d }{\mathrm ds} u^l + \dot{x}^r\, \Gamma^l_{rs}\,u^s\right)\,. }

Die Parametrisierung wird nicht festgelegt. Verfügen wir so über sie, dass der Tangentialvektor überall gleich lang ist, dann ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sqrt{g_{mn}\,\dot{x}^m \,\dot{x}^n}} konstant und der Tangentialvektor geht beim Durchlaufen der Weltlinie in sich über. Sie erfüllt die Geodätengleichung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0=\frac{\mathrm d^2 x^l }{\mathrm ds^2} + \Gamma^l_{rs}(x)\, \frac{\mathrm d x^r}{\mathrm d s}\,\frac{\mathrm d x^s}{\mathrm d s}\,. }

Dies ist die allgemein-relativistische Form der Bewegungsgleichung eines frei fallenden Teilchens. Die Gravitation ist in den Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Gamma^l_{rs}} voll berücksichtigt.

Literatur

Der Lagrange-Formalismus wird in vielen ein- und weiterführenden Lehrbüchern der klassischen Mechanik behandelt.

• Josef Honerkamp, Hartmann Römer: Klassische Theoretische Physik. 3. Auflage. Springer, 1993, ISBN 3-540-55901-9.  (Volltext hier erhältlich)
• Herbert Goldstein, Charles P. Poole, John L. Safko: Klassische Mechanik. 3. Auflage. Wiley-VCH, 2006, ISBN 3-527-40589-5. 
• Cornelius Lanczos: The Variational Principles of Mechanics. 4. Auflage. Dover Publ. Inc, 1986, ISBN 0-486-65067-7. 
• Friedhelm Kuypers: Klassische Mechanik. 8. Auflage. Wiley-Vch, 2008, ISBN 3-527-40721-9. 

Literatur zu Pfadintegralen.

• Hagen Kleinert: Pfadintegrale in Quantenmechanik, Statistik und Polymerphysik. Spektrum, Mannheim 1993, ISBN 3-86025-613-0. 

Weblinks

• Whittaker Analytische Dynamik der Punkte und starren Körper, Springer, Grundlehren der mathematischen Wissenschaften 1924
• Artikel Von d´Alembert zu Lagrange II auf matheplanet.com
• Anwendungen des Lagrange-Formalismus an Beispielen der Oberstufenphysik