Laser

Laser (/ˈlɛɪzər/, auch /ˈleːzər/ oder /ˈlaːzər/; Akronym für englisch light amplification by stimulated emission of radiation ‚Licht-Verstärkung durch stimulierte Emission von Strahlung‘) bezeichnet sowohl den physikalischen Effekt als auch das Gerät, mit dem Laserstrahlen erzeugt werden.

Laserstrahlen sind elektromagnetische Wellen. Vom Licht einer zur Beleuchtung verwendeten Lichtquelle, beispielsweise einer Glühlampe, unterscheiden sie sich vor allem durch die sonst unerreichte Kombination von hoher Intensität, oft sehr engem Frequenzbereich (monochromatisches Licht), scharfer Bündelung des Strahls und großer Kohärenzlänge. Auch sind, bei sehr weitem Frequenzbereich, extrem kurze und intensive Strahlpulse mit exakter Wiederholfrequenz möglich.

Laser haben zahlreiche Anwendungsmöglichkeiten in Technik und Forschung sowie im täglichen Leben, vom einfachen Lichtzeiger (z. B. Laserpointer bei Präsentationen) über Entfernungsmessgeräte, Schneid- und Schweißwerkzeuge, Auslesen von optischen Speichermedien wie CDs, DVDs und Blu-ray Discs, Nachrichtenübertragung bis hin zum Laserskalpell und anderen Laserlicht verwendenden Geräten im medizinischen Alltag.

Laser gibt es für Strahlungen in verschiedenen Bereichen des elektromagnetischen Spektrums: von Mikrowellen (Maser) über Infrarot (dann auch IRASER genannt), sichtbares Licht, Ultraviolett bis hin zu Röntgenstrahlung. Die besonderen Eigenschaften der Laserstrahlen entstehen durch ihre Erzeugung in Form einer stimulierten Emission. Der Laser arbeitet wie ein optischer Verstärker, typischerweise in resonanter Rückkopplung. Die dazu erforderliche Energie wird von einem Lasermedium (bspw. Kristall, Gas oder Flüssigkeit) bereitgestellt, in dem aufgrund äußerer Energiezufuhr eine Besetzungsinversion herrscht. Die resonante Rückkopplung entsteht in der Regel dadurch, dass das Lasermedium sich in einem elektromagnetischen Resonator für die Strahlung bestimmter Richtung und Wellenlänge befindet.

Neben den diskreten Energieniveaus atomarer Übergänge gibt es auch Laserbauarten mit kontinuierlichen Energieübergängen wie den Freie-Elektronen-Laser. Da atomare Energieniveaus kleiner 13,6 eV beschränkt sind, dies entspricht einer Grenze bei der Wellenlänge von 90 nm, benötigen die im Bereich der Röntgenstrahlung mit Wellenlängen kleiner 10 nm arbeitenden Röntgenlaser Bauarten mit kontinuierlichen Energieübergängen.

Verschiedenfarbige Laser

Demonstrationslaser: In der Mitte ist das Leuchten der Gasentladung zu sehen, die das Lasermedium anregt. Der Laserstrahl ist rechts als roter Punkt auf dem weißen Schirm zu erkennen.

Grundfunktionen

Grundlegende Bestandteile

Ein Laser besteht konzeptionell aus drei Bestandteilen:

Aktives Medium (Lasermedium)

Im aktiven Medium entstehen durch den optischen Übergang angeregter Atome oder Moleküle in einen energetisch günstigeren Zustand Photonen. Zentrale Bedingung für ein Lasermedium ist, dass sich eine Besetzungsinversion herstellen lässt. Das bedeutet, dass der obere Zustand des optischen Übergangs mit einer höheren Wahrscheinlichkeit besetzt ist als der untere. Ein solches Medium muss mindestens über drei Niveaus verfügen und kann gasförmig (z. B. CO₂), flüssig (z. B. Farbstofflösungen) oder fest (z. B. Rubinkristall, Halbleitermaterial) sein.

Pumpe

Um eine Besetzungsinversion herbeizuführen, muss in das Lasermedium Energie hineingepumpt (englisch pumping) werden. Damit dieser Pumpprozess nicht mit der stimulierten Emission konkurriert, muss dieser auf einem anderen quantenmechanischen Übergang basieren. Das Pumpen kann optisch (Einstrahlung von Licht) oder elektrisch (z. B. Gasentladung, elektrischer Strom bei Laserdioden) die Atome oder Moleküle des Lasermediums in angeregte Zustände bringen.

Resonator

Ein Resonator besteht zum Beispiel aus zwei parallelen Spiegeln, zwischen welchen sich das aktive Lasermedium befindet. Photonen, deren Propagation senkrecht zu den Spiegeln verläuft, verbleiben im Resonator und können daher mehrfach die Emission weiterer Photonen im aktiven Medium auslösen (stimulieren). Ein auf diese Weise entstehendes Photon entspricht in allen Quantenzahlen dem auslösenden Photon. Spontane Photonen, die den Resonator zum Beispiel quer verlassen, stimulieren dementsprechend eher keine weiteren Photonen. Diese Selektion des Resonators führt zur engen Abstrahlrichtung von Laserstrahlung. Manche Resonatoren sind auch wellenlängenselektiv (dichroitische Spiegel, Bragg-Gitter) und können dadurch die anschwingenden longitudinalen Moden weiter einschränken. In manchen hochverstärkenden Lasermedien ist ein Resonator zum Erzielen stimulierter Emission nicht zwingend erforderlich (siehe Superstrahler).

Funktionsweise

Zunächst werden Atome im Lasermedium durch die eingespeiste Leistung von unteren Energieniveaus (z. B. Grundzustand) in energetisch höhere, d. h. angeregte Zustände versetzt. Dabei soll die mittlere Zerfallszeit der angeregten Zustände (in der Regel durch spontane Emission) möglichst lang sein. Somit bleibt die Pumpenergie dort „längere“ Zeit gespeichert, sodass eine Besetzungsinversion aufgebaut werden kann. Nun genügt eine Stimulierung eines Atoms durch ein Photon mit der auszustrahlenden Energie, damit das angeregte Atom wieder in seinen Grundzustand zurückfällt und dabei ein Photon der identischen Energie (also identischer Wellenlänge und Frequenz) sowie identischer Phasenlage wie das stimulierende Photon aussendet. Beide Photonen bewegen sich in die gleiche Richtung. Durch diese Verdoppelung des stimulierenden Photons wirkt das Lasermedium wie ein Lichtverstärker. Das „frisch entstandene“ zweite Photon kann dann seinerseits andere angeregte Atome zur Ausstrahlung stimulieren, und es kommt zu einer Kettenreaktion.

Zu dieser Verstärkerwirkung kommt dann noch hinzu, dass sich die Anordnung in einem Resonator (s. u. bei Laserresonator) befindet, der durch seine Abmessungen auf die gewünschte Wellenlänge abgestimmt ist. So hat ein Photon bei mehrfachem Durchlaufen des Lasermediums genügend Chancen, andere Atome zu stimulieren. Der Resonator ist im Prinzip aus zwei Spiegeln an den Enden der Anordnung gebildet. Durch diese Spiegel wird auch die Richtung des erzeugten Lichtstrahls endgültig festgelegt. Einer der beiden Spiegel ist teildurchlässig ausgeführt, so dass ein Teil des Lichts austreten und seiner Nutzung zugeführt werden kann.

Geschichte

Albert Einstein beschrieb bereits 1916 die stimulierte Emission als eine Umkehrung der Absorption. 1928 gelang Rudolf Ladenburg der experimentelle Nachweis. Danach wurde lange gerätselt, ob der Effekt zur Verstärkung des Lichtfeldes benutzt werden könnte, da zum Erreichen der Verstärkung eine Besetzungsinversion eintreten musste. Diese ist aber in einem stabilen Zweiniveausystem unmöglich. Zunächst wurde ein Dreiniveausystem in Betracht gezogen, und die Rechnungen ergaben eine Stabilität für Strahlung im Mikrowellenbereich, 1954 realisiert im Maser von Charles H. Townes, der Mikrowellenstrahlung aussendet. Danach wurde unter anderem auch von Townes und Arthur L. Schawlow an der Übertragung des Maserprinzips auf kürzere Wellenlängen gearbeitet. Optisches Pumpen wurde Anfang der 1950er Jahre von Alfred Kastler eingeführt. In den 1950er Jahren entdeckten auch die sowjetischen Wissenschaftler und Nobelpreisträger Alexander Michailowitsch Prochorow und Nikolai Gennadijewitsch Bassow unabhängig das Maserprinzip und Optisches Pumpen und Prochorow schlug 1958 die Realisierung bei kürzeren Wellenlängen in einem Rubinlaser vor. Der erste Laser – ein Rubinlaser – wurde von Theodore Maiman am 16. Mai 1960 fertiggestellt. Der erste Gaslaser, der Helium-Neon-Laser, wurde ebenfalls 1960 entwickelt (Ali Javan, William R. Bennett, Donald R. Herriott).

Geprägt wurde der Begriff Ende der 1950er Jahre durch Gordon Gould in Anlehnung an den Maser; Gould nutzte den Begriff erstmals 1957 in seinen Notizen. Frühe Veröffentlichungen nannten den Laser noch

optical maser

(optischer Maser).

Die weitere Entwicklung führte dann zunächst zu verschiedenen Gaslasern (Sauerstoff-, Stickstoff-, CO₂-Laser, He-Ne-Laser) und danach zu Farbstofflasern (das laseraktive Medium ist flüssig) durch Fritz P. Schäfer und Peter Sorokin (1966). Eine Weiterentwicklung von Kristalltechnologien ermöglichte eine sehr starke Erweiterung des spektralen Nutzbereiches. Durchstimmbare Laser zum Anfahren einer bestimmten Wellenlänge und breitbandige Laser wie z. B. der Titan-Saphir-Laser läuteten in den 1980er Jahren die Ära der Ultrakurzpulslaser mit Pulsdauern von Piko- und Femtosekunden ein.

Die ersten Halbleiterlaser wurden in den 1960er Jahren entwickelt (Robert N. Hall 1962, Nick Holonyak 1962 im sichtbaren Spektralbereich, Nikolai Bassow), praktikabel aber erst mit der Entwicklung von Halbleiterlasern auf Basis von Heterostrukturen (Nobelpreis für Herbert Kroemer, Schores Alfjorow). In den späten 1980er Jahren ermöglichte die Halbleitertechnik immer langlebigere, hocheffektive Halbleiter-Laserdioden, die mit kleiner Leistung in CD- und DVD-Laufwerken oder in Glasfaser-Datennetzen eingesetzt werden und inzwischen nach und nach als Pumpquellen mit Leistungen bis in den kW-Bereich die wenig effektive Lampenanregung von Festkörperlasern ersetzen.

In den 1990er Jahren wurden neue Pumpgeometrien für hohe Laserleistungen verwirklicht, wie der Scheiben- und der Faserlaser. Letztere fanden zur Jahrtausendwende aufgrund der Verfügbarkeit von neuen Fertigungstechniken und Leistungen bis 20 kW zunehmend Anwendungen bei der Materialbearbeitung, bei der sie die bisher gebräuchlichen Typen (CO₂-Laser, lampengepumpte Nd:YAG-Laser) teilweise ersetzen können. Ende der 1990er Jahre erreichten blaue und ultraviolette Laserdioden die Marktreife (Shuji Nakamura).

Zu Beginn des 21. Jahrhunderts wurden erstmals nichtlineare Effekte ausgenutzt, um Attosekundenpulse im Röntgenbereich zu erzeugen. Damit ließen sich zeitliche Abläufe im Inneren eines Atoms verfolgen. Inzwischen ist der Laser zu einem bedeutenden Instrument der Industrie, Medizin, Kommunikation, Wissenschaft und Unterhaltungselektronik geworden.

Physikalische Grundlagen

Im aktiven Medium im Resonator befindet sich eine feste Anzahl Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N } Atome oder Moleküle mit jeweils mehreren, aber immer den gleichen, Energieniveaus. Zwei dieser Niveaus, bezeichnet als unteres Laserniveau $E_{1}$ und oberes Laserniveau $E_{2}$ (wobei $E_{1}<E_{2}$), bilden den Laserübergang. Der Laserübergang ist derjenige optische Übergang, dessen Energiedifferenz der Frequenz des Laserlichts entspricht. Die Differenz $\Delta N=N_{1}-N_{2}$ zwischen der Anzahl der Teilchen im unteren $N_{1}$ und oberen Laserniveau $N_{2}$ wird als „Inversion“ bezeichnet und ist maßgeblich für die Funktionsweise des Lasers.

Es existieren zwei grundlegende Bedingungen, die gleichzeitig erfüllt sein müssen, damit ein Laser funktioniert:

1. $\Delta N<0$ (Besetzungsinversion) – es müssen sich mehr Teilchen im oberen als im unteren Laserniveau befinden.
2. Sofern ein Resonator verwendet wird, muss die Verstärkung des Laserlichts durch stimulierte Emission bei einem Durchlauf durch den Resonator größer als seine Verluste durch Absorption, Streuung und Spiegelverluste, insbesondere Auskoppelverluste, sein. Die Resonatorspiegel müssen wenigstens auf einer Seite eine Reflektivität kleiner eins haben, damit Laserlicht den Laser verlassen kann und überhaupt genutzt werden kann. Dieses Auskoppeln eines Teils des Laserlichts wird als Auskoppelverlust bezeichnet, weil dieser Anteil nicht mehr zur weiteren Verstärkung im Lasermedium durch stimulierte Emission beiträgt.

Jeder Übergang zwischen den zwei Niveaus entspricht der Emission oder Absorption eines Photons mit der Kreisfrequenz $\omega =\Delta E/\hbar$, wobei $\Delta E$ die Energiedifferenz zwischen den beiden Niveaus und $\hbar$ das reduzierte Plancksche Wirkungsquantum ist. Bei der Emission entsteht solch ein Photon, bei Absorption geht entsprechend ein Photon verloren. Die Wahl des Lasermediums gibt somit die Frequenz bzw. die Farbe des Lichtes vor.

Die mathematische Beschreibung der Besetzung erfolgt über spezielle gekoppelte Differentialgleichungen, sogenannte Ratengleichungen. Diese beschreiben den zeitlichen Verlauf der Besetzungszustände, also die zeitliche Änderung von $N_{1}$ und $N_{2}$. Die genaue Form der Ratengleichungen hängt davon ab, wie viele Energieniveaus neben den zwei Laserniveaus zur Verfügung stehen und genutzt werden sowie von der Art bestimmter Näherungen.

Zweiniveausystem

→ Hauptartikel: Zweizustandssystem

Ein Zweiniveausystem

Zwei stabile Energieniveaus reichen nicht für die Konstruktion eines Lasers aus, wie im Folgenden gezeigt wird. Die Betrachtung von Zweiniveausystemen liefert jedoch die Grundlage für Betrachtungen von Lasermedien mit mehr als zwei Energieniveaus, bei denen Laserbetrieb möglich ist. Ein theoretisches Zweiniveausystem würde direkt vom unteren in das obere Laserniveau gepumpt werden. Für ein Zweiniveausystem lauten die Ratengleichungen:

${\frac {dN_{1}}{dt}}=-BIN_{1}+BIN_{2}+AN_{2}$

${\frac {dN_{2}}{dt}}=+BIN_{1}-BIN_{2}-AN_{2}=-{\frac {dN_{1}}{dt}}$

Dabei ist $A$ der Einsteinkoeffizient für die spontane Emission, $B$ der Einsteinkoeffizient für Absorption bzw. stimulierte Emission und $I$ die Intensität des Lichts im Resonator. Die einzelnen Terme stehen jeweils für die Absorption bzw. Emission von Photonen und damit die Änderung der Teilchenzahl in diesem Zustand. Da für den Laserbetrieb die Inversion $\Delta N$ wichtig ist, wird die Differenz dieser zwei Ratengleichungen gebildet, sowie $N_{1}$ und $N_{2}$ durch $\Delta N=N_{1}-N_{2}$ und die Erhaltungsgröße $N=N_{1}+N_{2}$ ausgedrückt:

${\frac {d(N_{1}-N_{2})}{dt}}={\frac {d\Delta N}{dt}}=-2BI\Delta N+AN-A\Delta N$

Nach einer gewissen Zeit wird sich ein Gleichgewicht in den Besetzungen einstellen, wodurch die zeitliche Änderung der Inversion verschwindend klein wird (Fixpunkt). Um diesen Gleichgewichtspunkt zu finden, setzt man ${\tfrac {d\Delta N}{dt}}=0.$ Die sich ergebende Gleichung kann dann nach $\Delta N^{s}$ umgeformt werden:

$\Delta N^{s}={\frac {N}{1+2I/I_{S}}},$

wobei $I_{S}=A/B$ als Sättigungsintensität bezeichnet wird (der Index $S$ steht für „stationär“). Diese Besetzungsinversion ist immer positiv, unabhängig davon, wie groß die Intensität $I$ wird. Das heißt, es sind immer weniger Teilchen im oberen Laserniveau als im unteren. Somit ist eine Besetzungsinversion in einem stabilen Zweiniveausystem nicht möglich. Es ist somit unmöglich, in dieser Weise einen Laser zu konstruieren.

Eine anschauliche Begründung liefern die Einsteinkoeffizienten. Sobald die Hälfte aller Teilchen im Lasermedium im oberen Laserniveau sind, ist die Wahrscheinlichkeit, dass ein Atom im unteren Laserniveau ein Photon absorbiert, genauso hoch wie die Wahrscheinlichkeit, dass ein Atom im oberen Laserniveau ein Photon durch stimulierte Emission abgibt. Die zusätzliche spontane Emission sorgt weiterhin dafür, dass nicht einmal diese theoretische Grenze erreicht wird.

Dreiniveausystem

Zusätzlich zu den beiden Niveaus im Zweiniveausystem existiert in einem Dreiniveausystem ein weiteres Energieniveau $E_{3}$ oberhalb des oberen Laserniveaus, so dass gilt $E_{1}<E_{2}<E_{3}$. Das Pumpen erfolgt diesmal vom unteren Laserniveau $E_{1}$ in das neue Niveau $E_{3}$. Für das dritte Niveau wird außerdem die Bedingung aufgestellt, dass es viel schneller in den Zustand $E_{2}$ übergeht als $E_{2}$ nach $E_{1}$, so dass gilt $N_{3}\approx 0$ oder wieder $N=N_{1}+N_{2}+N_{3}\approx N_{1}+N_{2}$. Dieser schnelle Übergang geschieht entweder strahlungslos oder über spontane Emission. Analog zum Zweiniveausystem werden auch hier wieder Ratengleichungen aufgestellt:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{dN_1}{dt} = -BIN_1 + AN_2}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{dN_2}{dt} = +BIN_1 - AN_2 = -\frac{dN_1}{dt}}

Im Gegensatz zum Zweiniveausystem fehlt hier die stimulierte Emission durch den Pumpvorgang. Wieder können diese Ratengleichungen durch Differenzbildung, Ausdrücken durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta N} und $N$ und anschließender Betrachtung des Gleichgewichtszustandes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tfrac{d\Delta N}{dt} = 0} zu einer Gleichung für die Besetzung umgeformt werden:

$\Delta N^{s}=N{\frac {1-I/I_{S}}{1+I/I_{S}}}$

Diese Gleichung wird negativ (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_1 < N_2} ), sobald die Bedingung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I > I_S} erfüllt wird. Dies bedeutet, dass sich in einem Dreiniveausystem mehr Teilchen im oberen Laserniveau befinden können und somit Besetzungsinversion möglich ist. Voraussetzung ist eine hohe Intensität des Lichts im Resonator. Dreiniveaulaser sind somit möglich.

Vierniveausystem

Bei einem Vierniveausystem kommt gegenüber dem Dreiniveausystem ein weiteres Energieniveau $E_{0}$ hinzu. Dieses befindet sich unterhalb des unteren Laserniveaus Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_1} , so dass gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_0 < E_1 < E_2 < E_3} . Der Übergang von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_1} nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_0} hat wieder als Bedingung, dass er sehr schnell geschieht. Damit ändert sich die genäherte Bedingung für die Gesamtteilchenzahl zu $N\approx N_{0}+N_{2}$, und die Gleichung für die Besetzung wird zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta N = N_1 - N_2 \approx - N_2} . Der Pumpvorgang geschieht hierbei von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_0} nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_3} . Die Ratengleichungen ergeben sich damit zu:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{dN_1}{dt} \approx 0}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{dN_2}{dt} = +BIN_0 - AN_2}

Auch hier ist es wieder möglich, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_0} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_2} durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta N} auszudrücken sowie die Gleichgewichtsbedingung anzusetzen und nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta N} aufzulösen:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta N = -N\frac{I/I_S}{1 + I/I_S}}

In diesem Fall ist die Besetzung immer negativ. Das bedeutet, dass ein extern angeregtes Vierniveausystem sehr gut als Lasermedium geeignet ist. Praktisch alle modernen Laser werden als Vier- oder Mehrniveausysteme konzipiert.

Laserresonator

Schema eines Laserresonators

Strahlenverlauf im konfokalen Resonator

In einem Laser wird die Strahlung, die anfänglich durch spontane Emission initiiert wurde, durch eine geeignete Anordnung zweier Spiegel immer wieder durch das Gebiet geleitet, in dem Besetzungsinversion herrscht. Eine solche Anordnung heißt optischer Resonator oder Laserresonator. Durch das ständige Hin- und Herlaufen kann eine ausreichende Verstärkung zur Überschreitung der Laserschwelle erreicht werden. Die Laserschwelle kann nur überschritten werden, wenn die Verstärkung im Resonator größer ist als der Verlust (z. B. durch spontane Emission, Streuung und ausgekoppelter Leistung). Diese Bedingung stellt neben der Besetzungsinversion die zweite grundlegende Voraussetzung dar, dass ein Laser funktionieren kann.

Ein Laserresonator besteht im einfachsten Fall aus zwei Spiegeln, zwischen denen die Strahlung reflektiert wird, so dass sich der Weg durch das Lasermedium verlängert. Dadurch kann ein Photon sehr oft stimulierte Emission hervorrufen. Einer der beiden Spiegel ist teildurchlässig und wird Auskoppelspiegel oder Auskoppler genannt. Dieser sorgt dafür, dass ein Teil der Strahlung das Gerät als Laserstrahl verlassen kann. Lasermedien mit sehr hoher Verstärkung können unter Umständen auch mit nur einem Spiegel oder ganz ohne Spiegel arbeiten.

Im Resonator werden nur Frequenzen verstärkt, welche die Resonanzbedingung erfüllen, für die also gilt:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L = n \frac{\lambda}{2} \quad\Leftrightarrow\quad \nu = n \frac{c}{2L}}

Dabei ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} eine natürliche Zahl und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} die Resonatorlänge. Andere Frequenzen werden durch destruktive Interferenz ausgelöscht. Ein anderer Aufbau ist der Ringresonator, bei dem das Licht durch mehrfache Reflexion einen geschlossenen Pfad durchläuft.

Die Güte des Resonators (d. h. das Verhältnis zwischen hin- und herreflektierter Strahlung zu austretender Strahlung) muss bei gering verstärkenden Medien besonders hoch sein. Ein Beispiel hierfür ist der Helium-Neon-Laser. Die Resonatorgüte kann oft mittels in ihm befindlicher optischer Komponenten zeitabhängig, aber auch hinsichtlich der Wellenlänge und des lateralen Strahlprofiles beeinflusst werden, um eine gute Strahlqualität, Frequenzkonstanz und Kohärenz sowie Pulsformung des Laserstrahls zu erzielen. Solche Komponenten sind z. B. Blenden, optische Schalter (Güteschalter) oder frequenzselektive Endspiegel.

Die Resonatorstabilität kann bei einfachen Resonatoren (Spiegel – aktives Medium – Spiegel) mit den sog. g-Faktoren berechnet werden. Sie sind definiert als:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_1 = 1 - \frac{L}{R_1} }

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_2 = 1 - \frac{L}{R_2} }

Hierbei sind Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_1} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_2} die Krümmungsradien der beiden Resonatorspiegel und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} die Gesamtlänge des Resonators. Die Stabilitätsbedingung lautet

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0 < g_1g_2 < 1 }

Ein paraxialer Strahl verlässt selbst nach beliebig vielen Reflexionen den Resonator nicht. Ist das Ergebnis gerade 0 oder 1, ist der Resonator grenzstabil. Ein Beispiel hierfür ist der konfokale (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_1 = g_2 = 0} ), hemisphärische (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_1 = 0,\ g_2 = 1} ), konzentrische (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_1 = g_2 = -1} ) oder plan-plan Resonator (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_1 = g_2 = 1} ), welcher auch als Fabry-Pérot-Resonator bekannt ist. In der Praxis sind diese Art Laser sehr schwierig zu justieren und laufen meistens nur dadurch, dass andere Linseneffekte den Resonator in den Bereich der Stabilität führen. Ein solcher Effekt kann beispielsweise ein thermischer Linseneffekt sein, bei dem durch einen Temperaturgradienten im Resonator eine thermische Linse entsteht. Stabile Resonatoren beeinflussen die Strahlqualität und die Kohärenzeigenschaften des Laserstrahls positiv. Der Nachteil ist die schlechte Ausnutzung des Lasermediums, da der Lichtstrahl immer wieder auf dieselben Teilchen trifft, anstatt neue Teilchen anzuregen.

Bei instabilen Resonatoren gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_1 g_2 > 1} oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_1 g_2 < 0} . Für diese sind die Beugungsverluste sehr hoch, jedoch können durch ein Lasermedium mit großem Durchmesser instabile Resonatoren vorteilhaft genutzt werden, da diese eine gleichförmige Intensitätsverteilung im Resonator erzeugen. Voraussetzung hierfür ist jedoch eine hohe Verstärkung des Lasermediums. Instabile Resonatoren werden daher meistens in Lasern verwendet, die eine hohe Verstärkung pro Resonatorumlauf besitzen und bei denen vorrangig hohe Ausgangsleistung und weniger die Strahlqualität maßgebend sind. Von besonderer Bedeutung ist der asymmetrische konfokale instabile Resonator, da dieser einen parallelen Ausgangsstrahl liefert.

Da bei der Erzeugung von Laserstrahlung ein nicht unerheblicher Teil der aufgewendeten Energie in Wärme umgewandelt wird, ist bei der Konstruktion von Laserresonatoren, gerade im Hochleistungsbereich, auch stets auf eine effiziente Kühlung des Laseraktivenmediums zu achten. Hierbei spielen auch durch einen Temperaturgradienten im Laseraktivenmedium verursachte optische Effekte eine große Rolle, wodurch die Fokuslage innerhalb des Resonators von dessen Temperatur abhängt. Bei Gaslasern kann eine effiziente Kühlung beispielsweise dadurch erreicht werden, dass das verwendete Gas ständig umgewälzt wird, um es außerhalb des eigentlichen Lasers zu kühlen.

Longitudinale Moden

Mögliche Wellenlängen zwischen den Resonatorspiegeln. Darstellung: Amplitude als Funktion des Abstandes von den Spiegeln

Longitudinale Lasermoden bei gaußförmigem Verstärkungsprofil in einem Resonator. Darstellung: Amplitude als Funktion der Frequenz

Unterschiedliche Schwingungsformen werden Moden genannt. Als longitudinal bezeichnet man die Schwingung längs der Ausbreitungsrichtung der Strahlung. Bildlich ausgedrückt handelt es sich dabei um Intensitätsberge und -täler im Abstand einer halben Wellenlänge. Bei einem He-Ne-Laser von einigen Zentimetern Länge könnte man zwischen den Spiegeln etwa 600.000 Intensitätsberge zählen, bei einer kurzen Laserdiode nur einige Tausend.

Je nach Bauart werden vom Resonator bestimmte Wellenlängen und deren Vielfache besonders verstärkt, weil sich nur für bestimmte Wellenlängen eine stehende Welle zwischen den Spiegeln ergibt.

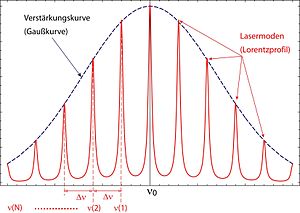
Das Bild zeigt die Intensitätsverteilung rund um die Grundmode (angegeben als mittlere Intensität in Abhängigkeit von der Frequenz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_0} ).

Für die möglichen Lichtfrequenzen in einem Laserresonator gilt der Zusammenhang:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu(N) = N \cdot \frac{c}{2L} } ,

$\nu (N)$ ist dabei die zulässige Frequenz der $N$-ten Mode, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} die Lichtgeschwindigkeit und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} die Resonatorlänge (Abstand zwischen den Resonatorspiegeln). In dieser Formel kann man die Frequenz durch den gebräuchlicheren Begriff Wellenlänge ersetzen und erhält für die möglichen Wellenlängen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda } in einem Resonator:

$2L=N\cdot \lambda$

Ein optischer Resonator wirkt also wie ein Kammfilter, das bestimmte aufeinanderfolgende Frequenzen verstärkt oder abschwächt.

Durch gaußförmige Dopplerverbreiterung der an sich scharfen Emissionslinie entsteht die gaußförmige Einhüllende über eine gewisse Anzahl von „Kammzinken“. Auf Grund obiger Resonatoreigenschaft (und der wieder anschließenden Dopplerverbreiterung) werden mehrere Teillinien der Emissionslinie des aktiven Mediums im Resonator verstärkt. Die einzelnen im Resonator verstärkten Teillinien haben ein Lorentzprofil mit sehr geringen Linienbreiten wegen der großen Länge der Wellenzüge im Resonator, und weil bei der Resonanz Störeffekte wie der Doppler-Effekt in den Hintergrund treten. Somit erhält man das nebenstehende Spektrum mit mehreren Lorentz-Kurven (den sogenannten Lasermoden) mit einer gaußförmigen Einhüllenden. Da jedoch eine Mindestintensität nötig ist, damit im Resonator noch eine Verstärkung stattfinden kann, erhält man nur eine begrenzte Anzahl Moden, da Moden, die zu weit vom Linienschwerpunkt entfernt sind, zu wenig intensiv sind, um noch verstärkt zu werden.

Der Frequenzabstand zwischen zwei benachbarten Moden ist:

$\Delta \nu ={\frac {c}{2L}}$

Nach vier Reflexionen erreicht der Lichtstrahl den Startpunkt

Es kann sich auch ein Zustand einstellen, bei dem der Strahl zweimal durch den Resonator hin- und herlaufen muss, um wieder zum Ausgangspunkt zu gelangen. Dadurch wird die effektive Resonatorlänge verdoppelt, und die Modenabstände werden auf $\Delta \nu ={\frac {c}{4L}}$ halbiert.

Die Halbwertsbreite $\Delta$ der Maxima ist

$\Delta ={\frac {\mathrm {FSR} }{\mathcal {F}}}$

Der dabei auftretende Faktor ${\mathcal {F}}$ wird als Finesse bezeichnet und ist die entscheidende Kennzahl für Resonatoren, die das spektrale Auflösungsvermögen angibt. $\mathrm {FSR}$ gibt den freien Spektralbereich des Resonators an. Die Finesse hängt bei Vernachlässigung der Verluste im Resonator nur vom Reflexionsfaktor $R$ der Spiegel ab:

${\mathcal {F}}={\frac {\pi {\sqrt {R}}}{1-R}}$

Je nach verwendeten Spiegeln kann die Finesse Werte von etwa 10 bis zu mehreren 100.000 annehmen.

In vielen Anwendungen sind mehrere longitudinale Moden unerwünscht. Eine Verkürzung der Resonatorlänge, um nur eine Mode zu erzeugen, ergibt aber meist keinen Sinn, da dadurch nicht die gewünschte Lichtleistung erzielt werden kann. Man behilft sich, indem im Resonator ein sogenanntes Etalon eingebracht wird. Das Etalon stellt im Prinzip einen „Resonator im Resonator“ dar, welcher nur Wellen der gewünschten Mode verstärkt, andere Moden aber unterdrückt. Man spricht in diesem Fall von Monomode- oder Singlemode-Lasern (im Gegensatz zu Multimode-Lasern).

Transversale Moden

Feldstärke und Intensität eines Laserstrahls in der TEM₀₀-Mode

TEM-Profile bei zylindrischen Resonatoren

Verschiedene Intensitätsprofile für einen Resonator mit rechteckigen Spiegeln (TEM_xy)

Als transversale Moden bezeichnet man die Verteilung der Phasenlage der Wellen senkrecht zur Ausbreitungsrichtung. Bildet sich also eine Mode aus, die nicht den Raum senkrecht zu den Resonatorspiegeln ausfüllt, sondern etwas schräg verläuft, so wird der Licht- und Resonatorweg länger, und die Frequenz verschiebt sich etwas. Dieses führt einerseits zum Konkurrieren um angeregte Mediumsmoleküle zwischen den verschiedenen Frequenzen (Mode Competition), andererseits können sich so stehende Wellen ausbilden, die Knotenlinien innerhalb des Laserprofils aufweisen. Ob und wie sie in einem Laserstrahl vorkommen, lässt sich durch optische Bauelemente wie Polarisationsfilter oder diffraktive optische Elemente bestimmen.

Die Art der transversalen Moden hängt von der Konstruktion des Lasers ab:

• Bei Verwendung ebener Reflektoren treten TEM-Moden auf, das heißt, in Ausbreitungsrichtung besitzt die elektromagnetische Welle keine elektrischen oder magnetischen Komponenten. Das trifft auch für die Lichtausbreitung im Freiraum zu.
• Die Mehrzahl der Laser verwendet gekrümmte Spiegel, dann treten fast immer Hybrid-Moden auf, die auch in Ausbreitungsrichtung elektrische und magnetische Komponenten besitzen.

(In Hohlleitern mit metallischer Hülle beobachtet man auch reine TE- bzw. TM-Moden, weil in der Hüllfläche elektrische Ströme fließen können.)

Bei zylindrischem Querschnitt des Lasers hat die Strahlintensität im Idealfall ein Gauß-Profil; diese Mode wird als TEM₀₀-Mode bezeichnet (siehe auch: Moden#Weitere akustische Moden). Es können aber auch andere Profile mit Winkel- und radialen Abhängigkeiten auftreten, die sich durch Laguerre-Polynome berechnen lassen. Ist diese Zylindersymmetrie durch Polarisationsfilter oder Brewster-Fenster gestört, treten rechteckige Symmetrien auf, die durch Hermitesche Polynome berechnet werden. Abhängig von der Anzahl ihrer Knotenlinien in horizontale und vertikale Richtung werden sie als TEM_xy-Mode bezeichnet. Für diese Moden ist teilweise der Lichtweg durch den Resonator bis zum Ausgangspunkt anders, das heißt, die Resonatorlänge erscheint verändert. Dies kann zu einer Verfälschung der Longitudinalmodenspektren führen, indem sich die Spektren verschiedener Transversalmoden überlagern.

Eigenschaften von Laserstrahlung

Charakteristische Eigenschaften eines Laserstrahls eines Impuls­lasers (Messungen vom PHELIX-Hochenergielaser am GSI in Darmstadt):
1. Nahfeld mit Füllfaktor und Energiedichte,
2. Strahlqualität im Fernfeld,
3. Pulsdauer und spektrale Breite (Linienbreite)

Die Strahleigenschaften eines Laserstrahles werden wesentlich durch die Art des Laser-Resonators bestimmt, insbesondere spielen dabei die Geometrie des aktiven Mediums und die Spiegelanordnung eine wichtige Rolle. Mit Lasern gelingt es, Licht in hohem Grade zu kontrollieren bzw. zu manipulieren (Brillanz, Intensität, Richtung, Frequenz, Polarisation, Phase, Zeit). Eine allgemeine Aussage über die Strahleigenschaften ist daher nicht möglich. Es ist auch nicht richtig, dass ein Laserstrahl immer ein enggebündelter Strahl mit geringer Frequenzbreite sein muss, wofür er allerdings oft gehalten wird. Je nach Zielsetzung ist eine Erzeugung derartiger Strahlen aber durchaus möglich. Eine herausragende, allgemeine Eigenschaft stellt jedoch die Möglichkeit zur starken Bündelung dar, mit der sehr hohe Leistungsdichten erzielt werden können. Die laterale Leistungsdichteverteilung von Laserstrahlen ist bei guter Strahlqualität ein Gaußprofil (Gauß-Strahl).

Generell kann man zu den Strahleigenschaften sagen, dass Laserstrahlen sich gegenüber gewöhnlichen Lichtquellen durch viele Unterschiede auszeichnen, die im Folgenden genannt werden.

Kohärenz

→ Hauptartikel: Kohärenz

Bei einer normalen Glühlampe werden Lichtwellen nicht nur mit unterschiedlicher Wellenlänge ausgesendet, sondern auch in unbestimmter Phasenlage zueinander. Bei einem Laser dagegen sind die Wellen über mehr oder weniger lange Strecken (Kohärenzlänge) phasengleich, was man sich zum Beispiel in der Holografie zunutze macht.

Polarisation

→ Hauptartikel: Polarisation

Die Polarisation von Laserstrahlen ist aufgrund polarisierender optischer Bauteile im Resonator (schräge Umlenkspiegel und Brewster-Fenster, geringe Höhe des Resonators bei Halbleiterlasern) meistens linear. Oft ist das erwünscht, um polarisationsabhängige Kopplung und Strahlteilung durchführen zu können. Beim Schneiden von Metallen tritt jedoch insbesondere bei der linear polarisierten CO₂-Laserstrahlung im Schneidspalt eine polarisationsabhängige Absorption auf, was eine schlechte und richtungsabhängige Schnittkantenqualität zur Folge hat. Daher wird beim Metallschneiden mit zirkularer Polarisation gearbeitet, die durch phasendrehende Verzögerungsplatten im Strahlengang des Laserstrahls erzielt wird.

Frequenz, Wellenlänge

Die Frequenz von Laserstrahlung wird durch das aktive Medium und dessen zum Lasern geeignete Energieübergänge bestimmt. Es gibt Stoffe, die auf vielen Wellenlängen zum Lasern angeregt werden können – jedoch meistens bei einer Wellenlänge besonders gut. Laser können sehr schmalbandige Strahlquellen sein, die Verstärkungsbandbreite (beim Kohlenstoffdioxidlaser zum Beispiel 9 bis 11 µm) ist jedoch meist höher als die Bandbreite der abgegebenen Strahlung – entweder schwingt der Laser von selbst im Maximum der Verstärkungsbandbreite (beim Kohlendioxidlaser zum Beispiel 10,6 µm) an oder man sorgt durch frequenzbestimmende Elemente für eine schmalbandige Emission auf einer einzigen Frequenz. Extreme Schmalbandigkeit ist z. B. bei der interferometrischen Längenmessung mittels Lasern von Bedeutung. Bei extremer Breitbandigkeit spricht man von Superkontinuum-Lasern, welche z. B. in der optischen Kohärenztomographie und zur Erzeugung von Frequenzkämmen eingesetzt werden. Die minimal erreichbare Bandbreite wird durch die fundamentale Laser-Linienbreite beschrieben. Das Schawlow-Townes-Limit ist eine vierfache Näherung dieser fundamentalen Laser-Linienbreite.

Lasertypen nach der Signalform

Dauerstrich

Ein Dauerstrichlaser ist ein Laser, der im Gegensatz zu Pulslasern eine Lichtwelle konstanter Intensität abstrahlt.

Laserstrahlung von Dauerstrichlasern (englisch continuous-wave laser, cw-laser) ist im Idealfall schmalbandig (monochrom, einfarbig), d. h., sie besteht nur aus Strahlung einer Wellenlänge. Insbesondere ist Dauerstrich-Laserstrahlung aus stabilen Laserresonatoren aufgrund des Vielfachumlaufes zeitlich bzw. longitudinal (entlang seiner Ausbreitungsrichtung) kohärent, was bedeutet, dass die ausgesandten Wellenzüge nicht nur mit der gleichen Frequenz schwingen, sondern auch in der Phase über eine lange Strecke (die Kohärenzlänge) konstant sind. Dadurch zeigt ein solches Licht besonders ausgeprägte Interferenzerscheinungen.

Während des Einschwingvorgangs des Dauerstrich-Lasers tritt zunächst oft Spiking auf, eine unregelmäßige Abgabe von Laserpulsen. Dieses Verhalten nutzt ein modengekoppelter Laser gezielt aus, indem er die Spikes z. B. triggert oder synchronisiert.

Pulse

→ Hauptartikel: Pulslaser

Im Gegensatz zum Dauerstrichlaser erzeugt ein gepulster Laser pulsierende Strahlung. Pulse können durch gepulste Anregung oder auch durch Maßnahmen im Laser selbst (Güteschaltung) erzeugt werden. Bei sehr kurzen Pulsen benötigt das aktive Medium prinzipiell eine größere Verstärkungsbandbreite, innerhalb derer die beteiligten Frequenzen gekoppelt sind (Modenkopplung) und sich zu einem Impuls zusammensetzen. Je kürzer die Pulsdauer, desto breiter ist entsprechend den Gesetzen der Fourier-Analyse das erzeugte Spektrum und umso breiter muss das Frequenzband sein, innerhalb dessen das aktive Medium verstärken kann. Die geringsten erzielbaren Pulsdauern liegen in der Größenordnung von Femto- und Attosekunden (→ Femtosekundenlaser).

Laser können sich auch selbst zur Abgabe einer Pulsfolge synchronisieren, wenn im Resonator zum Beispiel ein nichtlinearer (sättigbarer) Absorber vorhanden ist. Die Wiederholfrequenz, mit der die Pulse in einem solchen Laser erzeugt werden, hängt u. a. bei der instantanen Kerr-Linsen-Modenkopplung (englisch Kerr lens mode locking, ein Verfahren zur Erzeugung einer stabilen Pulsfolge von Pulsen geringer Dauer) von der Resonatorlänge ab: Bei einem Resonator mit einer Länge von einem halben Meter beträgt diese etwa 300 MHz – die Periodendauer entspricht einem Hin- und Herlaufen (Umlauf) des Pulses im Resonator. Die Spitzenleistung wird bei jedem Umlauf größer, die Pulsdauer bleibt von allein sehr gering. Aus solchen Pulslasern werden zum Beispiel einzelne Pulse mittels optischer Schalter herausgelassen und weiterverstärkt. Mit weiteren Maßnahmen gelingt es, Spitzenleistungen bis in den Petawatt-Bereich zu erzeugen, die nur im Vakuum ungestört übertragen und fokussiert werden können. Luft wird von der hohen elektrischen Feldstärke des Lichts ionisiert.

Die Gütemodulation (Q-switching) des Resonators mit akustooptischen Güteschaltern oder Pockelszellen sind weitere Techniken zur Erzeugung energiereicher Laserpulse mit geringer Dauer: Dabei wird die stimulierte Emission zunächst unterbunden, um sie dann bei inzwischen durch das Pumpen gestiegener Besetzungsinversion (hohe, im aktiven Medium gespeicherte Energie) schlagartig zu ermöglichen.

Einteilung anhand des Lasermediums

→ Hauptartikel: Liste der Lasertypen

Grobe Einteilung von Lasertypen

Laser                                                                                   Gas                 Farbstoff                                                                 Ionen   Metalldampf   neutrales Nichtmetall                                                                       Festkörper                                                                                   Halbleiter   Farbzentrum   Dotierte Nichtleiter

Datei:Commercial laser lines.de.svg

Übersicht über Wellenlängen von im Handel erhältlichen Lasern. Lasertypen mit diskreten Laserlinien sind oberhalb der Leiste der Wellenlängen eingetragen. Die Farbe gibt die Art des Lasermaterials an.

Laser werden oftmals anhand der Eigenschaften des eingesetzten optischen Lasermediums kategorisiert und benannt. Die gröbste Einteilung erfolgt dabei anhand des Aggregatzustandes.

Wichtige Gaslaser sind beispielsweise der bei 632,8 nm emittierende Helium-Neon-Laser und der bei 10,6 μm emittierende Kohlendioxidlaser. Spezielle Klassen der Gaslaser sind Excimerlaser, bei denen das Lasermedium ein Excimer-Molekül ist, und Metalldampflaser, bei denen das gasförmige Lasermedium zuerst durch Verdampfen von Metall gewonnen werden muss.

Laser mit flüssigem Lasermedium werden als Farbstofflaser bezeichnet. Diese Laser kennzeichnen sich durch eine sehr große, kontinuierliche und abstimmbare Bandbreite an Wellenlängen. Bei den eingesetzten Farbstoffen handelt es sich in vielen Fällen um Stilbene, Cumarine und Rhodamine.

Die Gruppe der Festkörperlaser beinhaltet Laser, deren Lasermedium Kristalle sind. Dabei kann es sich unter anderem um dotiertes Glas, Yttrium-Aluminium-Granat und andere Wirtskristalle oder Halbleiter handeln. Wichtige Beispiele sind der Nd:YAG-Laser, die Laserdiode und der Titan:Saphir-Laser. Häufig verwendete Dotanden sind Titan, Chrom und Neodym. Für die Form der Festkörper existieren viele Möglichkeiten, wie z. B. der Stablaser, Slablaser, Faserlaser und der Scheibenlaser. Eine besondere Form der Festkörperlaser sind die Farbzentrenlaser, die ähnlich funktionieren, aber Farbzentren zur Erzeugung der Laserübergänge nutzen.

Eine besondere Form ist der Freie-Elektronen-Laser (FEL). Er ist eine Synchrotronstrahlungsquelle, die gerichtete Strahlung im Mikrowellenbereich bis in den Röntgenbereich emittiert. Ein FEL ist allerdings kein Laser im eigentlichen Sinne, da die Strahlung nicht durch stimulierte Emission in einem Lasermedium erzeugt wird.

Anwendungen

[[Hilfe:Cache|Fehler beim Thumbnail-Erstellen]]:

Eine Laserharfe

Datei:Lasergravur.jpg

Laserbeschriftetes Schaltkreis-Gehäuse aus Keramik; Zeichenhöhe ca. 1,34 mm

[[Hilfe:Cache|Fehler beim Thumbnail-Erstellen]]:

Laser am Paranal-Observatorium

Laser werden in sehr vielen Lebens- und Arbeitsbereichen, Forschungs- und Industriezweigen und medizinischen Aufgabenfeldern verwendet. Folgende Abschnitte geben einen groben Überblick über die wichtigsten Einsatzgebiete der Lasertechnik.

Alltag und Unterhaltung

Laser haben Einzug in vielen Bereichen des täglichen Lebens gefunden. In jedem Laserdrucker und allen optischen Laufwerken, wie beispielsweise CD-, DVD- und Blu-ray-Disc-Spieler, befinden sich Laserdioden.

Laserpointer enthalten schwache Laser mit sichtbaren Wellenlängen. In Diskotheken und Lasershows werden Laser mit bis zu mehreren Watt Ausgangsleistung zu Lichteffekten eingesetzt. Bei der sogenannten Laserharfe wird ein aufgefächerter Laserstrahl als Eingabegerät zum Ansteuern von Musikinstrumenten benutzt. In Planetarien werden Laser vereinzelt als Projektoren eingesetzt. Eine Variante ist der „All Dome Laser Image Projector“, wie er zum Beispiel im Planetarium Jena verwendet wird. In Barcodelesegeräten werden teilweise Laser zum Abtasten der Strichcodes verwendet.

Datengewinnung und -übertragung

Ein bedeutendes Einsatzgebiet von Diodenlasern und Faserlasern ist die Datenübertragung mittels Lichtwellenleitern. Der optische Richtfunk ist zwar möglich, aber wegen der Störanfälligkeit wenig verbreitet. Die Datenübertragung zwischen Satelliten oder Raumfahrzeugen mittels Laser ermöglicht aufgrund der höheren Frequenz eine weit höhere Datenrate als die bisher üblichen Radiowellen. Insbesondere als Relais wurde die Technik bisher eingesetzt, beispielsweise von Artemis. Die Kommunikation zur Erde mit Laser ist durch die Atmosphäre behindert. Die zugehörige Technologie befindet sich noch in der Erprobungsphase, könnte aber in Zukunft eine größere Rolle spielen.

Weitere Anwendungen sind die Holografie und das Laserscanning zur Objektvermessung oder in Nivelliergeräten.

Industrie und Materialbearbeitung

In der Industrie und der Fertigungstechnik werden Laser für verschiedene Fertigungsverfahren (DIN 8580) eingesetzt. Sie werden hierzu an einer Laserbearbeitungsmaschine oder einem Laserscanner betrieben. Laser eignen sich zum Umformen, Trennen, Fügen, Beschichten und Ändern von Stoffeigenschaften verschiedener Materialien, wie Holz, Kunststoff, Papier und Metallen.

Zu den wichtigsten Verfahren gehören das Lasersintern, die Stereolithografie, das Laserstrahlbiegen und laserunterstützte Biegen, das Laserschneiden und -bohren, die Laserablation, das Lasertrimmen, Laserstrahlschweißen, -auftragschweißen und -löten, die Laserbeschriftung, das Laserspritzen und Laserstrahlverdampfen, das Laserpolieren.

Weiterhin können mit Lasern Strukturen im Mikrometer- und Submikrometerbereich auf fotosensitive Materialien geschrieben werden. Mittels mikrofotolithografischer Systeme werden im Direktschreibverfahren hochaufgelöste Vorlagen (Masken) für verschiedene Anwendungen erzeugt, die z. B. mittels breitbandiger Hochleistungslaser in der Produktion auf die endgültigen Materialien umkopiert werden. Andere Anwendungen schließen das Direktschreiben von Strukturen auf Silizium-Wafern in niedrigen Stückzahlen oder das Schreiben von Strukturen auf fotoempfindlichen Filmen (z. B. Dehnungssensoren) ein. Auf diese Weise lassen sich Bildschirmmasken, Leiterplatten, integrierte Schaltkreise und Sensoren herstellen.

Medizin

In der Allgemeinmedizin wird der Laser hauptsächlich in der Diagnose eingesetzt, z. B. bei der Messung von Blutstrom (Flowmetrie) und -zirkulation. Es existieren auch Low-Level-Lasertherapiegeräte zur Wund- und Schmerzbehandlung.

In der Augenheilkunde wird Laserlicht mit unterschiedlichen Wellenlängen eingesetzt, wobei Wellenlänge, Einwirkzeit (Expositionszeit) und Energie die physikalische Reaktion und Eindringtiefe beeinflussen. Der Argon-Laser wird genutzt, um mit seinen thermischen Effekten Koagulation (z. B. bei diabetischer Retinopathie, Thrombosen) deren Gefäßneubildungen zu verhindern oder Retinopexie (Verschweißung von Gewebeschichten bei Netzhautloch oder Netzhautablösung) durchzuführen. Der Neodym-YAG Laser und femto-LASER verursacht durch den hervorgerufenen hochenergetischen ultrakurzen Suprapuls eine präzise eng umschriebene Gewebezerreißung (Photodisruption) und der Excimer-Laser durch das ihm eigene Phänomen der Gewebeverdunstung (Photoablation/Sublimation) eine Umgestaltung der Hornhaut-Oberfläche (z. B. PRK oder LASIK) zur Beseitigung der Fehlsichtigkeit. Die Femtosekundenlaser-Kataraktoperation ist eine neue Methode in der Chirurgie des Grauen Stars (Katarakt), die bei einigen wichtigen Schritten während dieses Eingriffs von besonders hoher Präzision ist. Darüber hinaus sind mit dem Laser dreidimensionale bildgebende Verfahren möglich wie optische Coherenz-Tomographie (OCT) oder online-Pachymetrie, optische Pfadmessung und Fotodokumentation aller Augenstrukturen mit einer Auflösung im Mikrometerbereich.

In der Chirurgie, Gefäßchirurgie und Phlebologie wird der Laser hauptsächlich im Bereich Endoskopie oder als Laserskalpell eingesetzt. Eine weitere Anwendung ist die Behandlung von defekten Venen (Krampfadern). Hierbei kann der Laser endovenös (Laser-Lichtleiter wird in die Vene eingebracht) angewendet werden. Dieses Laser-Behandlungsverfahren ersetzt dabei das Entfernen der Vene durch „Stripping“. Die Laser-Behandlung ist in vielen Fällen schonender und ambulant durchführbar.

In der Dermatologie lassen sich mit Laserstrahlen Schnitte und Verödungen durchführen. Blutgefäße können durch Laser bestimmter Wellenlängen koaguliert werden. Pigmentflecken können mit Hilfe ablatierender (= schälender) Laser abgetragen oder selektiv zerstört werden. Subkutanes (= unter der Haut gelegenes) Pigment kann mit Hilfe eines ultrakurz gepulsten Lasers zerstört und damit entfernt werden, ohne die Hautoberfläche stark zu verletzen. Durch Verwendung von langgepulsten Lasern können Haarwurzeln durch Epilation dauerhaft zerstört werden. Laser werden auch zur gezielten Behandlung entzündlicher Hauterkrankungen, vorrangig der Psoriasis (Schuppenflechte), eingesetzt. Oberflächliche Unebenheiten der Haut (Knötchen, Fältchen) werden mit zur kosmetischen Verbesserung des Hautbildes geglättet (Resurfacing). Durch Laserlicht können auch selektiv dermale Anteile erwärmt werden, was in erster Linie dem Kollagenaufbau zur Straffung der Haut dienen soll („Subsurfacing“).

In der Hals-Nasen-Ohren-Heilkunde werden Laser zur Abtragung von Veränderungen an den Stimmbändern bei der Mikrolaryngoskopie verwendet, außerdem zur Teilabtragung der Mandeln (Tonsillotomie) und von Tumoren in Mund und Rachen (z. B. beim Zungenkarzinom). Bei der Operation wegen Otosklerose werden Laser zur Perforation der Steigbügel-Fußplatte verwendet.

In der Zahnmedizin können Laser für den Abtrag von Zahnhartsubstanz („Bohren ohne Bohrer“) oder in der Parodontologie (Keimreduktion und Konkremententfernung in entzündeten Zahnfleischtaschen) verwendet werden. Diodenlaser werden in der Zahnmedizin für chirurgische Eingriffe, z. B. Lippenbändchenentfernung, für die Keimreduktion in der Endodontie (Wurzelkanalbehandlung) oder für die Zahnaufhellung (Bleaching) verwendet. Vorteile der Laserbehandlung gegenüber der konventionellen Methode sind, dass der Patient weniger Schmerzen hat, die Setzung von Nähten teilweise überflüssig wird, es weniger blutet, da die Wunde verödet ist und die behandelte Stelle gleichzeitig dekontaminiert (keimfrei) wird. Zum Teil sind allerdings bessere Studien mit einem höheren Evidenzgrad erforderlich, um den Nutzen des Lasers einzuschätzen.

In der Krebstherapie wird er für die photodynamische Therapie eingesetzt; in der Urologie zur Behandlung von Nieren- und Harnleitersteinen und der Prostata. Die Lasermikrodissektion ist ein Verfahren zur Gewinnung von kleinsten Proben aus Gewebsschnitten oder Zellkulturen.

Noch in der Forschung befindliche Techniken betreffen u. a. die Versuche, Nerven unter Einsatz von Laserlicht zielgerichtet wachsen zu lassen.

Die Sicherheitsbestimmungen für medizinisch genutzte Laser werden in der EN 60601-2-22 behandelt.

Mess- und Steuerungstechnik

Eine Reihe von präzisen Messgeräten für Entfernungen und andere Größen funktionieren mit Lasern. Sie werden beispielsweise beim Tunnelbau, im Bauwesen und zur Vermessung der Maschinengeometrie bei Werkzeugmaschinen und Anlagen verwendet.

Weitere Messgeräte, die auf Lasern beruhen, sind Kohärenzradar, optische Abstandsmessungen per Light detection and ranging (Lidar) und Laserpistolen, lasergestützte Brandmelder, elektronische Specklemuster-Interferometrie (ESPI) zur Formerfassung, Lasermikrofone, Laserextensometer, Laser-Doppler-Anemometrie und Particle Image Velocimetry zur Messung von Strömungsgeschwindigkeiten, Laser-Doppler-Vibrometer zur berührungsfreien Schwingungsmessung, Laser surface velocimeter, Laser-Wolkenhöhenmesser in der Meteorologie und Laserkreisel.

Energietechnik

Laser können zur Uran-Anreicherung zwecks Gewinnung von Kernbrennstoff verwendet werden.

Militär

Beim Militär und in der Rüstungsindustrie werden Laser wie im Alltag zur Kommunikation und zu Messzwecken eingesetzt, aber zusätzlich auch als Waffen oder waffenunterstützende Technik verwendet. Dazu zählen Zielhilfen für lasergelenkte Bomben und Raketen sowie zur Erzeugung von Zielmarkierungen an Handfeuerwaffen (beispielsweise an der AM180), „Lasergewehre“ zum vorübergehenden Blenden und Hochenergielaser zur Raketenabwehr (Laserkanonen) (siehe auch Energiewaffe und Weltraumwaffe).

Hochleistungs-Laseranlagen im Wellenlängenbereich um 1 Mikrometer dienen als „Treiber“ in Anlagen zur Trägheitsfusion wie beispielsweise der National Ignition Facility.

2014 wurde von der US Navy die erste Laserwaffe (englisch Laser Weapon System, kurz LaWS) auf der USS Ponce in Betrieb genommen. In veröffentlichten Videos wird die Waffe an unbemannten Flugobjekten und Schlauchbooten getestet, die nach kurzer Zeit anfangen zu brennen. 2018 wurde die russische Laserwaffe Pereswet in Dienst gestellt, die Drohnen, Flugzeuge und Raketen bekämpfen soll.

Wissenschaft und Forschung

In der Forschung der Physik, Chemie und Biologie und ihrer jeweiligen Teilgebiete sind Laser ein wichtiges Hilfsmittel. In der Laserspektroskopie werden Laser zur Laserkühlung und Bestimmung von Energieniveaus in Atomen und Molekülen, zur Dichtemessung in Gasen und Plasmen oder zur Bestimmung von Materialeigenschaften eingesetzt. Spezielle laserspektroskopische Verfahren sind beispielsweise die Atomspektroskopie, die Tunable Diode Laser Absorption Spectroscopy die Raman-Spektroskopie und die nichtlineare Raman-Spektroskopie. Effekte, wie sie die nichtlineare Optik vorhersagt, können nur mit Lasern erzielt werden. Isotopentrennungen, wie AVLIS und MLIS, sind ebenfalls nur mit Lasern möglich.

In der Geodäsie dienen Laser zur Vermessung der Erde und der Plattentektonik, beispielsweise mittels Tachymeter, Lasertracker, Kanallaser, Satellite Laser Ranging und LaserDisto.

Die optische Pinzette und das Zwei-Photonen-Mikroskop sind Anwendungen der Zellforschung.

In der Astronomie werden Laser zur genauen Justierung optischer Bauteile und Instrumente sowie zur Beobachtung von Raumobjekten eingesetzt. Dazu zählen Laserteleskope, Laser-Theodoliten und -Zielfernrohre sowie die Vermessung der Mondbewegung mittels Lunar Laser Ranging.

In der superauflösenden Mikroskopie mit dem STED-Mikroskop, für die Stefan Hell im Jahr 2014 (mit anderen) den Nobelpreis für Chemie erhielt, werden zwei konfokale Laserstrahlen eingesetzt, um Bereiche von nur wenigen Atom-Durchmessern abrastern zu können.

Homogenisierung

In manchen Anwendungen ist ein räumlich homogenes Profil nötig. Der Laserstrahl kann dann homogenisiert werden, zum Zwecke der Schaffung einer möglichst ebenmäßigen Intensitätsverteilung der Laserstrahlung über den gesamten Bearbeitungsfleck. Ein anfänglich zum Beispiel vorliegendes Gauß-Profil der Intensitätsverteilung soll dabei in ein fast-Rechteckprofil mit möglichst geringer Inhomogenität überführt werden. Häufiger möchte man jedoch unregelmäßige und instabile Strahlprofile homogenisieren. Das Ziel ist die gleichmäßige Ausleuchtung einer Fläche zum Beispiel zur Wärmebehandlung. Hauptmethode ist die Mehrfachreflexion in innen reflektierenden Rohren oder Lichtleitern.

Gefahren

Gefahren für die Gesundheit

Warnzeichen vor Laserstrahlen nach DIN EN ISO 7010

Laser können aufgrund der Eigenschaften ihrer Strahlung und aufgrund ihrer z. T. extrem konzentrierten elektromagnetischen Leistung biologische Schäden verursachen. Daher sind Laser je nach Laserklasse nur in eingeschränkten Räumen oder durch eingeschränktes Personal zu betreiben. Es existieren Grenzwerte der Exposition durch Laserstrahlung, abhängig von ihrer Bündelung. Dabei werden Bereiche der Wellenlängen und Einwirkzeiten unterschieden, die zu charakteristischen Verletzungen durch thermische oder photochemische Prozesse in verschiedenen Komponenten des Auges sowie auf und unter der Haut führen.

Anwender und Anlagenbauer müssen direkte, indirekte (unbeabsichtigt gerichtet reflektierte) und Streustrahlung (unbeabsichtigt diffus reflektierte) hinsichtlich der Grenzwerte berücksichtigen.

Mögliche Schäden:

• Bei der medizinischen Anwendung von Lasern kann es zur Entzündung vorhandener oder gebildeter Gase kommen.
• Laser im Ultraviolettbereich verursachen auch fotochemische Veränderungen des Gewebes. Dazu gehören Erscheinungen ähnlich einem Sonnenbrand mit dem Risiko einer Krebsentstehung sowie Trübungen der Hornhaut, der Augenlinse und des Glaskörpers.
• Bei der Lasermaterialbearbeitung entstehen durch Pyrolyse und Verdampfung meistens giftige Gase, Stäube und Aerosole, die abgesaugt und gefiltert werden müssen.
• Laserstrahlen im Nahinfrarot-Bereich (um 1000 nm) oder deren Streustrahlung dringen tief unter die Haut vor und können im Unterhautgewebe schmerzlose, schlecht heilende Verbrennungen verursachen.
• Verbrennungen im Auge: Bereits bei sehr geringen Leistungen (wenige Milliwatt) einer Wellenlänge, für die das Auge transparent ist (etwa 350 bis 1200 nm) treten im ungeschützten Auge partielle Erblindungen durch Netzhautschäden auf, da der parallele Laserstrahl durch die Augenlinse auf der Netzhaut fokussiert wird. Auch Streustrahlung stärkerer Laser dieses Wellenlängenbereiches ist gefährlich. Schäden werden oft nicht bemerkt, sondern erst vom Augenarzt entdeckt.
• Verbrennung von Auge und Haut: Treffen Laserstrahlen oder deren Streustrahlung einer Wellenlänge, für die Haut und Hornhaut nicht transparent sind (ab etwa >1400 nm), auf, kommt es bei entsprechender Leistungsdichte zu oberflächlichen Verbrennungen oder Verkohlungen.
• Ultrakurzpulslaser erzeugen beim Auftreffen auf Material bzw. im Fokus je nach Energie und Pulsdauer Röntgenstrahlung, die bei Exposition Gewebeschäden, Erbschäden oder Krebs auslösen kann.

Die Gefährdung durch Laserstrahlung an Maschinen zur Lasermaterialbearbeitung wird oft nach der Maschinenrichtlinie beurteilt und ergibt auf dem Risikograph meistens die bisherige Kategorie 4 beziehungsweise die Sicherheitsanforderungsstufe 3 (auch Sicherheits-Integritätslevel 3, kurz SIL-3). Das ist dadurch begründet, dass in der Regel irreversible Schäden der Gesundheit zu befürchten sind.

Sachschäden

Laserstrahlen können bei ausreichender Leistung oder Fokussierung Brände und Explosionen auslösen. Hochbrillante Laser zur Materialbearbeitung können bei Versagen der Steuerung (zum Beispiel eines Roboters) auch an weit außerhalb ihrer Fokusebene liegenden Bauteilen oder Wandungen Schäden verursachen.

Gefahren-Prävention

Jede Einrichtung in Deutschland, die Laser ab der Klasse 3R benutzt, muss eine unterwiesene Person, einen Laserschutzbeauftragten, benennen, der/die die Gefahren und die sichere Verwendung von Lasern kennt und überwacht.

Dabei gilt es, wenn immer möglich, die Laserstrahlung so wirksam und sicher abzuschirmen, dass die Gefährdung ausgeschlossen ist (Maschinenrichtlinie). Auch Lichtgitter können zur Absperrung angewendet werden, wenn die Streustrahlung ausreichend gering ist. Ist das nicht möglich oder angeraten (zum Beispiel bei Showlasern, im Laborbetrieb oder in medizinischen Anwendungen), muss durch Qualifikation des Personals, technische Maßnahmen und durch Schutzbrillen die Gefährdung auf ein Mindestmaß gesenkt werden. So dürfen Showlaser nie, auch bei Versagen der Steuerung oder der Spiegelablenkung, ins Publikum strahlen können.

Die vollständige Abschirmung der Strahlung der Laser mittels einer Umhausung der Maschine oder des Experimentes ist oft nicht möglich. Zugangstüren müssen dann elektrisch überwacht werden und Warnlampen müssen leuchten, solange der Laser gefährliche Strahlung abgeben kann.

Beobachtungsfenster und Schutzbrillen erlauben bei geringer Streustrahlung oft eine Beobachtung, während der Laser eingeschaltet ist, und bestehen aus Filtermaterialien, die für sichtbare Wellenlängen zumindest teilweise transparent, für die spezielle Laserwellenlänge jedoch intransparent sind.

Laserklassen

Lasergeräte werden entsprechend der schädlichen biologischen Wirkung von Laserstrahlung in Klassen eingeteilt. Maßgeblich für die nationalen und internationalen Laserklassen ist dabei die Definition von Grenzwerten, bei denen keine Schädigung zu erwarten ist. Neben der amerikanischen ANSI-Norm gibt die International Commission on Non-Ionizing Radiation Protection Grenzwerte im Spektralbereich zwischen 400 und 1400 nm heraus.

Maßgeblich ist bei nichtionisierender Strahlung die thermische Leistung pro Fläche sowie die spezifischen wellenlängenabhängigen Absorptionseigenschaften des Gewebes (Haut sowie Retina, Hornhaut, Glaskörper und Linse des Auges). Durch die Fokussierung der Augenlinse ist die Gefährlichkeit im sichtbaren und besonders im angrenzenden infraroten Bereich erhöht.

Oberhalb von 1,4 µm Wellenlänge wird die Strahlung großflächig in der Hornhaut absorbiert. Sie bietet einen Schutz für die Retina des Auges. Jedoch reduziert sich die Absorptionstiefe auf weniger als 0,1 mm bei 3 µm Wellenlänge, weshalb es zu Schäden in der Hornhaut kommen kann. Aus diesem Grund heißt der Wellenlängenbereich von 1,5 bis 2 µm augensicher (englisch eye safe).

Unterhalb 1,4 µm sind Hornhaut, Haut und darunter liegendes Gewebe im Bereich 1200 nm (Nahinfrarot) bis rot (700 nm) teiltransparent, sodass hier tiefreichende Schädigungen auftreten können, deren Entstehung aufgrund dort nicht vorhandenen Wärmeempfindens oft nicht bemerkt werden. Auch Netzhautschäden durch Laser-Strahlung im Nahinfrarot werden oft nicht bemerkt und erst durch für entsprechende Arbeitsplätze vorgesehene ärztliche Augenuntersuchungen entdeckt.

Bei Wellenlängen unterhalb von etwa 400 nm werden organische Molekülbindungen zerstört, die Absorptionstiefe im Gewebe verlagert sich mit kürzerer Wellenlänge an die Oberfläche von Haut und Auge. Es treten auch bei geringen thermischen Leistungsdichten Linsen- und Hornhauttrübungen sowie Schädigungen der Haut vergleichbar einem Sonnenbrand auf. Dementsprechend sind die Grenzwerte der Leistungsdichte bei diesen kurzen Wellenlängen geringer als beispielsweise im mittleren Infrarot.

Die Klasseneinteilung von Lasergeräten und -anlagen erfolgt anhand maximal auftretender Leistungs- bzw. Energiedichten, je nachdem, ob es sich um kontinuierliche oder Pulslaser handelt. Dabei ist auch die Expositionsdauer und die Wellenlänge maßgebend.

Klassifizierung nach DIN EN 60825-1

[[Hilfe:Cache|Fehler beim Thumbnail-Erstellen]]:

Maximale cw-Leistungen für Laser der Klassen 1, 2, 3R und 3B gemäß EN 60825-1:2007.
Die angegebenen Leistungen gelten nur für punktförmige Quellen und stark kollimierte Laserstrahlung. Bei ausgedehnten Quellen und divergenter Strahlung sind höhere Leistungen zulässig.

Ein nach EN 60825-1 gekennzeichteter Laser, es fehlt jedoch eine Warnlampe

Entsprechend der Gefährlichkeit für den Menschen sind die Laser in Geräteklassen eingeteilt. Die Klassifizierung nach DIN EN 60825-1 erfolgt vom Hersteller. (Die alte Klassifizierung nach DIN VDE 0837 (→ unten) darf für neue Laser nicht mehr verwendet werden.)

Klasse	Beschreibung
1	Die zugängliche Laserstrahlung ist ungefährlich, oder der Laser befindet sich in einem geschlossenen Gehäuse
1C	Die zugängliche Laserstrahlung ist ungefährlich für das Auge, aber in besonderen Fällen gefährlich für die Haut.
1M	Die zugängliche Laserstrahlung ist ungefährlich, solange keine optischen Instrumente wie Lupen oder Ferngläser verwendet werden.
2	Die zugängliche Laserstrahlung liegt nur im sichtbaren Spektralbereich (400 nm bis 700 nm). Sie ist bei kurzzeitiger Bestrahlungsdauer (bis 0,25 s) auch für das Auge ungefährlich.
2M	Wie Klasse 2, solange keine optischen Instrumente wie Lupen oder Ferngläser verwendet werden.
3R	Die zugängliche Laserstrahlung ist gefährlich für das Auge.
3B	Die zugängliche Laserstrahlung ist gefährlich für das Auge und in besonderen Fällen auch für die Haut. Diffuses Streulicht ist in der Regel ungefährlich. (Laser von CD-/DVD-Brennern; Laserstrahlung allerdings nicht direkt zugänglich)
4	Die zugängliche Laserstrahlung ist sehr gefährlich für das Auge und gefährlich für die Haut. Auch diffus gestreute Strahlung kann gefährlich sein. Beim Einsatz dieser Laserstrahlung besteht Brand- oder Explosionsgefahr. (Materialbearbeitung, Forschungslaser)

Anmerkung zu Laserklasse 2 und 2M: Eine wissenschaftliche Untersuchung ergab, dass der Lidschlussreflex (dieser tritt innerhalb 0,25 s auf; eine längere Bestrahlung schädigt das Auge) nur bei ca. 20 % der Testpersonen gegeben war. Vom Vorhandensein des Lidschlussreflexes kann daher nicht als Regelfall ausgegangen werden.

Anmerkung zur Leistung: Bei Lasern, die ausgedehnte Lichtquellen darstellen und/oder divergente Strahlung abgeben, können weit höhere Leistungen zulässig sein als bei kollimierten Lasern derselben Klasse. So wird z. B. auf Seite 67 von EN 60825-1:2007 das Beispiel B.3.2 angegeben, bei dem eine stark divergente 12-mW-Laserdiode (Wellenlänge 900 nm) nach Klasse 1M klassifiziert wird.

Klassifizierung nach DIN VDE 0837

Bis März 1997 galten in Deutschland die Laserklassen nach DIN VDE 0837. Diese Einteilung ist heute noch in den USA gebräuchlich.

Klasse	Beschreibung
1	entspricht der Klasse 1 nach EN 60825-1
2	entspricht der Klasse 2 nach EN 60825-1 Laser dieser Klasse werden unter Umständen heute in 1M eingestuft.
3a	Die zugängliche Laserstrahlung wird für das Auge gefährlich, wenn der Strahlquerschnitt durch optische Instrumente verkleinert wird. Ist dieses nicht der Fall, ist die ausgesandte Laserstrahlung im sichtbaren Spektralbereich (400 nm bis 700 nm) bei kurzzeitiger Bestrahlungsdauer (bis 0,25 s), in den anderen Spektralbereichen auch bei Langzeitbestrahlung, ungefährlich. Je nach Wellenlänge werden diese Laser heute meistens in Klasse 2M oder 3R eingestuft.
3b	entspricht der Klasse 3B nach EN 60825-1
4	entspricht der Klasse 4 nach EN 60825-1

Literatur

• Fritz Kurt Kneubühl, Markus Werner Sigrist: Laser. 7. Auflage. Teubner, Wiesbaden 2008, ISBN 3-8351-0145-5.
• Jürgen Eichler, Hans Joachim Eichler: Laser. Bauformen, Strahlführung, Anwendungen. 7. Auflage. Berlin/Heidelberg, Springer 2010, ISBN 3-642-10461-4.
• Jeff Hecht: Beam: The Race to Make the Laser, Oxford UP 2005
• Anthony E. Siegman: Lasers. University Science Books, Mill Valley, CA 1986, ISBN 0-935702-11-3.
• William T. Silfvast: Laser Fundamentals. 2. Auflage. Cambridge University Press, Cambridge 2004, ISBN 0-521-83345-0.
• Axel Donges: Physikalische Grundlagen der Lasertechnik. Shaker, Aachen 2007, ISBN 978-3-8322-6392-8.
• Charles H. Townes: How the Laser Happened. Oxford University Press, New York/Oxford 1999, ISBN 0-19-512268-2.
• Ute Mauch: Lasermedizin. In: Werner E. Gerabek, Bernhard D. Haage, Gundolf Keil, Wolfgang Wegner (Hrsg.): Enzyklopädie Medizingeschichte. De Gruyter, Berlin / New York 2005, ISBN 3-11-015714-4, S. 827 f.

Weblinks

Commons

Commons: Laser – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Laser – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Laser in der Encyclopedia of Laser Physics and Technology (englisch)
• Verschiedene Typen von Halbleiterlasern – Übersicht der verfügbaren Wellenlängen von Halbleiterlasern
• Sam’s Laser FAQ – Sammlung technischer Dokumentationen und Reparaturanleitungen (englisch)
• LaserFest – Website der American Physical Society anlässlich des 50. Jubiläums des Lasers (englisch)
• Laser – Licht in Formation, Video zum Laser auf Youtube, eingestellt von der Max-Planck-Gesellschaft
• Video: Was ist ein Laser?. Leibniz Universität Hannover 2011, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/393.

Siehe auch

• Liste der Lasertypen