Pivotverfahren
Pivotverfahren (auch Basisaustauschverfahren) sind Algorithmen der mathematischen Optimierung, insbesondere der linearen Optimierung. Für ein vorgegebenes System linearer Gleichungen in nichtnegativen Variablen (im Wesentlichen dasselbe wie ein System linearer Ungleichungen) wird nach der bestmöglichen von vielen Alternativlösungen (einer sogenannten Optimallösung) gesucht und auf dieser Suche das Gleichungssystem Schritt für Schritt umgewandelt, ohne dabei die Lösungsmenge zu verändern. Wichtige Pivotverfahren sind die Simplex-Verfahren und die Criss-Cross-Verfahren.
Pivotverfahren spielen für die Behandlung von linearen Ungleichungen eine analoge und ähnlich wichtige Rolle wie das gaußsche Eliminationsverfahren für die Lösung linearer Gleichungssysteme in unbeschränkten Variablen. Hauptanwendungsgebiet der Pivotverfahren ist die lineare Optimierung: sie gehören zu den meistverwendeten Lösungsmethoden in der Unternehmensforschung, der Wirtschaftswissenschaft, dem Gütertransport und sie werden auch in vielen anderen Gebieten wie im Ingenieurbau (Strukturoptimierung), in der Statistik (Regressionsanalyse) und in der Spieltheorie zunehmend eingesetzt.[1] Aufgaben mit zehntausenden Variablen und Ungleichungen sind an der Tagesordnung.[2]
Pivotansatz
Problemstellung
Ein Pivotverfahren geht immer von einem besonders gearteten linearen Gleichungssystem aus, in dem alle Variablen, außer vielleicht einer, nichtnegative Werte annehmen sollen. Jedes System linearer Ungleichungen oder Gleichungen, und auch jede lineare Optimierungsaufgabe, lässt sich nämlich in folgende (englisch dictionary genannte[3]) Buchform bringen:
Hier sind reelle (in der Praxis meist rationale) Zahlen. Die obige Notation soll aussagen, dass eine Lösung in den Unbekannten gesucht wird, welche die entsprechenden Gleichungen und Ungleichungen erfüllt und dabei die sogenannte Zielvariable so groß wie möglich wählt.
- ( Bei der Verwandlung der Aufgabe in die obige Form werden die Ungleichungen des Systems keinesfalls weniger: sie bleiben in mindestens gleicher Anzahl weiter vorhanden und treten nun als nichtnegative Variablen auf. Eine übliche lineare Ungleichung wie beispielsweise
- wird umgeformt in
- mit )
- ( Bei der Verwandlung der Aufgabe in die obige Form werden die Ungleichungen des Systems keinesfalls weniger: sie bleiben in mindestens gleicher Anzahl weiter vorhanden und treten nun als nichtnegative Variablen auf. Eine übliche lineare Ungleichung wie beispielsweise
Mit Hilfe der Indexmengen
lässt sich diese Aufgabe auch wie folgt in kompakter Form ausdrücken:
In jedem Schritt eines Pivotverfahrens ist wie oben eine Teilmenge der Variablen als unabhängig hervorgehoben, während die restlichen Variablen, Basisvariablen genannt, als linear-affine Funktionen der unabhängigen Variablen ausgedrückt werden. In aufeinanderfolgenden Schritten wechselt immer eine der Variablen von unabhängig auf Basisvariable und eine zweite in die umgekehrte Richtung; solche Variablenpaare werden Pivots genannt.
Optimumbedingungen
Falls im oben aufgestellten linearen Gleichungssystem die beiden folgenden Optimumbedingungen erfüllt sind,
- für alle (Zulässigkeit) und
- für alle (Zielbeschränkung),
dann kann man eine Lösung für die obige Aufgabe erhalten, indem man die unabhängigen Variablen auf die Werte setzt. Zum einen sind die Werte der freigelegten Variablen dann nichtnegativ, wie gefordert. Zum anderen dürfen sonstige mögliche Lösungen nur unabhängige Variable mit ebenfalls nichtnegativen Werten enthalten, so dass für jede dieser Lösungen die Ungleichung gilt.
- ( Im folgenden Beispielsystem,
- werden die Optimumbedingungen an zwei Stellen verletzt, da und ist. Zum ersten würde die Versuchslösung den negativen Wert enthalten, und zum zweiten könnte dessen Zielvariablenwert bei Lösungen mit unter Umständen erhöht werden. )
- ( Im folgenden Beispielsystem,
Austausch der Basisvariablen
Falls die Optimumbedingungen nicht erfüllt sind, was in der Regel der Fall sein wird, lässt sich das obige lineare Gleichungssystem aber auch andersartig ausdrücken, indem man an Stelle von eine andere, gleich große Teilmenge der Unbekannten auswählt und diese freilegt. Es sei eine Umstellung der Unbekannten. Anhand folgender Aufteilung der Variablen,
in neue unabhängige Variablen mit und neue Basisvariablen mit , wird das Gleichungssystem nun umgewandelt zu
wobei zu beachten ist, dass Einträge wie nur für Indexpaare mit und definiert sind. Die Einträge des so umgewandelten Gleichungssystems lassen sich nun erneut auf die Optimumbedingungen überprüfen,
- für alle (Zulässigkeit) und
- für alle (Zielbeschränkung),
was wiederum unter Umständen zu einer Lösung der Aufgabe führt.
Ein Standardergebnis der linearen Optimierung sagt aus[3][1], dass für jede lösbare Aufgabe ein Satz Basisvariablen existiert, der zu einer Lösung führt. Bei erfüllten Optimumbedingungen bilden die Basisvariablen eine sogenannte Optimalbasis des Systems.
Pivots und Pivotelemente
Jedes nichtverschwindende des obigen Gleichungssystems, dem Pivotsystem, nennt sich Pivotelement und erlaubt es, die unabhängige Variable an Stelle der Basisvariablen freizulegen, um so weiter nach einer Lösung zu suchen. Das ist die Vorgehensweise eines allgemeinen Pivotverfahrens, wobei aber nicht irgendwelche Pivotelemente gewählt werden, sondern nur erlaubte (admissible) Pivots , die Folgendes erfüllen müssen:
- Entweder gilt gleichzeitig und (Zulässigkeitspivot),
- oder es gilt gleichzeitig und (Zielfortschrittspivot).
- ( Im obigen Beispielsystem,
- sind wegen der Optimalitätsverletzung Pivotelement mit Pivot und Pivotelement mit Pivot erlaubt. Wegen der Optimalitätsverletzung sind aber ebenfalls Pivotelement mit Pivot , und Pivotelement mit Pivot erlaubt. )
- ( Im obigen Beispielsystem,
Die Beschränkung auf erlaubte Pivots verhindert, dass derselbe Pivot zweimal hintereinander ausgewählt wird. Die Regeln, nach denen in jedem Schritt eines dieser erlaubten Pivotelemente ausgewählt wird, hängen vom jeweiligen Verfahren ab; ein Mindestanspruch ist dabei natürlich, dass das Verfahren nach endlich vielen Schritten anhält, was bei ungeeigneter Auswahl von erlaubten Pivots nicht der Fall ist. Fukuda & Terlaky haben 1999 bewiesen, dass für jede lösbare Aufgabe und für jede Ausgangsbasis eine Folge von maximal erlaubten Pivots existiert, die zu einer Optimalbasis führt.[4] Leider liefert ihr Beweis keine Vorgehensweise, um diese Pivots in jedem Optimierungsschritt auch zu finden.
Wie aus der Definition zu ersehen ist, haben Optimalbasen keine erlaubten Pivots, das Verfahren kann in so einem Fall gar nicht fortgeführt werden. Anderseits kann anhand von Argumenten wie im obigen Abschnitt leicht gezeigt werden, dass eine nichtoptimale Basis ohne erlaubte Pivots immer zu einer Aufgabe gehört, die gar keine Lösung hat; entweder, weil das System der Gleichungen und Ungleichungen überhaupt keine Lösung hat (unzulässige Aufgabe), oder, weil sich Lösungen mit beliebig großem finden lassen (unbeschränkte Aufgabe).
Rundungsfehlerfreie Umsetzung
Um Rundungsfehler zu vermeiden, kann mit Bruchzahlen und gemeinsamen Nenner für sämtliche Einträge gearbeitet werden. Um in jedem Schritt einen gemeinsamen Nenner für das Gesamtsystem zu finden, müssen wir die Einträge nicht zusätzlich untersuchen. Falls das Startsystem ganzzahlig ist (was sich normalerweise durch Erweiterung erreichen lässt), gilt die Regel:
- Der Zähler des gewählten Pivotelements ist ein gemeinsamer Nenner für das darauffolgende System.
Wenn die Einträge des Folgesystems mit diesem gemeinsamen Nenner multipliziert werden, erhält man ganzzahlige Werte. Bei der Aufstellung des Folgesystems veraltet der gemeinsame Nenner des Vorgängersystems, weshalb sämtliche Einträge des Folgesystems ungeprüft durch diesen veralteten Nenner gekürzt werden können.
Eine Tabelle mit den Einträgen eines Pivotsystems wird oftmals Tableau genannt. Das folgende Schema zeigt an, wie sich die Einträge der Pivotsysteme von einem Schritt auf den nächsten verändern:
|
|
|
Das Zeichen steht hier für den gemeinsamen Nenner des Gleichungssystems, das Zeichen für den Zähler des Pivotelements, für einen sonstigen Eintrag der Pivotzeile, für einen sonstigen Eintrag der Pivotspalte, und für einen beliebigen Eintrag abseits von Pivotzeile und Pivotspalte. Einträge der Zielbeitragszeile () und der Basiswertspalte () werden nach denselben Regeln umgewandelt.
Beispiele
Zur grafischen Darstellung
Die Bilder zu den Schritten in den folgenden Beispielen zeigen alle dasselbe Gleichungssystem in verschiedenen orthogonalen Koordinaten; dabei gilt:
- Die grün umrandete Fläche ist der zulässige Bereich, in dem alle Variablen nichtnegative Werte haben.
- Koordinatenachsen entsprechen den Gleichungen von unabhängigen Variablen; sonstige Geraden beschreiben freigelegte Variablen.
- Schnittpunkte erlaubter Pivots sind rot markiert; der schwarzumrandete Schnittpunkt zeigt den ausgewählten Pivot.
- Die gelbe Fläche wird im nächsten Schritt zum nichtnegativen Quadranten.
Eine erfolgssichere Pivotauswahlregel
Wir wählen vorerst ein Beispiel ohne Zielvariable, das heißt, mit . In so einem Fall wird keine der Variablen maximiert; es werden nur beliebige (nichtnegative) Werte für die Unbekannten gesucht, die ein vorgegebenes Gleichungssystem erfüllen. In jedem Schritt wollen wir dann den erlaubten Pivot nach folgender Regel wählen:
- Wähle ,
- danach wähle .
Diese (nicht besonders effiziente) Auswahlregel fällt wegen mit der weiter unten angegebenen Kleinster-Index-Pivotauswahl zusammen; es lässt sich beweisen, dass diese Auswahl bei jeder lösbaren Aufgabe mit zu einer Optimalbasis führt.[5]
Wir suchen nun Werte für die Unbekannten , die das Gleichungssystem
erfüllen. Die erlaubten Pivots im obigen Gleichungssystem sind und ; aufgrund der obigen Auswahlregel legen wir die unabhängige Variable an Stelle der Basisvariablen frei:
 Basis 0 zu Basis 1 (animiertes SVG, nach Öffnung erneut anklicken und gedrückt halten; funktioniert nicht in allen Browsern)
Basis 0 zu Basis 1 (animiertes SVG, nach Öffnung erneut anklicken und gedrückt halten; funktioniert nicht in allen Browsern)
Wir erhalten nun das folgende, umgewandelte Gleichungssystem:
Im neuen System sind die erlaubten Pivots und ; dieses Mal legen wir legen wir an Stelle von frei:
 Basis 1 zu Basis 2 (animiertes SVG, nach Öffnung erneut anklicken und gedrückt halten; funktioniert nicht in allen Browsern)
Basis 1 zu Basis 2 (animiertes SVG, nach Öffnung erneut anklicken und gedrückt halten; funktioniert nicht in allen Browsern)
Wir erhalten nun das folgende System:
Der einzige erlaubte Pivot hier ist ; deshalb können wir nur an Stelle von freilegen:
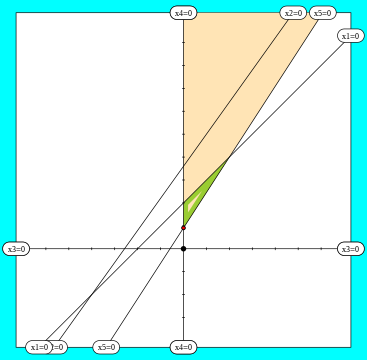 Basis 2 zu Basis 3 (animiertes SVG, nach Öffnung erneut anklicken und gedrückt halten; funktioniert nicht in allen Browsern)
Basis 2 zu Basis 3 (animiertes SVG, nach Öffnung erneut anklicken und gedrückt halten; funktioniert nicht in allen Browsern)
Nun erhalten wir
Dieses System erfüllt die Optimalitätsbedingungen und hat dementsprechend auch keine erlaubten Pivots. Indem wir sämtliche unabhängige Variablen auf Null setzen, erhalten wir die folgende Lösung:
Kreislaufanfällige Pivotauswahlregel
Es folgt nun ein Beispiel einer ungeeigneten Pivotauswahl; bei ungeeigneter Pivotwahl kann ein Pivotverfahren nämlich in einen unendlichen Kreislauf (eine Endlosschleife) geraten. Es sei wieder Wie bei folgender Regel vorgeschlagen, könnten wir beispielsweise der Versuchung erliegen, die Pivotzeile nur unter den "meistverletzten" Nebenbedingungen auszuwählen, und dabei "meistverletzt" als diejenigen mit den am weitesten negativen Konstanten verstehen:
- Wähle ,
- danach wähle .
Um zu zeigen, dass so etwas falsch gehen kann, starten wir mit dem System:
Wir wählen hier und legen an Stelle dessen frei. Dadurch erhalten wir das System:
Wir wählen Basisvariable , legen an deren Stelle frei, und erhalten:
Die Einträge in diesem Gleichungssystem sind dieselben wie im Startsystem, weshalb sich bei ähnlicher Pivotfolge auch die Einträge der folgenden Systeme alle zwei Schritte wiederholen werden. Nach Auswahl der Basisvariablen um an deren Stelle freizulegen erhalten wir:
Nach der kreislauffreien Regel im vorherigen Beispiel müssten wir nun wählen um freizulegen. Anstelle dessen folgen wir der abgewandelten Regel und wählen dafür die Basisvariable , was zu folgendem System führt:
Dieses Gleichungssystem hat dieselben Einträge wie das Startsystem. Weil diese nun anderen Variablen zugeordnet sind, ist die Endlosschleife nach diesen 4 Schritten freilich noch nicht beendet, aber die Umformung der Einträge ist hier unabhängig von deren Zuordnung zu Variablen, so dass nach endlich vielen Schritten (in diesem Falle 12) wieder das Startsystem erreicht wird. Das Gesamtsystem von Gleichungen und Ungleichungen hat in Wirklichkeit gar keine Lösung, doch kann das Pivotverfahren das mit der oberen Pivotwahl nicht herausfinden.
Die Reihenfolge, in der Variable und Gleichungen eines Pivotsystems aufgelistet werden, ist grundsätzlich willkürlich. Dennoch wurden die ersten Pivotauswahl-Strategien, die Variablen und Gleichungen unabhängig von deren Darstellung im Pivotsystem behandeln (und dazu noch leicht umsetzbar waren), erst 1977 von Bland [6] vorgestellt. In der Anfangszeit der Pivotverfahren (1950–1970), als noch nicht streng zwischen Algorithmen und Datenstrukturen unterschieden wurde, hat man Pivotauswahl-Strategien eher anhand von Datenstrukturen (der sogenannten Tableaus) beschrieben, und bei dieser Art Strategien konnte die Endlichkeit des Verfahrens ohne Zusatzberechnungen meist nicht gewährleistet werden.
Dualität
Duale Aufgabe
Jeder linearen Optimierungsaufgabe, welche in diesem Zusammenhang auch Primalaufgabe genannt wird, lässt sich von der obigen Buchform abhängig eine zweite Optimierungsaufgabe zuordnen; die Koeffizientenmatrix dieser sogenannten dualen Aufgabe ist die negative Transponierte der Koeffizientenmatrix der ursprünglichen Aufgabe:
In gedrungener Form wird das zu:
Wie gleich gezeigt wird, ist das Maximum der Dualaufgabe (soweit vorhanden) genau das negative Maximum der Primalaufgabe.
- (Vorsicht: Bei der Herleitung über diese Formulierung dürfen nicht durch ersetzt werden! Oftmals wird die duale Aufgabe auch mit der Zielfunktion anstelle von definiert, was zwar machbar, aber auch unübersichtlicher ist. )
Schrittweise Umwandlung
Die obige Beziehung der Koeffizienten zwischen Primalaufgabe und Dualaufgabe gilt nicht etwa nur für die Ausgangsbasis, sondern bleibt erhalten, solange die Basisvariablen nach denselben Pivots umgewandelt werden. Es gilt
Diese Dualitätsbeziehung lässt sich am leichtesten an einem Pivotsystem betrachten, das ausschließlich zwei unabhängige Unbekannte und zwei freigelegte Unbekannte enthält. Wir erhalten dasselbe System, wenn wir zuerst zwei der Unbekannten austauschen und danach die duale Aufgabe herleiten, oder wenn wir diese Schritte in umgekehrter Reihenfolge tun; das folgende kommutative Diagramm stellt diesen Zusammenhang dar:
|
|
| |
|
|
|
Aus der Dualbeziehung folgt, dass ein Optimalsystem für die Primalaufgabe auch einen Optimalsystem für die duale Aufgabe liefert.
Zur Aufgabe im ersten Rechenbeispiel gehört folgende duale Aufgabe (die Nullen stammen von ):
Der obige Algorithmus führt dann zum Optimalsystem
und die optimale Lösung dazu ist natürlich für alle . Die Primalaufgabe hatte eine implizite Zielfunktion ; sämtliche Optimallösungen der primalen und auch der dualen Aufgabe hätten deshalb, soweit vorhanden, einen Zielwert . Das ist derselbe Wert, den auch schon die Anfangslösung der dualen Aufgabe hatte, doch ist die Existenz einer Optimallösung aus dem ersten Gleichungssystem allein nicht ersichtlich: es hätte grundsätzlich auch Lösungen mit unendlich großem und somit gar keine Optimallösung geben können.
Lösungspaare
Eine theoretisch bedeutsame Folge der Dualitätstheorie ist: Wir brauchen nicht unbedingt einen Maximierungs-Algorithmus, um lineare Optimierungsprobleme zu lösen; es genügt dazu jeder Algorithmus, der Systeme linearer Ungleichungen löst. Aus der Dualitätsbeziehung folgt nämlich, dass jede Optimalbasis der ursprünglichen Aufgabe auch unmittelbar eine Optimalbasis für die duale Aufgabe liefert; der optimale Wert der Zielvariable ist dann das Negative des Optimalwerts von . Für zulässige Lösungspaare der beiden Aufgaben gilt demzufolge
und für optimale Lösungspaare gilt
Daraus folgt, dass die optimalen Lösungen beider Aufgaben genau die Lösungen der obigen Gleichungssysteme mit folgenden Ungleichungen sind:
Ausgeschrieben ist das
In der Praxis ist so ein Vorgehen freilich nur dann konkurrenzfähig, wenn die gemeinsame Datenstruktur beider Aufgaben auch ausgenützt wird.
Spezielle Pivotverfahren
Die einfachsten aller Pivotverfahren gehören zu den Criss-Cross-Verfahren[5], die in den 80er Jahren für Aufgabenstellungen im Kontext orientierter Matroide entwickelt wurden. Die wesentlich komplexeren Simplexverfahren[3][1] wurden aber bereits 1947 von George Dantzig für die Lösung linearer Optimierungsprobleme veröffentlicht und haben danach dank ihrer weiten Verbreitung die Suche nach Criss-Cross-Verfahren maßgeblich motiviert. Weitere Pivotverfahren wurden für das lineare Komplementaritätsproblem mit suffizienten Matrizen (einschließlich quadratischer Programmierung) und für linear-fraktionale Optimierungsprobleme entwickelt.
Bei der Ausarbeitung verschiedener Pivotverfahren geht es in der Hauptsache darum, die Anzahl der Pivotschritte und damit auch die Laufzeit des Verfahrens gering zu halten. Während die derzeit bekannten Simplexverfahren alle eine überpolynomial beschränkte Laufzeit beanspruchen – das ist eine Laufzeit, die sich nicht durch ein Polynom in der Datenspeichergröße beschränken lässt – sind Laufzeitschranken für die Criss-Cross-Verfahren ein (bis 2010) noch offenes Forschungsthema.[7] Zusammenfassend lässt sich darüber sagen, dass Criss-Cross-Verfahren mehr Freiheitsgrade aufweisen als Simplexverfahren, und dass ein Criss-Cross-Verfahren genau aus diesem Grund bei einer guten Pivotauswahl schneller[4] und bei einer schlechten Pivotauswahl langsamer[8] als Simplexverfahren sein kann.
Primale Simplexverfahren
Primale Simplexverfahren (meist nur Simplexverfahren genannt) gehen von einer sogenannten zulässigen Basis mit für alle aus und untersuchen ausschließlich zulässige Basen, bis eine Optimalbasis gefunden wird. Eine wichtige Eigenschaft der primalen Simplexverfahren ist, dass der Wert der Zielvariablen, also , mit jedem Schritt monoton anwächst; würde er streng monoton anwachsen, wäre die Endlichkeit des Verfahrens gesichert.
Ein primales Simplexverfahren muss seine Pivots wie folgt wählen:
- Wähle ein beliebiges , das erfüllt. Zum Beispiel, suche das kleinste mit dieser Eigenschaft (Bland-Regel[6]).
- Wähle ein beliebiges , das erfüllt. Zum Beispiel, suche das kleinste mit dieser Eigenschaft (Bland-Regel).
Um eine zulässige Ausgangsbasis zu erhalten, muss in einer sogenannten Phase 1 eine Hilfsaufgabe gelöst werden. Dies kann geschehen, indem man eine neue Zielfunktion mit beliebigen nichtpositiven Einträgen einfügt und die duale Aufgabe, bei der die Startlösung nun zulässig ist, maximiert. Statistisch gesehen ist es von Vorteil, die Einträge der neuen Zielfunktion zufallsverteilt negativ auszuwählen.[1]
Ein Standardergebnis der linearen Optimierung besagt[3][1], dass für jede lösbare Aufgabe und für jede zulässige Basis eine Folge erlaubter Pivots existiert, die über ausschließlich zulässige Basen zu einer Optimalbasis führt; unbekannt ist dagegen, ob es eine Folge dieser Art gibt, deren Länge sich polynomial in der Speichergröße der Daten beschränken lässt.
Duale Simplexverfahren
Duale Simplexverfahren sind Pivotverfahren, die von einer sogenannten dual-zulässigen Basis mit für alle ausgehen und in ihrer Suche nach einer Optimalbasis ausschließlich dual-zulässige Basen untersuchen; der Wert der Zielvariablen nimmt dabei monoton ab.
Ein duales Simplexverfahren wählt seine Pivots wie folgt:
- Wähle ein beliebiges , das erfüllt. Zum Beispiel, suche das kleinste mit dieser Eigenschaft (Bland-Regel [6]).
- Wähle ein beliebiges , das erfüllt. Zum Beispiel, suche das kleinste mit dieser Eigenschaft (Bland-Regel).
Duale Simplexverfahren erzeugen die gleichen Pivotfolgen wie die auf die duale Aufgabe angewandten primalen Simplexverfahren und haben deshalb auch grundsätzlich die gleichen Eigenschaften wie die primalen Verfahren. Dass sie für die Lösung vieler angewandter Aufgaben trotzdem den Primalverfahren vorgezogen werden, liegt daran, dass es für viele angewandte Aufgaben leichter ist, eine dual-zulässige Ausgangsbasis zu finden.
Criss-Cross-Verfahren
Criss-Cross-Verfahren (englisch: kreuz und quer) sind allgemeine Pivotverfahren, die von einer beliebigen Basis ausgehen[5]; in der Regel wird dieser Name für kombinatorische Pivotverfahren verwendet, das heißt, für Pivotverfahren, welche nur die Vorzeichen der Systemkoeffizienten und nicht die Koeffizienten selbst für die Pivotauswahl in Betracht ziehen.
Das bekannteste aller Criss-Cross-Verfahren erweitert die Kleinster-Index-Pivotauswahl aus dem ersten Beispiel.[5] Dafür werden die Unbekannten in einer mehr oder weniger festen Reihenfolge angeordnet und die Pivots wie folgt ausgewählt (wie üblich sei das Minimum der leeren Menge unendlich groß):
- Suche die Indices und .
- Falls , ist, wähle Pivot mit .
- Falls , ist, wähle Pivot mit .
Das lässt natürlich die Frage offen, wie die Variablen angeordnet werden sollen.
Beispiel eines Criss-Cross-Verfahrens
Im folgenden Beispiel benutzen wir die obige Kleinster-Index-Pivotauswahl. Es sollen Werte für die Variablen gefunden werden, die das Gleichungssystem
erfüllen und dabei die zusätzliche Zielvariable auf ein Maximum bringen. Wir benutzen dazu die oben angeführte Pivotauswahl des kleinsten Index.
In unserem Ausgangssystem sind sämtliche Pivots erlaubt; die Auswahlregel schreibt aber vor, dass wir freilegen und gegen austauschen:
 Basis 0 zu Basis 1 (animiertes SVG, nach Öffnung erneut anklicken und gedrückt halten; funktioniert nicht in allen Browsern)
Basis 0 zu Basis 1 (animiertes SVG, nach Öffnung erneut anklicken und gedrückt halten; funktioniert nicht in allen Browsern)
Das führt zum neuen Gleichungssystem:
Hier sind die Pivots , und , erlaubt; anhand der Auswahlregel legen wir an Stelle von frei:
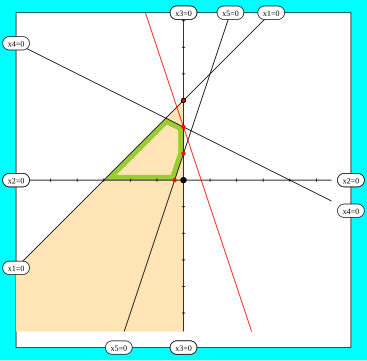 Basis 1 zu Basis 2 (animiertes SVG, nach Öffnung erneut anklicken und gedrückt halten; funktioniert nicht in allen Browsern)
Basis 1 zu Basis 2 (animiertes SVG, nach Öffnung erneut anklicken und gedrückt halten; funktioniert nicht in allen Browsern)
Wir erhalten das System:
Die erlaubten Pivots dieses Gleichungssystems sind und ; wir legen darum an Stelle von frei:
 Basis 2 zu Basis 3 (animiertes SVG, nach Öffnung erneut anklicken und gedrückt halten; funktioniert nicht in allen Browsern)
Basis 2 zu Basis 3 (animiertes SVG, nach Öffnung erneut anklicken und gedrückt halten; funktioniert nicht in allen Browsern)
Nun erhalten wir das System:
Dieses Gleichungssystem ist optimal; die Werte der Unbekannten für die dazugehörige Lösung sind
Große Aufgaben
Eine Implementierung der Pivotverfahren für praktische Aufgaben ist oft weit von trivial entfernt.[9] Die Einträge großer Gleichungssysteme – mit zehntausenden von Variablen – weisen so gut wie immer irgendeine Struktur auf, die es auszunutzen gilt, um die Berechnung derselben schnell und rundungsfehlerarm durchzuführen:
- Im Startsystem großer Aufgaben (nicht in den umgewandelten Gleichungssystemen) ist die überwältigende Mehrheit der Einträge Null (das System ist dünnbesetzt), was es ermöglicht, einen Großteil der Rechnungen einzusparen, wenn man auch in späteren Umwandlungen teilweise vom Startsystem ausgeht.
- Bei den Vorgehensweisen mit verzögerter Auswertung (über Umstellung der Startmatrix, teilweise LR-Zerlegung der Koeffizientenmatrix, Produktform inverser Matrizen und anderem mehr) berechnet man einen Eintrag nur und erst dann, wenn man ihn wirklich braucht, um den Pivot zu finden. Dabei muss man aber oft auf Einträge aus älteren Gleichungssystemen zurückgreifen, so dass die Formeln zur Berechnung komplizierter und vielfältiger werden.
- Für manche Sonderstrukturen, wie zum Beispiel dem Netzflussproblem,[3][10] wurden besonders effiziente Umsetzungen entwickelt, und diese Sonderstrukturen sind oft eingebettet in größere Systeme.
Nichtsdestominder kommen in der Praxis auch kleinere Aufgaben vor, für welche die oben beschriebene Direktumsetzung durchaus sinnvoll ist.
Literatur
- George B. Dantzig: Lineare Programmierung und Erweiterungen (= Ökonometrie und Unternehmensforschung. Band 2). Springer, Berlin u. a. 1966 (Originalausgabe: Linear Programming and Extensions. Princeton University Press, Princeton NJ 1963, (PDF; 9,1 MB)).
- Vašek Chvátal: Linear Programming. Freeman and Company, New York NY 1983, ISBN 0-7167-1587-2.
- Robert J. Vanderbei: Linear Programming. Foundations and Extensions (= International Series in Operations Research & Management Science. Band 114). 3. Auflage. Springer, New York NY 2007, ISBN 978-0-387-74387-5 ((PDF; 2,3 MB), Alternativausgabe: Linear Programming; Foundations and Extensions, Kluwer, ISBN 978-0-7923-9804-2).
Einzelnachweise
- ↑ a b c d e Robert Vanderbei: Linear Programming. Foundations and Extensions (= International Series in Operations Research & Management Science. Bd. 114). 3rd edition. Springer, New York NY 2007, ISBN 978-0-387-74387-5.
- ↑ Robert Vanderbei: Linear Programming. Foundations and Extensions (= International Series in Operations Research & Management Science. Bd. 114). 3rd edition. Springer, New York NY 2007, ISBN 978-0-387-74387-5, Kapitel 21.4: Simplex Method vs Interior-Point Methods.
- ↑ a b c d e Vašek Chvátal: Linear Programming. Freeman and Company, New York NY 1983, ISBN 0-7167-1587-2.
- ↑ a b Komei Fukuda, Tamás Terlaky: On the Existence of a Short Admissible Pivot Sequences for Feasibility and Linear Optimization Problems. In: Pure Mathematics and Applications. Bd. 10, 1999, ISSN 1218-4586, S. 431–447, (PDF).
- ↑ a b c d Komei Fukuda, Tamás Terlaky: Criss-cross methods: A fresh view on pivot algorithms. In: Mathematical Programming. Bd. 79, Nr. 1/3, 1997, ISSN 0025-5610, S. 369–395, doi:10.1007/BF02614325, ps-Datei (Seite nicht mehr abrufbar, Suche in Webarchiven) Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis. .
- ↑ a b c Robert G. Bland: New finite pivoting rules for the simplex method. In: Mathematics of Operations Research. Bd. 2, Nr. 2, S. 103–107, doi:10.1287/moor.2.2.103.
- ↑ Shuzhong Zhang: New variants of finite criss-cross pivot algorithms for linear programming. In: European Journal of Operations Research. Bd. 116, Nr. 3, 1999, ISSN 0377-2217, S. 607–614, doi:10.1016/S0377-2217(98)00026-5, (PDF; 164,4 kB).
- ↑ Komei Fukuda & Bohdan Kaluzny: The criss-cross method can take Ω(nd) pivots. In: Proceedings of the Twentieth Annual Symposium on Computational Geometry (SCG '04). June 9 – 11, 2004, Brooklyn, New York, USA. ACM Press, New York NY 2004, ISBN 1-58113-885-7, S. 401–408, doi:10.1145/997817.997877, ps-Datei (Memento des Originals vom 17. September 2013 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis..
- ↑ Robert Vanderbei: Linear Programming. Foundations and Extensions (= International Series in Operations Research & Management Science. Bd. 114). 3rd edition. Springer, New York NY 2007, ISBN 978-0-387-74387-5, Kapitel 8: Implementation Issues.
- ↑ Robert Vanderbei: Linear Programming. Foundations and Extensions (= International Series in Operations Research & Management Science. Bd. 114). 3rd edition. Springer, New York NY 2007, ISBN 978-0-387-74387-5, Kapitel 13: Network Flow Problems.
Weblinks
- Interaktives Pivotverfahren-Applet von Robert Vanderbei aus dem Jahr 1997. Das Applet erlaubt dem Benutzer, ein lineares Gleichungssystem mit freigelegten Basisvariablen aufzustellen und anschließend beliebige Variablen dieses Gleichungssystems umzustellen. Obwohl sich das Applet „Simplex Pivot Tool“ nennt, ist es auf ganz allgemeine Pivotverfahren ausgerichtet. Die Koeffizienten können auch rundungsfrei als Bruchzahlen eingesehen werden, werden aber nicht auf einen gemeinsamen Nenner gebracht.
- Zusatzinfo zum Criss-Cross-Verfahren (englische Wikipedia).
![{\displaystyle {\begin{matrix}z&=&f&+&~~~~~d_{1}\,x_{1}&+&\cdots &+&~~~~~d_{n}\,x_{n}\\[3pt]x_{n+1}&=&b_{n+1}&+&G_{n+1,1}\,x_{1}&+&\cdots &+&G_{n+1,n}\,x_{n}\\\vdots &&\vdots &&\vdots &&&&\vdots \\x_{n+m}&=&b_{n+m}&+&G_{n+m,1}\,x_{1}&+&\cdots &+&G_{n+m,n}\,x_{n}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f09bbf72db1fcfbcd303a394cd2b9d896d89c800)








![{\displaystyle {\begin{matrix}&&z&=&f&+&\sum _{j\in D}\,d_{j}\,x_{j}\\[6pt]\forall ~i\in B&&x_{i}&=&b_{i}&+&\sum _{j\in D}\,G_{i,j}\,x_{j}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/794d9b6a3388e029e919524b86bb0475a800bf25)








![{\displaystyle {\begin{matrix}z&=&~~~0&-~3x_{1}&+~~\mathbf {x_{2}} \\[2pt]x_{3}&=&~~~3&-~~x_{1}&-~~x_{2}\\[2pt]x_{4}&=&~~~8&+~2x_{1}&-~4x_{2}\\[2pt]x_{5}&=&-~\mathbf {1} &+~3x_{1}&+~~x_{2}\,,\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83ee0a46614d4a24aa32b5c07167f58b0d55db10)














![{\displaystyle {\begin{matrix}&&z&=&f^{\pi }&+&\sum _{j\in D(\pi )}\,d_{j}^{\pi }\,x_{j}\\[6pt]\forall ~i\in B(\pi )&&x_{i}&=&b_{i}^{\pi }&+&\sum _{j\in D(\pi )}\,G_{i,j}^{\pi }\,x_{j}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a94ebfb6ee88e4f6b35e70a0a1e7a810390755e1)












![{\displaystyle {\begin{matrix}z&=&~~~0&-~3x_{1}&+~~~\mathbf {x_{2}} \\[2pt]x_{3}&=&~~~3&-~~x_{1}&-~~~{\underline {\mathbf {x_{2}} }}\\[2pt]x_{4}&=&~~~8&+~2x_{1}&-~{\underline {\mathbf {4x_{2}} }}\\[2pt]x_{5}&=&-~\mathbf {1} &+~{\underline {\mathbf {3x_{1}} }}&+~~~{\underline {\mathbf {x_{2}} }}\,,\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8843209cdeaf836610ea941fe382442894fe35aa)










![{\displaystyle {\begin{matrix}\delta \,x_{i}&\!=\!&(~~\alpha )&\!\!\!x_{j}&\!+\!&(~~\sigma )&\!\!\!x_{s}\\[6pt]\delta \,x_{r}&\!=\!&(~~\zeta )&\!\!\!x_{j}&\!+\!&(~~p)&\!\!\!x_{s}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d0c16c9d414104fbef3eece921fac518843e3e8)

![{\displaystyle {\begin{matrix}p\,x_{i}&\!=\!&(\textstyle {\frac {\alpha p\,-\,\zeta \sigma }{\delta }})&\!\!\!x_{j}&\!+\!\!&(~\sigma )&\!\!\!x_{r}\\[6pt]p\,x_{s}&\!=\!&(~-\zeta ~)&\!\!\!x_{j}&\!+\!\!&(~\delta )&\!\!\!x_{r}\\\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de60e809db57a4b70121bd2c1b367a6d9cafae7a)














![{\displaystyle {\begin{matrix}x_{3}&=&(&-~\mathbf {2} &-~7x_{1}&+~{\underline {\mathbf {2x_{2}} }}&)~/~1\\[2pt]x_{4}&=&(&-~4&-~5x_{1}&+~2x_{2}&)~/~1\\[2pt]x_{5}&=&(&~~~9&+~2x_{1}&-~3x_{2}&)~/~1\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d756f762e61c4a8d485295c611df8c1dfdc1d13c)


![{\displaystyle {\begin{matrix}x_{2}&=&(&~~~2&+~~7x_{1}&+~~~~x_{3}&)~/~2\\[2pt]x_{4}&=&(&-~\mathbf {4} &+~~{\underline {\mathbf {4x_{1}} }}&+~~~2x_{3}&)~/~2\\[2pt]x_{5}&=&(&~~12&-~17x_{1}&-~~~3x_{3}&)~/~2\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b989c48f52ce7c22d6a52b0687d34abed75ecd75)




![{\displaystyle {\begin{matrix}x_{2}&=&(&~~18&+~~7x_{4}&-~~5x_{3}&)~/~4\\[2pt]x_{1}&=&(&~~~4&+~~2x_{4}&-~~2x_{3}&)~/~4\\[2pt]x_{5}&=&(&-\mathbf {10} &-~17x_{4}&+~{\underline {\mathbf {11x_{3}} }}&)~/~4\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a751d58c9c09942b25037b36dba943c0ed6a049)


![{\displaystyle {\begin{matrix}x_{2}&=&(&~~37&-~~2x_{4}&-~~~5x_{5}&)~/~11\\[2pt]x_{1}&=&(&~~~6&-~~3x_{4}&-~~~2x_{5}&)~/~11\\[2pt]x_{3}&=&(&~~10&+~17x_{4}&+~~~4x_{5}&)~/~11\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5659c33c9714cce76035a79f2832736b8dc06fb3)



![{\displaystyle {\begin{matrix}x_{3}&=&(&-~\mathbf {2} &+~~{\underline {\mathbf {x_{1}} }}&+~~x_{2}&)~/~2\\[2pt]x_{4}&=&(&~~~6&-~7x_{1}&-~3x_{2}&)~/~2\\[2pt]x_{5}&=&(&~~~0&-~3x_{1}&-~~x_{2}&)~/~2\\[2pt]x_{6}&=&(&~~~4&+~7x_{1}&+~~x_{2}&)~/~2\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3e08ba99842d1c0bf118ad3e24560626005ddf0)


![{\displaystyle {\begin{matrix}x_{1}&=&(&~~~2&+~2x_{3}&-~~x_{2}&)~/~1\\[2pt]x_{4}&=&(&-~\mathbf {4} &-~7x_{3}&+~{\underline {\mathbf {2x_{2}} }}&)~/~1\\[2pt]x_{5}&=&(&-~~3&-~3x_{3}&+~~x_{2}&)~/~1\\[2pt]x_{6}&=&(&~~~9&+~7x_{3}&-~3x_{2}&)~/~1\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4404997705ea0deb944cb8483e14a899e122e98e)


![{\displaystyle {\begin{matrix}x_{1}&=&(&~~~0&-~3x_{3}&-~~x_{4}&)~/~2\\[2pt]x_{2}&=&(&~~~4&+~7x_{3}&+~~x_{4}&)~/~2\\[2pt]x_{5}&=&(&-~\mathbf {2} &+~~{\underline {\mathbf {x_{3}} }}&+~~x_{4}&)~/~2\\[2pt]x_{6}&=&(&~~~6&-~7x_{3}&-~3x_{4}&)~/~2\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d89bbc937f287b16f0b778ebbee70ce21694b407)

![{\displaystyle {\begin{matrix}x_{1}&=&(&-~~3&-~3x_{5}&+~~x_{4}&)~/~1\\[2pt]x_{2}&=&(&~~~9&+~7x_{5}&-~3x_{4}&)~/~1\\[2pt]x_{3}&=&(&~~~2&+~2x_{5}&-~~x_{4}&)~/~1\\[2pt]x_{6}&=&(&-~\mathbf {4} &-~7x_{5}&+~{\underline {\mathbf {2x_{4}} }}&)~/~1\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fbc097ee338568de5244e3429720f4237861e51)

![{\displaystyle {\begin{matrix}x_{1}&=&(&-~\mathbf {2} &+~~{\underline {\mathbf {x_{5}} }}&+~~x_{6}&)~/~2\\[2pt]x_{2}&=&(&~~~6&-~7x_{5}&-~3x_{6}&)~/~2\\[2pt]x_{3}&=&(&~~~0&-~3x_{5}&-~~x_{6}&)~/~2\\[2pt]x_{4}&=&(&~~~4&+~7x_{5}&+~~x_{6}&)~/~2\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d3df86e20144c7af36b4ce61a75fc56d64942bd)
![{\displaystyle {\begin{matrix}w&=&-\;f&-&b_{1}\,y_{n+1}&-&\cdots &-&b_{m}\,y_{n+m}\\[3pt]y_{1}&=&-\;d_{1}&-&G_{n+1,1}\,y_{n+1}&-&\cdots &-&G_{n+m,1}\,y_{n+m}\\\vdots &&\vdots &&\vdots &&&&\vdots \\y_{n}&=&-\;d_{n}&-&G_{n+1,n}\,y_{n+1}&-&\cdots &-&G_{n+m,n}\,y_{n+m}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b69740dc2bd698664779fec772dc9aed203779e8)

![{\displaystyle {\begin{matrix}&&w&=&(-f)&+&\sum _{i\in B}\,(-b_{i})\,y_{i}\\[6pt]\forall ~j\in D&&y_{j}&=&(-d_{j})&+&\sum _{i\in B}\,(-G_{i,j})\,y_{i}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97cfb41d976d5ca7639dc59afeacdb2b9f21e7a3)





![{\displaystyle {\begin{matrix}&&w&=&(-f^{\pi })&+&\sum _{i\in B(\pi )}\,(-b_{i}^{\pi })\,y_{i}\\[6pt]\forall ~j\in D(\pi )&&y_{j}&=&(-d_{j}^{\pi })&+&\sum _{i\in B(\pi )}\,(-G_{i,j}^{\pi })\,y_{i}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc04bdbd82b7b93d78f6266c3f911ef2f00c1b18)

![{\displaystyle -\,[\cdots ]^{\,T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2331baecd2351bac704e20ba3665c9d89f7cf742)
![{\displaystyle {\begin{matrix}\delta \,y_{j}&\!=\!&(-\alpha )&\!\!\!y_{i}&\!+\!&(-\zeta )&\!\!\!y_{r}\\[6pt]\delta \,y_{s}&\!=\!&(-\sigma )&\!\!\!y_{i}&\!+\!&(-p)&\!\!\!y_{r}\\\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca3a749640a8ec5915c25e4f9ce875b77e426708)

![{\displaystyle {\begin{matrix}p\,y_{j}&\!=\!&(\textstyle {\frac {\zeta \sigma \,-\,\alpha p}{\delta }})&\!\!\!y_{i}&\!+\!\!&(~~\zeta )&\!\!\!y_{s}\\[6pt]p\,y_{r}&\!=\!&(~-\sigma ~)&\!\!\!y_{i}&\!+\!\!&(-\delta )&\!\!\!y_{s}\\\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c489d21e80a4c5509a6ff8dde5f8c1d495082b9)

![{\displaystyle {\begin{matrix}~w~&=&(&0&+~~2y_{3}&+~~4y_{4}&-~~9y_{5}&)~/~1\\[2pt]y_{1}&=&(&0&+~~7y_{3}&+~~5y_{4}&-~~2y_{5}&)~/~1\\[2pt]y_{2}&=&(&0&-~~2y_{3}&-~~2y_{4}&+~~3y_{5}&)~/~1\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00761975e87bc2c13f59b2048169bb46766caeb7)

![{\displaystyle {\begin{matrix}~w~&=&(&0&-~37y_{2}&-~~6y_{1}&-~10y_{3}&)~/~11\\[2pt]y_{4}&=&(&0&+~~2y_{2}&+~~3y_{1}&-~17y_{3}&)~/~11\\[2pt]y_{5}&=&(&0&+~~5y_{2}&+~~2y_{1}&-~~4y_{3}&)~/~11\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6d31ca0cbfa88fec9ad8c5ab0dae7f7b7fbedb9)







![{\displaystyle {\begin{matrix}\sum _{j\in D}\,d_{j}\,x_{j}~~+~~\sum _{i\in B}\,(-b_{i})\,y_{i}~~\geq ~~0\\[6pt]\forall ~j\in D\quad y_{j}~=~(-d_{j})~+~\sum _{i\in B}\,(-G_{i,j})\,y_{i}\\[6pt]\forall ~i\in B\quad x_{i}~=~b_{i}~+~\sum _{j\in D}\,G_{i,j}\,x_{j}\\[6pt]\forall ~k\in D\cup B\qquad x_{k}\geq 0,\quad y_{k}\geq 0\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a807537746eba2740941f39ffd167af0ceb104d4)












![{\displaystyle {\begin{matrix}z&=&(&~~~0&+~\mathbf {3x_{1}} &+~2x_{2}&)~/~1\\[2pt]x_{3}&=&(&~~~3&-~{\underline {\mathbf {2x_{1}} }}&-~~x_{2}&)~/~1\\[2pt]x_{4}&=&(&~~~7&-~2x_{1}&-~3x_{2}&)~/~1\\[2pt]x_{5}&=&(&~~~4&-~3x_{1}&-~~x_{2}&)~/~1\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bcc63ee2d5f4d8bb3003f632c6dbe3ea4541810)
![{\displaystyle {\begin{matrix}z&=&(&~~~9&-~3x_{3}&+~~\mathbf {x_{2}} &)~/~2\\[2pt]x_{1}&=&(&~~~3&-~~x_{3}&-~~{\underline {\mathbf {x_{2}} }}&)~/~2\\[2pt]x_{4}&=&(&~~~8&+~2x_{3}&-~4x_{2}&)~/~2\\[2pt]x_{5}&=&(&-~1&+~3x_{3}&+~~x_{2}&)~/~2\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a285d35f38bfe29a9baca8d5b20cec6888440d5)


![{\displaystyle {\begin{matrix}z&=&(&~~~6&-~2x_{3}&-~~x_{1}&)~/~1\\[2pt]x_{2}&=&(&~~~3&-~~x_{3}&-~2x_{1}&)~/~1\\[2pt]x_{4}&=&(&-~\mathbf {2} &+~3x_{3}&+~{\underline {\mathbf {4x_{1}} }}&)~/~1\\[2pt]x_{5}&=&(&~~~1&+~~x_{3}&-~~x_{1}&)~/~1\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dff1b909d574f9103748c18887d53444e59bf8a)
![{\displaystyle {\begin{matrix}z&=&(&~~22&-~5x_{3}&-~~x_{4}&)~/~4\\[2pt]x_{2}&=&(&~~~8&+~2x_{3}&-~2x_{4}&)~/~4\\[2pt]x_{1}&=&(&~~~2&-~3x_{3}&+~~x_{4}&)~/~4\\[2pt]x_{5}&=&(&~~~2&+~7x_{3}&-~~x_{4}&)~/~4\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7b5b1771b7e0080cfc88f743adb231e1b5a51d6)
