Reihe (Mathematik)

Die Reihe ${\tfrac {1}{2}}+{\tfrac {1}{4}}+{\tfrac {1}{8}}+\cdots$ konvergiert gegen 1

Eine Reihe, selten Summenfolge oder unendliche Summe und vor allem in älteren Darstellungen auch unendliche Reihe genannt, ist ein Objekt aus dem mathematischen Teilgebiet der Analysis. Anschaulich ist eine Reihe eine Summe mit unendlich vielen Summanden. Präzise wird eine Reihe als eine Folge definiert, deren Glieder die Partialsummen einer anderen Folge sind. Wenn man die Zahl 0 zur Indexmenge zählt, ist die $n$-te Partialsumme die Summe der ersten $n+1$ (von den unendlich vielen) Summanden. Falls die Folge dieser Partialsummen einen Grenzwert besitzt, so wird dieser der Wert oder die Summe der Reihe genannt.

Definition

Für reelle und komplexe Folgen

Ist eine beliebige reelle (oder komplexe) Folge $\left(a_{j}\right)_{j\in \mathbb {N} _{0}}$ gegeben, kann man aus ihr eine neue Folge $\left(s_{n}\right)_{n\in \mathbb {N} _{0}}$ der Partialsummen bilden. Die $n$-te Partialsumme ist die Summe der ersten $n+1$ Glieder von $\left(a_{j}\right)_{j\in \mathbb {N} _{0}}$, ihre Definition lautet:

$s_{n}:=a_{0}+a_{1}+\dotsb +a_{n}.$

Die Folge $\left(s_{n}\right)_{n\in \mathbb {N} _{0}}$ der $n$-ten Partialsummen heißt Reihe. Falls die Reihe (also die Folge der Partialsummen) konvergiert, so nennt man ihren Grenzwert

$\lim _{n\to \infty }s_{n}=\lim _{n\to \infty }\sum _{j=0}^{n}a_{j}$

den Wert der Reihe oder die Summe der Reihe. Dieser ist eindeutig bestimmt und wird meistens als $\sum _{j=0}^{\infty }a_{j}$ notiert.

Zu bemerken ist, dass aus der Definition folgt, dass andersherum jede Zahlenfolge $a_{0},a_{1},a_{2},a_{3},\dots$ zu einer Reihe wird, wenn man diese als Partialsummen der Folge $a_{0},(a_{1}-a_{0}),(a_{2}-a_{1}),(a_{3}-a_{2}),\dots$ auffasst. Eine Reihe ist also nichts anderes als eine Folge spezieller „Bauart“, deren Glieder rekursiv durch $s_{0}:=a_{0}$ und $s_{n+1}:=s_{n}+a_{n+1}$ definiert sind. Allerdings führt die einfache rekursive Struktur der Reihen zu sehr handlichen Konvergenzkriterien.

Definition über Banachräume

Es sei $E$ ein Banachraum und $(x_{j})_{j\in \mathbb {N} _{0}}$ eine Folge in $E$. Dann definieren wir eine neue Folge $(s_{n})_{n\in \mathbb {N} _{0}}$ in $E$ durch

$s_{n}:=\sum _{j=0}^{n}x_{j}.$

Diese heißt Reihe in $E$. Sie heißt konvergent, wenn die Folge der Partialsummen konvergiert, wobei hier die zu $E$ gehörige Norm $|.|_{E}$ genutzt wird. Auch in diesem Fall gilt die oben erklärte Korrespondenz zwischen Folgen und Reihen, wobei erneut die rekursive Bauart zu Vorteilen bei der Formulierung von Konvergenzkriterien führt.

Notation

Für Reihen gibt es je nach Kontext unterschiedliche Notationen. In diesem Artikel werden als Indizes für die Glieder von Folge und Reihe die natürlichen Zahlen einschließlich der Null verwendet. Bei manchen Anwendungen ist es zweckmäßig, die Summation erst beim Index 1, 2 oder höher zu beginnen, selten kommen auch negative Indizes vor (siehe Laurent-Reihe). Mit Hilfe des Summenzeichens können die einzelnen Glieder der Reihe auch abgekürzt als

$s_{n}=\sum _{i=0}^{n}a_{i}$

geschrieben werden. Ebenso geht man bei der Folge der Einzelglieder vor und schreibt kurz

$S=\sum _{i=0}^{\infty }a_{i}.$

Häufig werden ein Teil oder alle Indizes weggelassen, wenn Missverständnisse ausgeschlossen sind. Ist etwa wie hier im Kontext von Berechnungen mit unendlichen Reihen klar, dass generell bei 0 zu nummerieren angefangen wird, so steht

$S=\sum a_{i}$ für $S=\sum _{i=0}^{\infty }a_{i}.$

Auswertung und Einteilung

Wenn $(a_{i})$ und damit auch $(s_{n})$ für alle nichtnegativen ganzen Indizes i bzw. n definiert sind, lässt sich somit eine unendliche Reihe bilden: wenn der Grenzwert der Folge der Partialsummen

$S=\lim _{n\rightarrow \infty }s_{n}=\lim _{n\rightarrow \infty }\left(\sum _{i=0}^{n}a_{i}\right)$

existiert, sagt man, die Reihe konvergiert; den Grenzwert S nennt man die Summe der Reihe oder den Wert der Reihe. Mit Hilfe des Summenzeichens kann diese Summe auch abgekürzt als

$S=\sum _{i=0}^{\infty }a_{i}$

geschrieben werden.

Eine Reihe $(s_{n})$ heißt divergent oder ihr Grenzwert nicht existent, wenn die Reihe nicht konvergiert. Sie heißt bestimmt divergent oder uneigentlich konvergent, wenn die Teilsummen $(s_{n})$ gegen −∞ oder +∞ streben. Andernfalls heißt die Reihe unbestimmt divergent; dabei kann sie Häufungspunkte haben oder auch nicht.

Mit verschiedenen Konvergenzkriterien lässt sich feststellen, ob eine Reihe konvergiert.

Beispiele

Die geometrische Reihe $\sum _{k=0}^{\infty }r^{k}$ für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r=\tfrac 12} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r=\tfrac 13} oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r=\tfrac 14} konvergiert

Eine klassische Reihe ist die geometrische Reihe, der Name ergibt sich aus der geometrischen Folge (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_n = q^n} für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n \in \mathbb{N}} ). Die geometrische Reihe ist also:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S = \sum_{n=0}^\infty q^n.}

Eine spezielle geometrische Reihe ist

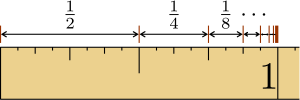
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S = \sum_{n=0}^\infty \frac{1}{2^n} = 1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\cdots}

Diese Schreibweise bezeichnet nach der oben gegebenen Darstellung den Grenzwert der Folge

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1,\ \frac{3}{2},\ \frac{7}{4},\ \frac{15}{8},\ \dotsc}

Man kann die Konvergenz dieser Reihe auf der Zahlengeraden visualisieren: Stellen wir uns eine Linie mit der Länge zwei vor, auf der aufeinanderfolgende Abschnitte mit den Längen 1, 1/2, 1/4 usw. markiert sind. Es gibt auf dieser Linie immer noch Platz für einen weiteren Abschnitt, da immer noch so viel Platz ist, wie der letzte Abschnitt lang war: Wenn wir die Strecke 1/2 markiert haben, haben wir insgesamt 3/2 verbraucht, es bleiben also noch 1/2 übrig. Wenn wir nun 1/4 wegstreichen, bleibt ein weiteres 1/4 übrig etc. Da das „Reststück“ beliebig klein wird, ist der Grenzwert gleich 2.

Konvergente geometrische Reihen sind auch ein Gegenstand der Paradoxa von Zenon.

Ein Beispiel für eine divergente Reihe mit mehreren Häufungspunkten ist die Summe über die Folge +1, −1, +1, −1, … Die Reihe wechselt zwischen den Werten 1 und 0 (die Folge hingegen wechselt zwischen 1 und −1).

Semantik

Dem Symbol

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{i=0}^\infty a_i}

kommen zwei unterschiedliche Bedeutungen zu, zwischen denen aus dem Kontext heraus entschieden werden muss. Einmal steht das Symbol für den Wert der Reihe, der im Fall konvergenter Reihen existiert oder im Fall divergenter Reihen nicht existiert:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{i=0}^\infty a_i = \lim_{N\to\infty} \sum_{i=0}^N a_i} .

Andererseits repräsentiert das Symbol die Reihe als Folge der Partialsummen, unabhängig vom Konvergenzverhalten:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{i=0}^\infty a_i = (a_0,a_0+a_1,a_0+a_1+a_2,a_0+a_1+a_2+a_3,...)} .

Fast immer ist mit dem Symbol der Grenzwert gemeint. Wenn man die Folge der Partialsummen meinen möchte, benutzt man Wendungen wie „…die Reihe, betrachtet als Folge ihrer Partialsummen,…“

Rechnen mit Reihen

Im Gegensatz zu gewöhnlichen (endlichen) Summen gelten für Reihen einige übliche Regeln der Addition nur bedingt. Man kann also nicht bzw. nur unter bestimmten Voraussetzungen mit ihnen wie mit endlichen Summenausdrücken rechnen.

Summen und Vielfache

Man kann konvergente Reihen gliedweise addieren, subtrahieren oder mit einem festen Faktor (aber nicht einer anderen Reihe) multiplizieren (vervielfachen). Die resultierenden Reihen sind ebenfalls konvergent, und ihr Grenzwert ist die Summe bzw. Differenz der Grenzwerte der Ausgangsreihen bzw. das Vielfache des Grenzwertes der Ausgangsreihe. D. h.

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{i=0}^\infty (a_i + b_i) = \sum_{i=0}^\infty a_i + \sum_{i=0}^\infty b_i}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{i=0}^\infty (a_i - b_i) = \sum_{i=0}^\infty a_i - \sum_{i=0}^\infty b_i}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{i=0}^\infty A\cdot a_i = A\cdot \sum_{i=0}^\infty a_i}

Produkte

Man kann absolut konvergente Reihen gliedweise miteinander multiplizieren. Die Produktreihe ist ebenfalls absolut konvergent und ihr Grenzwert ist das Produkt der Grenzwerte der Ausgangsreihen. D. h.

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{i, j=0}^\infty (a_i\cdot b_j) = \left(\sum_{i=0}^\infty a_i\right) \cdot \left( \sum_{j=0}^\infty b_j \right)}

Da die Schreibweise (auf der linken Seite der Gleichung) der Produktreihe mit zwei Indizes in bestimmten Zusammenhängen „unhandlich“ ist, wird die Produktreihe auch in Form des Cauchyprodukts geschrieben. Der Name ergibt sich daraus, dass die Glieder der Produktreihe mit Hilfe des cauchyschen Diagonalverfahrens gebildet werden, dabei werden die Glieder der Ausgangsfolgen in einem quadratischen Schema paarweise angeordnet, und die (durchnummerierten) Diagonalen dieses Schemas bilden die Produktglieder. Für die Produktreihe braucht man dann nur noch einen einzelnen Index. Die Produktreihe hat dann die folgende Form:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{i, j=0}^\infty (a_i\cdot b_j) = \sum_{n=0}^\infty (a_0\cdot b_n + a_1\cdot b_{n-1} + \dotsb + a_{n-1}\cdot b_1 + a_n\cdot b_0) = \sum_{n=0}^\infty \left(\sum_{m=0}^n a_m\cdot b_{n-m}\right)}

Rechnen innerhalb der Reihe

Klammerung (Assoziativität)

Man kann innerhalb einer konvergenten Reihe die Glieder beliebig durch Klammern zusammenfassen. Man kann also beliebig viele Klammern in den „unendlichen Summenausdruck“ einfügen, man darf sie nur nicht innerhalb eines (aus mehreren Termen zusammengesetzten) Gliedes setzen. Der Wert der Reihe ändert sich durch die zusätzlich eingefügte Klammerung dann nicht.

Dies gilt für divergente Reihen im Allgemeinen nicht, was man leicht am folgenden Beispiel erkennt.

Die Reihe

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{i=0}^\infty (-1)^i = 1 - 1 + 1 - 1 + \dotsb }

divergiert, während die beklammerte Reihe

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{i=0}^\infty ((-1)^{2i} + (-1)^{2i+1}) = (1 - 1) + (1 - 1) + \dotsb = 0 + 0 + \dotsb = 0 }

gegen Null konvergiert und die anders beklammerte Reihe

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1 + \sum_{i=1}^\infty ((-1)^{2i-1} + (-1)^{2i}) = 1 + (-1 + 1) + (-1 + 1) + \dotsb = 1+ 0 + 0 + \dotsb = 1 }

gegen noch eine andere Zahl konvergiert.

Andererseits kann man aber keine Klammern ohne Weiteres weglassen. Man kann das aber immer dann, wenn die resultierende Reihe wieder konvergent ist. In diesem Falle bleibt auch der Reihenwert unverändert. Falls die „minderbeklammerte“ Reihe nämlich konvergent ist, kann man ihr dieselben Klammern wieder hinzufügen, die man zuvor weggenommen hat, und die Gleichheit des Grenzwertes ergibt sich nach dem oben Gesagten, wenn man darin die Rollen vertauscht und die „minderbeklammerte“ Reihe nun als Reihe betrachtet, der man Klammern hinzufügt.

Umordnung (Kommutativität)

→ Hauptartikel: Umordnung von Reihen

Eine Umordnung einer Reihe wird durch eine Permutation ihrer Indexmenge dargestellt. Ist die Indexmenge zum Beispiel (wie meist) die Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \N} der natürlichen Zahlen und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma\colon\N\rightarrow\N,\ i\mapsto \sigma(i)} , eine bijektive Abbildung der natürlichen Zahlen auf sich, so heißt

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{i=0}^\infty a_{\sigma(i)}}

eine Umordnung der Reihe

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{i=0}^\infty a_i.}

Man kann konvergente Reihen unter Beibehaltung ihres Wertes dann und nur dann beliebig umordnen, wenn sie unbedingt bzw. absolut konvergent sind. Es gilt für unbedingt (oder absolut) konvergente Reihen:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{i=0}^\infty a_i = \sum_{i=0}^\infty a_{\sigma(i)}} für alle bijektiven Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma\colon \N \to \N} .

Bedingt konvergente Reihen dürfen nur endlich umgeordnet werden, d. h. ab einem gewissen Index muss für die Umordnung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma(i) = i} gelten.

Absolute und unbedingte Konvergenz

Eine Reihe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{n=0}^\infty a_n} heißt absolut konvergent, wenn die Reihe ihrer Absolutglieder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{n=0}^\infty \left|a_n\right|} konvergiert.

Eine konvergente Reihe wird formal als unbedingt konvergent definiert, wenn jede ihrer Umordnungen wieder konvergiert und denselben Grenzwert hat. Die letzte Eigenschaft braucht jedoch nicht vorausgesetzt zu werden, da jede Reihe, deren sämtliche Umordnungen konvergent sind, auch für jede Umordnung denselben Wert hat. Eine konvergente Reihe, die nicht unbedingt konvergent ist, heißt bedingt konvergent.

In endlich-dimensionalen Räumen gilt der Satz:

Eine Reihe ist genau dann unbedingt konvergent, wenn sie absolut konvergent ist.

Für eine bedingt konvergente Reihe kann man eine beliebige Zahl vorgeben und dann eine Umordnung dieser Reihe finden, die gegen genau diese Zahl konvergiert (riemannscher Umordnungssatz). Insbesondere kann man als Zahl auch keine Zahl vorgeben, soll heißen, dass die Reihe divergieren solle, und findet eine geeignete Umordnung, die das tut.

Konvergenzkriterien

Entscheidungsbaum zur Bestimmung des Konvergenzverhaltens von Reihen

→ Hauptartikel: Konvergenzkriterium

Im Folgenden seien die Zahlen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_n} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_n} stets reelle oder komplexe Zahlen, und die Reihe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S} sei definiert als

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S = \sum_{n=0}^\infty a_n.}

Zum Beweis der Konvergenz dieser Reihe gibt es diverse Konvergenzkriterien, die teils die bedingte, teils die stärkere absolute Konvergenz (Konvergenz der Reihe der Beträge der Glieder) zeigen:

Nullfolgenkriterium

Wenn die Reihe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S} konvergiert, dann konvergiert die Folge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (a_n)} der Summanden für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n \rightarrow \infty} gegen 0. Kontraponiert: Ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (a_n)} keine Nullfolge, so divergiert die entsprechende Reihe.
Die Umkehrung ist nicht allgemeingültig (ein Gegenbeispiel ist die harmonische Reihe).

Majorantenkriterium

Wenn alle Glieder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_n} der Reihe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S} nichtnegative reelle Zahlen sind, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S} konvergiert und für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_n\geq |b_n|}

gilt, dann konvergiert auch die Reihe

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T = \sum_{n=0}^\infty b_n}

absolut, und es ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |T|\le S} .

Minorantenkriterium

Wenn alle Glieder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_n} der Reihe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S} nichtnegative reelle Zahlen sind, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S} divergiert und für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_n\leq b_n}

mit nichtnegativen reellen Zahlen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_n} gilt, dann divergiert auch die Reihe

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{n=0}^\infty b_n} .

Quotientenkriterium

Wenn eine Konstante Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C\in [0, 1)} und ein Index Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N} existieren, sodass für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n\ge N} gilt

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left| \frac{a_{n+1}}{a_n} \right| \le C,}

dann konvergiert die Reihe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S} absolut.

Wurzelkriterium

Wenn eine Konstante Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C\in [0, 1)} und ein Index Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N} existieren, sodass für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n\ge N} gilt

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sqrt[n]{|a_n|} \le C,}

dann konvergiert die Reihe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S} absolut.

Integralkriterium

Ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f\colon [1, \infty) \to [0, \infty)} eine monoton fallende Funktion mit

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(n)=a_n} für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} ,

dann konvergiert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S} genau dann, wenn das Integral

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_1^\infty f(x)\,\mathrm dx}

existiert.

Leibniz-Kriterium

Eine Reihe der Form

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S = \sum_{n=0}^\infty (-1)^n a_n}

mit nichtnegativen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_n} wird alternierende Reihe genannt. Eine solche Reihe konvergiert, wenn die Folge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_n} monoton gegen 0 konvergiert. Die Umkehrung ist nicht allgemeingültig.

Beispiele

• Eine geometrische Reihe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{n=0}^\infty z^n} konvergiert genau dann, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |z|<1} .
• Die Dirichletreihe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{n=1}^\infty\frac1{n^r}} konvergiert für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r>1} und divergiert für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r\le1} , was mit dem Integralkriterium gezeigt werden kann. Als Funktion von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r} aufgefasst, ergibt diese Reihe die Riemannsche Zetafunktion.
• Die Teleskopreihe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{n=1}^\infty (b_n-b_{n+1})} konvergiert genau dann, wenn die Folge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (b_n)_{n \in \N}} gegen eine Zahl Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} konvergiert. Der Wert der Reihe ist dann Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_1-L} .

Anwendungen

Darstellung mathematischer Konstanten

Neben der Konvergenz und dem numerischen Wert einer Reihe ist auch der symbolische Wert einer Reihe von Bedeutung. Beispielsweise lassen sich so mathematische Konstanten darstellen und numerisch berechnen. Beispiel für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ln2} (natürlicher Logarithmus)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ln2 = \sum_{k=1}^{\infty}\frac1{k2^k} \quad \text{oder} \quad \ln2 = \tfrac23\sum_{k=0}^{\infty}\frac1{(2k+1)9^k} \,. }

Für wichtige Reihendarstellungen existieren Tabellierungen in Reihentafeln.

Reihen von Funktionen

Anstatt Folgen von Zahlen kann man auch Folgen von Funktionen betrachten und entsprechend Reihen definieren. Hier kommt zur Frage der Konvergenz noch die nach den Eigenschaften der Grenzfunktion hinzu. Umgekehrt kann man fragen, durch welche Reihe sich eine Funktion darstellen lässt. So eine Darstellung nennt sich Reihenentwicklung.

Potenzreihen

Einige wichtige Funktionen können als Taylorreihen dargestellt werden. Diese sind bestimmte unendliche Reihen, in denen Potenzen einer unabhängigen Variable vorkommen. Solche Reihen werden allgemein Potenzreihen genannt. Werden auch negative Potenzen der Variablen zugelassen, spricht man von Laurentreihen.

Fourierreihen

Als Fourierreihe einer Funktion bezeichnet man ihre Entwicklung nach trigonometrischen Funktionen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sin (nx)} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \cos (nx)} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (n = 0, 1, 2, 3, \dots)} . Die Eulersche Reihe ist ebenfalls von diesem Typ.

Dirichletreihen

Als Dirichletreihe bezeichnet man eine Entwicklung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F(s)=\sum_{n=1}^{\infty} \frac{f(n)}{n^s},} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s=\sigma+it \in \mathbb{C}.}

Ein wichtiges Beispiel ist die Reihendarstellung der Riemannschen Zetafunktion

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \zeta(s)=\sum_{n=1}^{\infty} \frac1{n^s},} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \operatorname{Re}\,s>1} .

Präfixsumme

In der Informatik wird mit Präfixsumme ein Algorithmus bezeichnet, der jeden Eintrag Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_k} eines Arrays durch die Partialsumme Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_k} ersetzt. Die Präfixsumme kann parallelisiert werden und ist daher ein grundlegender Algorithmus für Rechnersysteme mit mehreren Prozessorkernen, GPUs oder Rechnerclustern.

Weblinks

Wikibooks: Mathe für Nicht-Freaks: Reihe – Lern- und Lehrmaterialien

Wikibooks: Mathe für Nicht-Freaks: Konvergenz einer Reihe – Lern- und Lehrmaterialien

Literatur

• Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage. Springer, Berlin u. a. 1996, ISBN 3-540-59111-7, Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen 2).
• Izrail Solomonovic Gradshteyn, Iosif Mojseevic Ryzhik: Table of Integrals, Series and Products. Herausgegeben von Alan Jeffrey und Daniel Zwillinger. 7. Ausgabe. Elsevier Academic Press, Amsterdam u. a. 2007, ISBN 978-0-12-373637-6.