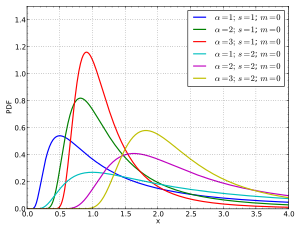
Fréchet-Verteilung
Die Fréchet-Verteilung ist eine absolutstetige Verteilung über den positiven reellen Zahlen, die einen echt positiven reellen Skalierparameter Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} nutzt. Benannt ist sie nach dem französischen Mathematiker Maurice René Fréchet.
Verteilungs und Dichtefunktion
Die Fréchet-Verteilung besitzt für einen reellen Parameter Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}} >0 die Verteilungsfunktion
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\Phi}_{\alpha}(x) = \exp(-x^{-\alpha}) = \exp(-1/ x{^\alpha} )}
Die dazugehörige Dichtefunktion ist
Momente und Median
Im Folgenden sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} eine Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} -Fréchet-verteilten Zufallsvariable und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Gamma\left(x\right)} die Gamma-Funktion.
Median
Der Median ist
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \operatorname{Med}(X) = \left(\frac{1}{\log_e(2)}\right)^{1/\alpha}}
Existenz von Momenten
Die k-ten Momente der Fréchet-Verteilung existieren genau dann, wenn .
Erwartungswert
Der Erwartungswert ist
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \operatorname{E}(X) = \Gamma\left(1-\frac{1}{\alpha}\right)} .
Varianz
Die Varianz ist
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \operatorname{Var}(X) = \Gamma\left(1-\frac{2}{\alpha}\right)- \left(\Gamma\left(1-\frac{1}{\alpha}\right)\right)^2}
Schiefe
Die Schiefe ist
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma_m(X) = \frac{\Gamma\left(1-\frac {3}{\alpha}\right)-3\Gamma\left(1-\frac {2}{\alpha}\right)\Gamma\left(1-\frac {1}{\alpha}\right)+2\Gamma^3\left(1-\frac {1}{\alpha} \right)}{\left( \Gamma\left(1-\frac{2}{\alpha}\right)-\Gamma^2\left(1-\frac{1}{\alpha}\right) \right)^{\frac{3}{2}} } }
Kurtosis
Die Kurtosis ist
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \operatorname{Kurt}(X) = -6+ \frac{\Gamma \left(1-\frac{4}{\alpha}\right) -4\Gamma\left(1-\frac{3}{\alpha}\right) \Gamma\left(1-\frac{1}{\alpha}\right)+3 \Gamma^2\left(1-\frac{2}{\alpha} \right)} {\left[\Gamma \left(1-\frac{2}{\alpha}\right) - \Gamma^2 \left(1-\frac{1}{\alpha}\right) \right]^2} }
Zusammenhang mit anderen Verteilungen
Ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} Fréchet-verteilt mit Parameter , so ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ln X} Gumbel-verteilt mit Parametern Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu=0} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta=\frac{1}{\alpha}} .
Nach dem Theorem von Fisher-Tippett kann eine standardisierte, nicht-degenerierte Extremwertverteilung nur gegen eine der drei generalisierten Extremwertverteilungen (GEV) konvergieren, von denen eine die Fréchet-Verteilung ist.
Anwendung
Sie ist daher eine wichtige Verteilung zur Bestimmung von Risiken in der Finanzstatistik, wie zum Beispiel des Value at Risk und des Expected Shortfall.
Literatur
- J. Franke, W. Härdle, C. M. Hafner: Statistics of Financial Markets: An Introduction. 2. Auflage. Springer, Berlin/ Heidelberg/ New York 2008, ISBN 978-3-540-76269-0.
- J. Franke, C. M. Hafner, W. Härdle: Einführung in die Statistik der Finanzmärkte. 2. Auflage. Springer, Berlin/ Heidelberg/ New York 2004, ISBN 3-540-40558-5.
Einzelnachweise
- mathematik.uni-kl.de – Jean-Pierre-Stockis, Fachbereich Mathematik der TU Kaiserslautern, Financial Statistics, Part II, abgerufen am 4. Januar 2011