Dies ist die
aktuelle Version dieser Seite, zuletzt bearbeitet am 30. Juli 2021 um 17:20 Uhr durch
imported>Himuralibima(45940) .
(Unterschied) ← Nächstältere Version | Aktuelle Version (Unterschied) | Nächstjüngere Version → (Unterschied)
Die Dreiecksverteilung (oder Simpsonverteilung , nach Thomas Simpson ) ist eine stetige Wahrscheinlichkeitsverteilung , die in der Wahrscheinlichkeitstheorie und Statistik verwendet wird.
Definition Die Dreiecksverteilung ist definiert durch die auf dem Intervall
[
a
,
b
]
{\displaystyle \left[a,b\right]}
Wahrscheinlichkeitsdichtefunktion
f
(
x
)
=
{
2
(
x
−
a
)
(
b
−
a
)
(
c
−
a
)
,
wenn
a
≤
x
<
c
2
b
−
a
,
wenn
x
=
c
2
(
b
−
x
)
(
b
−
a
)
(
b
−
c
)
,
wenn
c
<
x
≤
b
.
{\displaystyle f(x)={\begin{cases}{\frac {2(x-a)}{(b-a)(c-a)}},&{\text{wenn }}a\leq x<c\\{\frac {2}{b-a}},&{\text{wenn }}x=c\\{\frac {2(b-x)}{(b-a)(b-c)}},&{\text{wenn }}c<x\leq b.\end{cases}}}
Hierbei bestimmen die Parameter
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
a
<
b
{\displaystyle a<b}
a
≤
c
≤
b
{\displaystyle a\leq c\leq b}
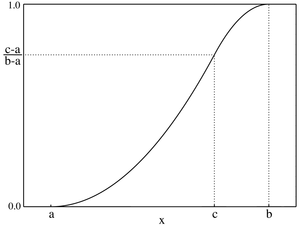
Graph der Dichtefunktion sieht wie ein Dreieck aus und gibt dieser Verteilung ihren Namen. Die
y
{\displaystyle y}
x
∈
[
a
,
b
]
{\displaystyle x\in \left[a,b\right]}
Eigenschaften Verteilungsfunktion Die Verteilungsfunktion ist
F
(
x
)
=
{
(
x
−
a
)
2
(
b
−
a
)
(
c
−
a
)
,
wenn
a
≤
x
<
c
c
−
a
b
−
a
,
wenn
x
=
c
1
−
(
b
−
x
)
2
(
b
−
a
)
(
b
−
c
)
,
wenn
c
<
x
≤
b
.
{\displaystyle F(x)={\begin{cases}{\frac {(x-a)^{2}}{(b-a)(c-a)}},&{\text{wenn }}a\leq x<c\\{\frac {c-a}{b-a}},&{\text{wenn }}x=c\\1-{\frac {(b-x)^{2}}{(b-a)(b-c)}},&{\text{wenn }}c<x\leq b.\end{cases}}}
Die Umkehrfunktion der Verteilungsfunktion lautet
F
−
1
(
y
)
=
{
a
+
y
(
b
−
a
)
(
c
−
a
)
,
wenn
0
≤
y
≤
(
c
−
a
)
(
b
−
a
)
b
−
(
b
−
a
)
(
b
−
c
)
(
1
−
y
)
,
wenn
(
c
−
a
)
(
b
−
a
)
≤
y
≤
1
{\displaystyle F^{-1}(y)={\begin{cases}a+{\sqrt {y(b-a)(c-a)}},&{\text{wenn }}0\leq y\leq {\frac {(c-a)}{(b-a)}}\\b-{\sqrt {(b-a)(b-c)}}{\sqrt {(1-y)}},&{\text{wenn }}{\frac {(c-a)}{(b-a)}}\leq y\leq 1\end{cases}}}
Erwartungswert und Median Der Erwartungswert einer dreiecksverteilten Zufallsvariable
X
{\displaystyle X}
E
(
X
)
=
a
+
b
+
c
3
.
{\displaystyle \operatorname {E} (X)={\frac {a+b+c}{3}}.}
Für
b
−
c
>
c
−
a
{\displaystyle b-c>c-a}
Median
m
{\displaystyle m}
m
=
b
−
(
b
−
a
)
(
b
−
c
)
/
2
{\displaystyle m=b-{\sqrt {(b-a)(b-c)/2}}}
Pearson .Varianz Die Varianz einer dreiecksverteilten Zufallsvariable
X
{\displaystyle X}
Var
(
X
)
=
a
2
+
b
2
+
c
2
−
a
b
−
a
c
−
b
c
18
=
(
a
−
b
)
2
+
(
b
−
c
)
2
+
(
a
−
c
)
2
36
.
{\displaystyle \operatorname {Var} (X)={\frac {a^{2}+b^{2}+c^{2}-ab-ac-bc}{18}}={\frac {(a-b)^{2}+(b-c)^{2}+(a-c)^{2}}{36}}.}
Beziehung zu anderen Verteilungen Summe gleichverteilter Zufallsgrößen Die Summe zweier identischer unabhängiger und stetig gleichverteilter Zufallsvariablen ist dreiecksverteilt mit
b
−
c
=
c
−
a
{\displaystyle b-c=c-a}
Standardabweichung
6
(
b
−
a
)
/
12
≈
0,204
(
b
−
a
)
{\displaystyle {\sqrt {6}}(b-a)/12\approx 0{,}204(b-a)}
mittlerer absoluter Abweichung
(
b
−
a
)
/
6
≈
0,167
(
b
−
a
)
{\displaystyle (b-a)/6\approx 0{,}167(b-a)}
Interquartilsabstand
(
1
−
2
/
2
)
(
b
−
a
)
≈
0,293
(
b
−
a
)
{\displaystyle (1-{\sqrt {2}}/2)(b-a)\approx 0{,}293(b-a)}
Betrag der Differenz gleichverteilter Zufallsgrößen Der Betrag der Differenz zweier identischer unabhängiger und stetig gleichverteilter Zufallsvariablen
|
X
1
−
X
2
|
{\displaystyle |X_{1}-X_{2}|}
a
=
c
=
0
{\displaystyle a=c=0}
Trapezverteilung Die Dreiecksverteilung ist ein Spezialfall der Trapezverteilung .
Diskrete Dreiecksverteilung Die stetige Dreiecksverteilung kann als Grenzwert einer diskreten Dreiecksverteilung aufgefasst werden.
Literatur Weblinks
Diskrete univariate Verteilungen
Kontinuierliche univariate Verteilungen
Multivariate Verteilungen
![{\displaystyle \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa)







![{\displaystyle x\in \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c4dd3adabf0430c82fd37cb45576a1df8c60002)