Kontinuumsmechanik

Kontinuumsmechanik ist ein Teilgebiet der Mechanik, das die Bewegung von deformierbaren Körpern als Antwort auf äußere Belastungen studiert. Der Begriff Deformation wird hier so weit gefasst, dass auch das Fließen einer Flüssigkeit oder das Strömen eines Gases darunter fällt. Entsprechend gehören Festkörpermechanik, Strömungsmechanik und Gastheorie zur Kontinuumsmechanik. In der Kontinuumsmechanik wird vom mikroskopischen Aufbau der Materie, also zum Beispiel der Gitterstruktur kristalliner Festkörper und der molekularen Struktur von Flüssigkeiten, abgesehen und der Untersuchungsgegenstand als ein Kontinuum genähert. Die Größen Dichte, Temperatur und die drei Komponenten der Geschwindigkeit liegen an jedem Raumpunkt innerhalb eines Körpers vor, was die Kontinuumsmechanik zu einer Feldtheorie macht. Zu den nicht klassischen Theorien der Kontinuumsmechanik gehören die relativistische Kontinuumsmechanik, das Cosserat-Kontinuum, in dem jeder materielle Punkt zusätzlich drei Rotationsfreiheitsgrade besitzt oder die nicht lokalen Materialien.

Der theoretische Hintergrund der Kontinuumsmechanik liegt in der Physik, die praktische Anwendung erfolgt in verschiedenen Bereichen des Maschinenbaus, des theoretischen Bauingenieurwesens, der Werkstoffkunde, der Medizinischen Informatik sowie in der Geophysik und anderen Bereichen der Geowissenschaften. Insbesondere Anwendungen der beiden erstgenannten Bereiche werden als Technische Mechanik zusammengefasst.

Das im Bereich wissenschaftlich technischer Aufgabenstellungen der Festkörpermechanik bekannteste und am meisten angewandte numerische Berechnungsverfahren, die Finite-Elemente-Methode, löst die Gleichungen der Kontinuumsmechanik (näherungsweise) mit Methoden der Variationsrechnung. In der Strömungsmechanik kommt ein gleicher Rang dem Finite-Volumen-Verfahren zu.

Geschichte

Die Kontinuumsmechanik basiert auf der Mechanik, Physik, Differentialgeometrie, Differential- und Integralrechnung deren historischer Werdegang dort nachgeschlagen werden kann. Auch manche Etappen in der Entwicklung der Strömungsmechanik verlaufen mit der der Kontinuumsmechanik parallel. An dieser Stelle soll die spezifisch kontinuumsmechanische Entwicklung mit Betonung auf der Mechanik fester Körper skizziert werden.

Bereits Archimedes (287–212 v. Chr.) befasste sich mit grundlegenden mechanischen Fragestellungen, die Festkörper und Fluide betrafen, über 1500 Jahre bevor Leonardo da Vinci (1452–1519) Lösungen zahlreicher mechanischer Probleme ersann.

Galileo Galilei (1564–1642) diskutierte in seinen Discorsi Festigkeitsprobleme und begründete so die Festigkeitslehre in einer Zeit, als feste Körper zumeist als undeformierbar modelliert wurden. Edme Mariotte (1620–1684) lieferte Beiträge zu Problemen der Flüssigkeiten und Gase und stellte dabei erste Konstitutivgesetze auf, was Robert Hooke (1635–1703) mit dem nach ihm benannten Hooke’sche Gesetz 1676 auch für elastische Festkörper tat.

Isaac Newton (1643–1727) veröffentlichte 1686 seine Principia mit den Gravitations- und Bewegungsgesetzen. Die Mitglieder der Familie Bernoulli lieferten Beiträge zur Mathematik, Strömungsmechanik und – durch Jakob I Bernoulli (1654–1705) – zur Balkentheorie. Leonhard Euler (1707–1783) gab wesentliche Impulse zur Mechanik starrer und deformierbarer Körper sowie zur Hydromechanik. Jean-Baptiste le Rond d’Alembert (1717–1783) führte die eulersche Betrachtungsweise ein, leitete die lokale Massenbilanz her und formulierte das d’Alembertsche Prinzip. Joseph-Louis Lagrange (1736–1813) richtete 1788 in seinem grundlegenden Werk Mécanique analytique die Mechanik konsequent mathematisch aus.

Die in der Kontinuumsmechanik fundamentalen Begriffe des Spannungs- und Verzerrungstensors wurden von Augustin-Louis Cauchy (1789–1857) eingeführt. Weitere grundlegende Erkenntnisse wurden unter anderem von Siméon Denis Poisson (1781–1840), Claude Louis Marie Henri Navier (1785–1836), Gabrio Piola (1794–1850) und Gustav Robert Kirchhoff (1824–1887) eingebracht.

Aus industriellen und praktischen Bedürfnissen heraus dominierten im weiteren Verlauf technische Fragestellungen die Wissenschaft, die in Frankreich unter anderem in der von Cauchy, Poisson und Navier geprägten École polytechnique betrieben wurde. Deren Modell breitete sich in ganz Europa aus, in Deutschland als Technische Hochschule. Ingenieursdisziplinen wie Plastizitätstheorie, Kriechtheorie, Festigkeitslehre, Elastizitätstheorie und das Bauingenieurwesen entstanden. Als Folge dieser Aufsplitterung entwickelten sich Forschung und Lehre in den Teilgebieten unabhängig voneinander und gingen die kontinuumsmechanischen Zusammenhänge verloren. Auch die Strömungsmechanik entwickelte sich eigenständig.

Einen neuen Denkimpuls gab David Hilbert (1862–1943) mit seiner 1900 aufgestellten Liste von 23 mathematischen Problemen, die einer Lösung harren. Das sechste Problem „Wie kann die Physik axiomatisiert werden?“ ist zwar noch Anfang des 21. Jahrhunderts ungelöst, aber es entstanden noch vor dem Zweiten Weltkrieg fachübergreifende Arbeiten zur Kontinuumsmechanik insbesondere von Georg Hamel (1877–1954). Nach dem Krieg setzte eine intensive interdisziplinäre Grundlagenforschung ein, in der Clifford Truesdell (1919–2000) und Walter Noll (1925–2017) Impulse setzten.

Ab Mitte des 20. Jahrhunderts entwickelten sich die Computerhard- und software und die numerischen Verfahren zur Gleichungslösung so weit, dass mit ihrer Hilfe Lösungen für komplexe, praktische, kontinuumsmechanische Probleme gefunden werden können.

Überblick

Die Kontinuumsmechanik enthält zwei unterschiedliche Kategorien von Aussagen:

1. allgemeine Aussagen, die für alle materiellen Körper gelten, und
2. individuelle Aussagen, die Materialeigenschaften modellieren.

Die allgemeinen Aussagen beschreiben die Kinematik, hier die Geometrie der Deformation eines Körpers, und die Naturgesetze, die das physikalische Verhalten der Materie bestimmen.

Die individuellen Aussagen über die Materialeigenschaften werden in der Materialtheorie getroffen und schaffen die Verbindung zwischen den Naturgesetzen und den Deformationen von Körpern.

Die mathematische Beschreibung erlaubt die kompakte Formulierung der Naturgesetze in Bilanzgleichungen und der Materialeigenschaften in konstitutiven Gleichungen. Das System aus

1. kinematischen Gleichungen,
2. Bilanzgleichungen und
3. konstitutiven Gleichungen

ist abgeschlossen und führt zur prinzipiellen Vorhersagbarkeit der Reaktion von Körpern auf äußere Einwirkungen.

Kinematik

In der Kontinuumsmechanik ist es die Aufgabe der Kinematik, ein Maß für die Verzerrungen eines Körpers in Abhängigkeit von seiner Bewegung – inklusive Deformationen – zu definieren. Die Bewegung kann dabei von einem festen Raumpunkt oder von einem Partikel des Körpers aus beobachtet werden. Ersteres ist die Eulersche Betrachtungsweise, die die Strömungsmechanik benutzt, und letzteres die Lagrangesche Betrachtungsweise, die in der Festkörpermechanik bevorzugt wird.

Nun ist plausibel, dass wenn sich zwei im undeformierten Ausgangszustand benachbarte Partikel eines Körpers stark unterschiedlich bewegen, der Körper dort auch stark deformiert wird. Werden nun die in drei Raumrichtungen messenden Positionsdifferenzen der Partikel im deformierten Körper in Beziehung gesetzt zu ihren drei Positionsdifferenzen im undeformierten Ausgangszustand, entsteht bei kleiner werdenden Abständen der Partikel der Deformationsgradient, der ein lokales Maß für die Deformation des Körpers ist. Der Deformationsgradient kann in eine Drehung und rotationsfreie Streckung zerlegt werden, aus der sich die gesuchten Verzerrungsmaße ableiten.

Lineare Abbildung eines Vektors Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{v}} durch einen Tensor T

Der Deformationsgradient ist wie die Streckung und die Verzerrungsmaße ein Tensor zweiter Stufe. Diese Tensoren dienen hier der linearen Abbildung von geometrischen Vektoren, die im Allgemeinen dabei gedreht und gestreckt werden, siehe Abbildung rechts. Die Tensorrechnung kann nicht als allgemein bekannt vorausgesetzt werden, weshalb jedes Lehrbuch der Kontinuumsmechanik auch eine Einführung in die Tensorrechnung beinhaltet.

Naturgesetze

Bei der Übertragung des materiellen Körpers in einen mathematischen Raum wird der Körper homogenisiert, indem die auf Atome verteilte Materie durch ein Kontinuum ersetzt wird, was namensgebend für diese Wissenschaft ist. Durch diese Idealisierung erhält jeder Punkt des Körpers physikalische Eigenschaften wie Geschwindigkeit, Dichte und Temperatur.

Das zweite Newton’sche Gesetz beschreibt die Reaktion eines Körpers auf eine äußere Kraft. In der Realität und der Kontinuumsmechanik werden solche Kräfte immer flächig eingeleitet, die sich im Körper als Spannungen (mit der Dimension Kraft pro Fläche) fortpflanzen. Nun kann der Körper gedanklich zerschnitten werden, so dass sich an den Schnittflächen Schnittspannungen ausbilden, die jedoch von der Orientierung der Schnittflächen, d. h. ihren Normalenvektoren, abhängen. Nach dem Cauchy’schen Fundamentaltheorem stellen Spannungstensoren diese Abhängigkeit dar, indem sie die Normalen der Schnittflächen linear auf die Schnittspannungen abbilden. Der Spannungstensor ist grundlegend für die Formulierung der Naturgesetze in ihrer am materiellen Punkt gültigen Form.

Die Bilanzgleichungen der Mechanik beschreiben die Wirkung der Außenwelt auf einen Körper und die daraus resultierende Änderung physikalischer Größen. Diese Größen sind die Masse, der Impuls, der Drehimpuls und die Energie. Der zweite Hauptsatz der Thermodynamik wird in Form der Clausius-Duhem-Ungleichung berücksichtigt. Die in der Mechanik für ausgedehnte Körper formulierten Naturgesetze werden in der Kontinuumsmechanik als globale Integralgleichungen ausgedrückt, aus denen sich mit geeigneten Annahmen lokale Differentialgleichungen ableiten lassen, die an jedem Raumpunkt oder Partikel erfüllt sein müssen.

Die lokale Massenbilanz besagt, dass die Dichte am materiellen Punkt zeitlich konstant ist. Die lokale Impulsbilanz setzt die spezifische Impulsänderung in Beziehung zur spezifischen Schwerkraft und zum Antrieb durch einen Spannungsanstieg. Die Drehimpulsbilanz reduziert sich auf die Forderung nach der Symmetrie des Spannungstensors. Die Energiebilanz besagt, dass sich die innere Energie durch innere Wärmequellen, den spezifischen Wärmeeintrag und der spezifischen Spannungsleistung an Verzerrungsgeschwindigkeiten ändert. Bei isothermen Prozessen fordert die Clausius-Duhem-Ungleichung schließlich, dass die Produktion an Helmholtz’scher freier Energie die spezifische Spannungsleistung nicht überschreiten darf. Diese Bedingung ist weniger als Einschränkung physikalischer Prozesse, sondern vielmehr als Anforderung an Materialmodelle zu interpretieren: Es muss sichergestellt sein, dass die lokalen Formen der Clausius-Duhem-Ungleichung von den konstitutiven Gleichungen für beliebige Prozesse erfüllt werden.

Materialtheorie

Die mathematische Formulierung der Naturgesetze trifft keine Aussagen über die individuellen Eigenschaften der Körper – ob sie beispielsweise fest, flüssig oder gasförmig sind – und reicht daher nicht aus, die Bewegungen der Körper eindeutig zu bestimmen. Dazu bedarf es noch konstitutiver Gleichungen, die die materialspezifische Antwort des Körpers, z. B. auf eine äußere Kraft, beschreiben. In diesem Fall ist eine Beziehung zwischen den Deformationen des Körpers und den Reaktionskräften anzugeben. Die Materialtheorie beschäftigt sich mit diesen Beziehungen und wie sie in ein Materialmodell umgesetzt werden. Ziel eines Materialmodells ist es die wesentlichen Aspekte des Materialverhaltens zu beschreiben, wobei das was wesentlich ist, vom Beobachter festgelegt wird. Stoff- oder Materialgesetze, wie Materialmodelle manchmal genannt werden, haben nicht die allgemeine Gültigkeit physikalischer Gesetze.

Die klassische Kontinuumsmechanik betrachtet einfache Materialien, bei denen aus ihrer bisherigen Bewegung (Determinismus) das Verhalten an einem materiellen Punkt vollständig aus seiner Umgebung (Lokalität) bestimmt ist, und das unabhängig vom Bewegungszustand des Beobachters (Objektivität). Einfache Materialien sind also deterministisch, lokal und objektiv. Ihre Eigenschaften lassen sich mit materiellen Zwangsbedingungen, materiellen Symmetrien und konstitutiven Gleichungen wiedergegeben. Materielle Zwangsbedingungen schränken die Deformationsmöglichkeiten eines Materials ein, wie es z. B. die Inkompressibilität tut. Materielle Symmetrien beschreiben die Richtungsabhängigkeit des Materials, wie sie z. B. bei Holz gegeben ist. Die konstitutiven Gleichungen stellen schließlich eine Relation zwischen den Dehnungen und den Spannungen her.

Die sechs Materialmodelle der klassischen Materialtheorie sind das ideale Gas, das Newton’sche Fluid, das Hooke’sche Gesetz, die Viskoelastizität, Plastizität und Viskoplastizität. Aus den ersten drei Modellen leiten sich die Euler-Gleichungen, die Navier-Stokes-Gleichungen bzw. die Navier-Cauchy-Gleichungen ab.

Tensorrechnung

[[Hilfe:Cache|Fehler beim Thumbnail-Erstellen]]:

Lineare Abbildung eines Vektors Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{v}} durch einen Tensor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{T}} .

Wichtigstes mathematisches Hilfsmittel der Kontinuumsmechanik ist die Tensorrechnung, deren Kenntnis nicht allgemein vorausgesetzt werden kann. Hier sollen nur die im vorliegenden Artikel benutzten Rechenregeln kurz vorgestellt werden.

Die in der Kontinuumsmechanik meist benutzten Tensoren sind Tensoren zweiter Stufe, die geometrische Vektoren aus dem dreidimensionalen euklidischen Vektorraum linear aufeinander abbilden. Dabei werden die Vektoren im Allgemeinen gedreht und gestreckt, siehe Abbildung rechts. Für diese Tensoren gilt die komponentenweise Darstellung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{T}=\sum_{i,j=1}^3 T^{ij} \vec{g}_i \otimes \vec{G}_j}

mit Komponenten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T^{ij}} des Tensors, die zu mit dem dyadischen Produkt "Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \otimes} " verknüpften Vektoren aus zwei Vektorraumbasen ${\vec {g}}_{1,2,3}$ bzw. ${\vec {G}}_{1,2,3}$ des angenommenen Vektorraums gehören. Von verschiedenen Basen wird bei der Beschreibung mit konvektiven Koordinaten Gebrauch gemacht. Hier genügt es die Basen ${\vec {G}}_{1,2,3}$ und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{g}_{1,2,3}} mit der Standardbasis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{e}_{1,2,3}} zu identifizieren, so dass jeder Tensor mit seiner Matrixrepräsentation gleichgesetzt werden kann:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{T} = \sum_{i,j=1}^3 T_{ij}\vec{e}_i\otimes\vec{e}_j = \begin{pmatrix} T_{11} & T_{12} & T_{13} \\ T_{21} & T_{22} & T_{23} \\ T_{31} & T_{32} & T_{33} \end{pmatrix}}

Gegeben sei ein weiterer Tensor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{S}} und ein Vektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{v}} für die die komponentenweisen Darstellungen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{S}=\sum_{i,j=1}^3 S_{ij}\vec{e}_i\otimes\vec{e}_j \quad\textsf{und}\quad \vec{v}=\sum_{i=1}^3 v_i\vec{e}_i }

gelten. Die im Artikel verwendeten Operationen sind wie folgt definiert:

Operator	Definition
Addition und Subtraktion	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{S}\pm\mathbf{T} := \sum_{i,j=1}^3 (S_{ij}\pm T_{ij})\vec{e}_i\otimes\vec{e}_j }
Multiplikation mit einem Skalar x	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x\; \mathbf{T} :=\sum_{i,j=1}^3 x T_{ij}\vec{e}_i\otimes\vec{e}_j }
Tensorprodukt	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{S} \cdot \mathbf{T} := \sum_{i,j,k=1}^3 (S_{ik} T_{kj})\vec{e}_i\otimes\vec{e}_j }
Transposition	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \mathbf{T}^\top :=& \sum_{i,j=1}^3 T_{ij}\vec{e}_j\otimes\vec{e}_i = \begin{pmatrix} T_{11} & T_{21} & T_{31} \\ T_{12} & T_{22} & T_{32} \\ T_{13} & T_{23} & T_{33} \end{pmatrix} \\ (\mathbf{S\cdot T})^\top=&\mathbf{T^\top\cdot S^\top} \end{align}}
Transformation eines Vektors mit dem Skalarprodukt "Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \cdot} " von Vektoren	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{T} \cdot \vec{v} := \sum_{i,j=1}^3 T_{ij}v_j\vec{e}_i \;,\quad \vec{v}\cdot\mathbf{T} = \mathbf{T}^\top\cdot\vec{v} }
Invertierung	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \mathbf{T}^{-1}:\quad\mathbf{T}^{-1}\cdot\mathbf{T} =& \mathbf{T\cdot T}^{-1} = \mathbf{1} \\ \left(\mathbf{T}^\top\right)^{-1}=&\left(\mathbf{T}^{-1}\right)^\top=\mathbf{T}^{\top-1} \end{align}}
Frobenius-Skalarprodukt	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{S}:\mathbf{T} := \sum_{i,j=1}^3 S_{ij} T_{ij} }

Darin ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{1}} der Einheitstensor.

Des Weiteren wird die Fréchet-Ableitung benötigt, die die Differentialrechnung auf Vektoren und Tensoren verallgemeinert. Die Fréchet-Ableitung einer Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f} nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} ist der beschränkte lineare Operator Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathcal{A}} , der – sofern er existiert – in allen Richtungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h} dem Gâteaux-Differential entspricht, also

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathcal{A}(h) = \left. \frac{\mathrm{d}}{\mathrm{d}s}f(x+sh)\right|_{s=0} = \lim_{s\rightarrow 0} \frac{f(x+sh) - f(x)}{s} \quad\forall\; h}

gilt. Darin ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s\in \mathbb{R},\; f\,,x} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h} skalar-, vektor- oder tensorwertig aber Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h} gleichartig. Dann wird auch

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathcal{A}=\frac{\mathrm{d} f}{\mathrm{d} x}}

geschrieben. Weitere Definitionen und Rechenregeln sind in der Formelsammlung Tensoralgebra und Formelsammlung Tensoranalysis aufgeführt.

Kinematik

→ Hauptartikel: Kinematik

Hier sollen nur die spezifisch kontinuumsmechanischen Aspekte beschrieben werden, mehr ist im Hauptartikel nachzuschlagen. Die Kinematik gibt in der Kontinuumsmechanik Transformationsgleichungen für Größen in der Ausgangskonfiguration in die entsprechenden Größen in der Momentankonfiguration und leitet daraus Verzerrungsmaße ab.

Der materielle Körper

→ Hauptartikel: Konfiguration (Mechanik)

Der materielle Körper als Träger der physikalischen Prozesse erfüllt gleichmäßig Teile des Raumes unserer Anschauung. In der Kontinuumsmechanik wird der Körper mittels Konfigurationen bijektiv in einen euklidischen Vektorraum Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbb{V}^3} abgebildet, wobei die Eigenschaften des Körpers kontinuierlich über den Raum verschmiert werden. Mithilfe dieser Idealisierung wird der Körper als Punkt-Menge beschrieben, in der Gradienten und Integrale gebildet werden können.

Daraus ergeben sich zwei Konsequenzen:

1. Es gibt eine Größenskala, unterhalb derer die Aussagen der Kontinuumsmechanik ihre Gültigkeit verlieren. Diese Größenskala liegt oberhalb der Abmessungen des Repräsentativen-Volumen-Elementes (RVE), aus identischen Kopien von welchem der materielle Körper aufgebaut gedacht wird. Das RVE eines Kristalls kann beispielsweise eine Elementarzelle sein.
2. Ein innerer Punkt des Körpers bleibt immer ein innerer Punkt, weswegen die Beschreibung der Ausbreitung von Rissen mit Aussagen der klassischen Kontinuumsmechanik nicht möglich ist. Mit der Reaktion von Körpern auf Risse und der Rissausbreitung beschäftigt sich die Bruchmechanik, die ihrerseits auf das Vorhandensein eines Risses angewiesen ist.

Für einen Körper werden folgende Konfigurationen benutzt:

1. Die Referenz- oder Bezugskonfiguration Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_{R}(P)} , die der Identifikation der materiellen Punkte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P} dient. Die Ausgangskonfiguration Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{X} = \kappa_{0}(P)} des Körpers zu einem gesetzten Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {t}_{0}} ist zeitlich fixiert und kann und soll als Referenzkonfiguration dienen. Weil diese Position einmal vom Körper eingenommen wurde, liefert diese Referenzkonfiguration ein Objekt unserer Anschauung.
2. Die Momentankonfiguration Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{x} = \kappa_{t}(P)} bildet den deformierten Körper zur Zeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} ab.

Die Verknüpfung dieser Konfigurationen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{lll} \vec{\chi}:=\kappa_t \circ \kappa_0^{-1}:& V\subset\mathbb{V}^3 &\rightarrow v\subset\mathbb{V}^3\\ & \vec{X}&\mapsto \vec{x}\end{array}}

heißt Bewegungsfunktion und soll so oft stetig differenzierbar sein, wie es im jeweiligen Kontext notwendig ist. Der Urbildraum Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V} wird mit dem vom Körper in der Referenzkonfiguration eingenommenen Volumen identifiziert und der Bildraum Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v} mit dem vom Körper in der Momentankonfiguration eingenommenen Volumen.

Materielle und räumliche Koordinaten

Die materiellen Koordinaten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{X}} eines materiellen Punktes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P} sind die Komponenten seines Ortsvektors in der Ausgangskonfiguration:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{X}=\kappa_{0}(P )\in V \subset \mathbb{V}^3\,.}

Die Momentankonfiguration gibt zu jedem Zeitpunkt die räumlichen Koordinaten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{x}} des materiellen Punktes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P} im Raum:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{x}=\kappa_{t}(P) =\kappa_{t}(\kappa_{0}^{-1}( \vec{X})) =: \vec{\chi}(\vec{X},t) \in v \subset \mathbb{V}^3\,.}

Die Bewegungsfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{\chi}(\vec{X},t)} beschreibt bei festgehaltenem Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{X}} die Bahnlinie eines materiellen Punktes durch den Raum. Wegen der Bijektivität kann die Bewegungsfunktion jederzeit invertiert werden:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{X}=\vec{\chi}^{-1}(\vec{x},t) \in V \subset \mathbb{V}^3\,.}

Bei festgehaltenem Raumpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{x}} liefert die Bewegungsfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{\chi}^{-1}(\vec{x},t)} die Streichlinie durch den Raumpunkt.

Wegen der Eineindeutigkeit der Konfigurationen bei der Beschreibung des materiellen Körpers können alle einem materiellen Punkt zugeordneten Größen (z. B. Dichte, Temperatur und Geschwindigkeit) in Abhängigkeit von seinen materiellen oder räumlichen Koordinaten beschrieben werden. Wenn nicht anders angegeben, werden Größen in der materiellen Betrachtungsweise mit Großbuchstaben oder dem Index Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {(\;)}_{0}} und solche der räumlichen mit Kleinbuchstaben bezeichnet.

Lagrange’sche Betrachtungsweise

→ Hauptartikel: Lagrangesche Betrachtungsweise

Soll die Bewegung eines materiellen Punktes beobachtet werden und welche physikalischen Bedingungen in ihm herrschen, liegt es nahe, die dem materiellen Punkt zugeordneten Größen in Abhängigkeit von den materiellen Koordinaten aufzuschreiben, denn diese sind für jeden materiellen Punkt konstant. So ergibt sich die materielle oder Lagrange’sche Betrachtungsweise (nach Joseph-Louis Lagrange), die in der Festkörpermechanik bevorzugt wird.

Euler’sche Betrachtungsweise

→ Hauptartikel: Eulersche Betrachtungsweise

Sollen andererseits die physikalischen Prozesse an einem festen Raumpunkt verfolgt werden, liegt es nahe, die physikalischen Größen in Abhängigkeit von den räumlichen Koordinaten zu notieren. Das ist die räumliche oder Euler’sche Betrachtungsweise, die in der Strömungsmechanik benutzt wird.

Differentialoperatoren

In der Kontinuumsmechanik werden für die materielle und die räumliche Betrachtungsweise vor allem zwei Differentialoperatoren, für den Gradienten und die Divergenz, gebraucht:

Feldvariable	Divergenz DIV	Gradient GRAD
Skalarfeld Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \phi}		Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial \phi}{\partial \vec{X}} =\sum_{i=1}^3\frac{\partial \phi}{\partial X_i}\vec{e}_i}
Vektorfeld Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{\phi}=\sum_{i=1}^3 \phi_i \vec{e}_i}	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{i=1}^3 \vec{e}_i\cdot\frac{\partial \vec{\phi}}{\partial X_i} =\sum_{i=1}^3\frac{\partial \phi_i}{\partial X_i}}	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial \vec{\phi}}{\partial \vec{X}} =\sum_{i,j=1}^3\frac{\partial \phi_i}{\partial X_j}\vec{e}_i \otimes\vec{e}_j }
Tensorfeld Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \boldsymbol{\phi}=\sum_{i,j=1}^3 \phi_{ij} \vec{e}_i\otimes \vec{e}_j}	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum_{i=1}^3\vec{e}_i\cdot\frac{\partial \boldsymbol{\phi}}{\partial X_i} =\sum_{i,j=1}^3\frac{\partial \phi_{ij}}{\partial X_i}\vec{e}_j}

Die materiellen Operatoren DIV und GRAD beinhalten die materiellen Ableitungen nach den materiellen Koordinaten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{X}} . Entsprechende Definitionen gelten für die räumlichen Operatoren div und grad in der räumlichen Formulierung, die die räumlichen Ableitungen nach den räumlichen Koordinaten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{x}} einschließen.

Lokale und materielle Zeitableitung

Die Zeitableitung einer einem materiellen Punkt zugeordneten Größe, z. B. der Temperatur Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T} , kann bei festgehaltenem Raumpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{x}} oder festgehaltenem materiellen Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{X}} ausgewertet werden. Ersteres ist die lokale Zeitableitung letzteres die materielle oder substantielle Ableitung. Weil sich die Naturgesetze auf materielle Punkte beziehen, ist die substantielle Zeitableitung physikalisch bestimmend.

Die partielle Ableitung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial}{\partial t}T(\vec{x},t)} bei festgehaltenem Raumpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{x}} ist die lokale Zeitableitung, d. h. die Änderungsrate die an einem festen Raumpunkt vorliegt.

Die materielle Zeitableitung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tfrac{\mathrm{D}}{\mathrm{D}t}} ist in der Lagrange’schen Betrachtungsweise die partielle Ableitung nach der Zeit

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{T}_{0}(\vec{X},t) :=\frac{\mathrm{D}}{\mathrm{D}t}T_{0} (\vec{X},t) :=\left.\frac{\mathrm{d}}{\mathrm{d}t}T_{0} (\vec{X},t)\right|_{\vec{X}\;\text{fest}} =\frac{\partial}{\partial t} T_{0} (\vec{X},t)}

und wird hier auch mit dem aufgesetzten Punkt gekennzeichnet. Die materielle Zeitableitung ist also die an einem Partikel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{X}} beobachtbare Änderungsrate einer Feldvariablen. In diesem Beispiel würde ein Thermometer fortlaufend die Temperaturänderungen nur dieses einen Partikels Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{X}} messen.

In der Euler’schen Betrachtungsweise setzt sich die materielle Zeitableitung aus dem lokalen und einem zusätzlichen konvektiven Anteil zusammen:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\mathrm{D}}{\mathrm{D}t}T(\vec{\chi}(\vec{X},t),t) =\frac{\partial}{\partial\vec{x}}T(\vec{x},t) \cdot\frac{\mathrm{D}}{\mathrm{D}t}\vec{\chi}(\vec{X},t) + \frac{\partial}{\partial t}T(\vec{x},t) =\operatorname{grad}\;(T(\vec{x},t)) \cdot\vec{v}(\vec{x},t) + \frac{\partial}{\partial t}T(\vec{x},t)}

Die materiellen Koordinaten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{X}=\vec{\chi}^{-1}(\vec{x},t)} gehören zu dem Partikel, das sich zur Zeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} am Ort Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{x}} befindet und zu diesem Zeitpunkt die Geschwindigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{v}(\vec{x},t)=\dot{\vec{\chi}}(\vec{X},t)} besitzt, und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \operatorname{grad}(T) \cdot\vec{v}} stellt den konvektiven Anteil dar. Ganz analog bildet sich die materielle Zeitableitung einer vektoriellen Größe, beispielsweise die substantielle Beschleunigung:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{\vec{v}}=\frac{\mathrm{D}}{\mathrm{D}t}\vec{v} =\frac{\partial}{\partial t}\vec v+\operatorname{grad}(\vec{v})\cdot\vec{v} =\frac{\partial}{\partial t}\vec{v}+(\vec{v}\cdot\nabla)\vec{v}\,.}

Letztere Schreibweise mit dem Nabla-Operator Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nabla} wird in der Strömungsmechanik bevorzugt.

Der Deformationsgradient

→ Hauptartikel: Deformationsgradient

Deformationsgradient

Der Deformationsgradient ist die grundlegende Größe zur Beschreibung von Verformungen, die sich aus lokalen Längenänderungen und von Winkeländerungen zwischen materiellen Linienelementen ergeben. Der Deformationsgradient transformiert die Tangentialvektoren an materielle Linien in der Ausgangskonfiguration in die Momentankonfiguration, siehe Bild. Berechnet wird der Deformationsgradient aus der Ableitung der Bewegungsfunktion nach den materiellen Koordinaten

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{F}(\vec{X},t) =\operatorname{GRAD}(\vec{\chi}(\vec{X},t)) =\frac{\mathrm{d}\chi_i(\vec{X},t)}{\mathrm{d}X_j}\vec{e}_i\otimes\vec{e}_j =\frac{\mathrm{d}\vec{x}}{\mathrm{d}\vec{X}} }

und kann auch mit der Richtungsableitung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{F}(\vec{X},t) \cdot \mathrm{d}\vec{X} =\left.\frac{\mathrm{d}}{\mathrm{d}s}\vec{\chi}{(\vec{X}+s\;\mathrm{d}\vec{X},t)} \right|_{s=0}=\mathrm{d}\vec{x}}

dargestellt werden, was seine Transformationseigenschaften der Linienelemente Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{d}\vec{X}} verdeutlicht.

Der Deformationsgradient transformiert auch das Oberflächenelement Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{N}\mathrm{d}A} , der mit dem Flächenstück Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{d} A} multiplizierten Normalen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{N}} des Flächenstücks, und das Volumenelement Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{d} V} von der Ausgangskonfiguration in die Momentankonfiguration:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{lcl} \vec{n}\mathrm{d}a &=& \det(\mathbf{F}){\mathbf{F}}^{\top-1} \cdot \vec{N}\mathrm{d}A \\ \mathrm{d}v&=&\det(\mathbf{F})\mathrm{d}V\end{array}\,.}

Der Operator Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \det(\;)} gibt die Determinante und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (\;)^{\top-1}} die transponiert Inverse. Mit diesen Elementen können Integrale in der Ausgangs- und der Momentankonfiguration (gleichbedeutend: in der materiellen und räumlichen Formulierung) ineinander umgerechnet werden.

Verzerrungstensoren

→ Hauptartikel: Verzerrungstensor

Veranschaulichung der Polarzerlegung

Mithilfe des Deformationsgradienten werden die Verzerrungsmaße definiert. Die Polarzerlegung des Deformationsgradienten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{F}=\mathbf{R \cdot U}=\mathbf{V \cdot R}} spaltet die Verformung lokal in eine reine Drehung, vermittelt durch den orthogonalen Rotationstensor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{R}} , und eine reine Streckung, vermittelt durch die symmetrischen positiv definiten rechten bzw. linken Strecktensor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{U}} bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{V}} , siehe Bild. Der räumliche Tensor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{V}} wird hier groß geschrieben, um eine Verwechselung mit der Geschwindigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{v}} zu vermeiden, die gelegentlich auch mit fetten Buchstaben geschrieben wird.

Die Strecktensoren dienen der Definition einer Vielzahl von Verzerrungstensoren, z. B. der Biot-Dehnungen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{E}_{N}=\mathbf{U}-\mathbf{1}\,,}

die gelegentlich Nominaldehnungen genannt werden, der Hencky Dehnungen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{E}_{H}=\ln(\mathbf{U})\,,}

(berechnet mittels Hauptachsentransformation von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{U}} , Bildung der Logarithmen der Diagonalelemente und Rücktransformation), der Green-Lagrange’schen Dehnungen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{E} =\tfrac{1}{2}(\mathbf{U\cdot U}-\mathbf{1}) =\tfrac{1}{2}({\mathbf{F}}^\top \cdot \mathbf{F}-\mathbf{1})}

und Euler-Almansi-Dehnungen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{e} =\tfrac{1}{2}(\mathbf{1}-\mathbf{V}^{-1} \cdot \mathbf{V}^{-1}) =\tfrac{1}{2}(\mathbf{1}-{\mathbf{F}}^{\top-1} \cdot \mathbf{F}^{-1}) \,.}

Wie oben steht Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{1}} für den Einheitstensor. Letztere Dehnungstensoren sind aus dem Vergleich zweier materieller Linienelemente Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{d}\vec{X}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{d}\vec{Y}} im Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{X}} motiviert:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rclcl} \mathrm{d}\vec{x}\cdot\mathrm{d}\vec{y} -\mathrm{d}\vec{X}\cdot\mathrm{d}\vec{Y} &=& (\mathbf{F} \cdot \mathrm{d}\vec{X})\cdot(\mathbf{F} \cdot \mathrm{d}\vec{Y}) -\mathrm{d}\vec{X}\cdot\mathrm{d}\vec{Y} &=& 2\mathrm{d}\vec{X}\cdot\mathbf{E} \cdot \mathrm{d}\vec{Y} \\ &=& \mathrm{d}\vec{x}\cdot\mathrm{d}\vec{y} -(\mathbf{F}^{-1} \cdot \mathrm{d}\vec{x})\cdot (\mathbf{F}^{-1} \cdot \mathrm{d}\vec{y}) &=& 2\mathrm{d}\vec{x}\cdot\mathbf{e} \cdot \mathrm{d}\vec{y}\end{array} }

Verzerrungsgeschwindigkeiten

Aus der materiellen Zeitableitung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{lclcl} \dfrac{\mathrm{D}}{\mathrm{D}t} ( \mathrm{d}\vec{x}\cdot\mathrm{d}\vec{y} -\mathrm{d}\vec{X}\cdot\mathrm{d}\vec{Y}) &=& \dfrac{\mathrm{D}}{\mathrm{D}t} [(\mathbf{F} \cdot \mathrm{d}\vec{X})\cdot(\mathbf{F} \cdot \mathrm{d}\vec{Y})] \\&=& (\dot{\mathbf{F}} \cdot \mathrm{d}\vec{X})\cdot (\mathbf{F} \cdot \mathrm{d}\vec{Y}) +(\mathbf{F} \cdot \mathrm{d}\vec{X})\cdot (\dot{\mathbf{F}} \cdot \mathrm{d}\vec{Y}) &=:& 2\mathrm{d}\vec{X}\cdot\dot{\mathbf{E}} \cdot \mathrm{d}\vec{Y} \\ &=& (\dot{\mathbf{F}} \cdot \mathbf{F}^{-1}\cdot\mathrm{d}\vec{x})\cdot\mathrm{d}\vec{y} +\mathrm{d}\vec{x}\cdot(\dot{\mathbf{F}} \cdot \mathbf{F}^{-1}\cdot\mathrm{d}\vec{y}) &=:& 2\mathrm{d}\vec{x}\cdot\mathbf{d} \cdot \mathrm{d}\vec{y} \end{array} }

leiten sich der materielle Verzerrungsgeschwindigkeitstensor

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{\mathbf{E}} =\frac{1}{2}(\dot{\mathbf{F}}^\top \cdot \mathbf{F} +\mathbf{F}^\top \cdot \dot{\mathbf{F}})}

und der räumliche

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{d}= \tfrac{1}{2}(\dot{\mathbf{F}} \cdot \mathbf{F}^{-1} +\mathbf{F}^{\top-1} \cdot \dot{\mathbf{F}}^\top)}

ab, die genau dann verschwinden, wenn Starrkörperbewegungen vorliegen.

Der räumliche Verzerrungsgeschwindigkeitstensor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{d}} ist der symmetrische Anteil des räumlichen Geschwindigkeitsgradienten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{l}} :

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{l} := \mathrm{grad}(\vec{v}(\vec{x},t)) = \frac{\mathrm{d}\vec{v}}{\mathrm{d}\vec{x}} = \frac{\mathrm{d}\dot{\vec{\chi}}}{\mathrm{d}\vec{X}} \cdot \frac{\mathrm{d}\vec{X}}{\mathrm{d}\vec{x}} = \dot{\mathbf{F}} \cdot \mathbf{F}^{-1} \quad\rightarrow\quad \mathbf{d} = \frac{1}{2}(\mathbf{l} + \mathbf{l}^\top )}

Geometrische Linearisierung

→ Hauptartikel: Geometrische Linearisierung

Vergleich verschiedener Dehnungsmasse bei der homogenen Streckung eines geraden Stabes der Länge L auf die Länge u+L

Die Gleichungen der Kontinuumsmechanik für Festkörper erfahren eine erhebliche Vereinfachung, wenn kleine Verschiebungen angenommen werden können. Verschiebungen sind die Differenz der Ortsvektoren Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{x}=\vec{\chi}(\vec{X},t)} eines Partikels Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{X}} in der Momentankonfiguration und seiner Ausgangslage Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{X}} :

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{u}=\vec{\chi}(\vec{X},t)-\vec{X} =: \left( \begin{array}{c} u(\vec{X},t)\\ v(\vec{X},t) \\ w(\vec{X},t) \end{array}\right)}

und der Verschiebungsgradient ist der Tensor

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{H}=\operatorname{GRAD}\;\vec{u}=\mathbf{F}-\mathbf{1} = \left(\begin{array}{ccc} \frac{\partial u}{\partial X} & \frac{\partial u}{\partial Y} & \frac{\partial u}{\partial Z} \\[1ex] \frac{\partial v}{\partial X} & \frac{\partial v}{\partial Y} & \frac{\partial v}{\partial Z} \\[1ex] \frac{\partial w}{\partial X} & \frac{\partial w}{\partial Y} & \frac{\partial w}{\partial Z} \end{array}\right) \,.}

Wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L_0} eine charakteristische Abmessung des Körpers ist, dann wird bei kleinen Verschiebungen sowohl Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left|\vec{u}\right| \ll L_0} als auch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \| \mathbf{H} \| \ll 1} gefordert, so dass alle Terme, die höhere Potenzen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{u}} oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{H}} beinhalten, vernachlässigt werden können. Bei kleinen Verschiebungen ist eine Unterscheidung der Lagrange’schen und Euler’schen Betrachtungsweise nicht mehr nötig, so dass die räumlichen Koordinaten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec x} und die materiellen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec X} nicht mehr auseinandergehalten werden müssen. Dies führt zu

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{F} = \mathbf{1}+\mathbf{H},\quad \mathbf{F}^{-1} \approx \mathbf{1}-\mathbf{H},\quad \det(\mathbf{F}) \approx 1+\operatorname{Sp}(\mathbf{H}),\quad \mathbf{E} \approx \mathbf{e} \approx \mathbf{E}_N \approx \mathbf{E}_H \approx \boldsymbol{\varepsilon} := \tfrac{1}{2}(\mathbf{H}+\mathbf{H}^\top) \,.}

Das bedeutet, dass alle aufgeführten Verzerrungsmaße bei kleinen Verschiebungen in den linearisierten Verzerrungstensor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \boldsymbol{\varepsilon}} übergehen. Der linearisierte Verzerrungstensor

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \boldsymbol{\varepsilon} = \tfrac{1}{2}(\mathbf{H}+\mathbf{H}^\top) = \left(\begin{array}{ccc} \frac{\partial u}{\partial x} & \frac{1}{2}\left(\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\right) & \frac{1}{2}\left(\frac{\partial u}{\partial z} + \frac{\partial w}{\partial x}\right) \\[1ex] \frac{1}{2}\left(\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\right) & \frac{\partial v}{\partial y} & \frac{1}{2}\left(\frac{\partial v}{\partial z} + \frac{\partial w}{\partial y}\right) \\[1ex] \frac{1}{2}\left(\frac{\partial u}{\partial z} + \frac{\partial w}{\partial x}\right) & \frac{1}{2}\left(\frac{\partial v}{\partial z} + \frac{\partial w}{\partial y}\right) & \frac{\partial w}{\partial z} \end{array}\right) }

wird auch Ingenieursdehnung genannt, denn bei vielen Anwendungen im technischen Bereich liegen kleine Dehnungen vor oder sie müssen aus sicherheitstechnischen Gründen klein gehalten werden. Diese geometrisch lineare Betrachtung ist für Werte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \| \mathbf{H} \|} bis 3–8 % zulässig, siehe Bild. Liegen keine kleinen Verschiebungen vor, wird von finiten oder großen Verschiebungen gesprochen.

Manchmal wird für die geometrische Linearisierung nur Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \| \mathbf{H} \| \ll 1} gefordert und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left|\vec{u}\right| \ll L_0} fallen gelassen, so dass große Translationen bei nur kleinen Drehungen und Dehnungen erlaubt sind. Dann muss nach wie vor zwischen der Lagrange’schen und Euler’schen Betrachtungsweise unterschieden werden.

Naturgesetze

Die in der Mechanik für ausgedehnte Körper formulierten Naturgesetze werden in der Kontinuumsmechanik als globale Integralgleichungen ausgedrückt, aus denen sich mit geeigneten Stetigkeitsannahmen lokale (Differential-)Gleichungen ableiten lassen, die an jedem materiellen Punkt erfüllt sein müssen. Mittels Äquivalenz-Umformungen der lokalen Gleichungen können anschließend weitere Prinzipien motiviert werden. Die globalen und lokalen Gleichungen können des Weiteren auf die räumlichen oder die materiellen Größen bezogen sein, so dass es für jedes Gesetz vier äquivalente Formulierungen gibt. Die hier verwendeten Formeln und weitere sind in der Formelsammlung Tensoranalysis zusammengefasst.

Die Bilanzgleichungen der Mechanik beschreiben die Wirkung der Außenwelt auf einen Körper und die daraus resultierende Änderung physikalischer Größen. Diese Größen sind die Masse, der Impuls, der Drehimpuls und die Energie. Neben den in der Mechanik bekannten äußeren Einflüssen gibt es im Kontinuum auch innere Quellen und Senken, z. B. ist die Schwerkraft eine innere Quelle für Spannungen. In abgeschlossenen Systemen, wo per definitionem eine Wechselwirkung mit der Außenwelt ausgeschlossen wird, werden aus den Bilanzgleichungen Erhaltungssätze. Der zweite Hauptsatz der Thermodynamik wird in Form der Clausius-Duhem-Ungleichung berücksichtigt.

Spannungstensoren

→ Hauptartikel: Spannungstensor

Schnittspannungen im ebenen Spannungszustand in Abhängigkeit von der Normalen an die Schnittfläche. Rot: Normale in x-Richtung, Blau: Normale in y-Richtung.

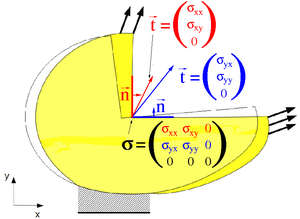
Grundlegend für die Formulierung der Bilanzgleichungen ist der Begriff des Spannungstensors, der die Spannungen in Körpern auf Grund äußerer Belastungen darstellt. Das zweite Newton’sche Gesetz beschreibt die Reaktion eines Körpers auf eine äußere Kraft. In der Realität und der Kontinuumsmechanik werden solche Kräfte immer flächig eingeleitet, d. h. auf einem Teil der Oberfläche des Körpers wirken Spannungsvektoren Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{t}} (Vektoren mit der Dimension Kraft pro Fläche) ein die sich in den Körper als Spannungen fortpflanzen. Nun kann der Körper gedanklich zerschnitten werden, so dass sich an den Schnittflächen Schnittspannungen ausbilden, die jedoch von der Orientierung der Schnittflächen, d. h. ihren Normalenvektoren, abhängen, siehe Abbildung rechts.

An einem freigeschnittenen (infinitesimal) kleinen Tetraeder sind die Volumenkräfte und die Impulsänderung als Terme dritter Ordnung gegenüber den oberflächig angreifenden Schnittspannungen, die Terme zweiter Ordnung in den Abmessungen des Tetraeders sind, vernachlässigbar klein. Aus dem Gleichgewicht am Tetraeder ergibt sich, dass der Zusammenhang zwischen der Normalen und den Spannungsvektoren linear sein muss, was der Inhalt des Cauchy’schen Fundamentaltheorems ist:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{t}=\boldsymbol{\sigma}^\top\cdot\vec{n}}

Der Cauchy’sche Spannungstensor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \boldsymbol{\sigma}} transformiert die Normale an die Schnittfläche Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{n}} in den Spannungsvektor. Bei der Übertragung dieses Zusammenhangs in die Lagrange’sche Betrachtungsweise muss noch die Veränderung der Flächenelemente berücksichtigt werden:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rcl} \vec{t}\,\mathrm{d}a &=& \boldsymbol{\sigma}^\top\cdot\vec{n}\,\mathrm{d}a = \boldsymbol{\sigma}^\top\cdot\det(\mathbf{F})\mathbf{F}^{\top-1} \cdot \vec{N}\,\mathrm{d}A =: \mathbf{N}^\top\cdot\vec{N}\,\mathrm{d}A =: \vec{t}_0 \,\mathrm{d}A \\ \Leftrightarrow \mathbf{N}&=&\det(\mathbf{F})\mathbf{F}^{-1}\cdot\boldsymbol{\sigma} \end{array} }

Der Spannungstensor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{N}} heißt Nominalspannungstensor und repräsentiert die Spannungen bezogen auf die Ausgangsfläche. Die transponierte des Nominalspannungstensors ist der erste Piola-Kirchhoff’sche Spannungstensor

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{P} := \mathbf{N}^\top\,.}

Später wird noch der zweite Piola-Kirchhoff’sche Spannungstensor

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{\mathbf{T}} :=\det(\mathbf{F}) \mathbf{F}^{-1} \cdot\boldsymbol{\sigma}\cdot\mathbf{F}^{\top-1} = \mathbf{N}\cdot\mathbf{F}^{\top-1} }

benötigt.

Bei kleinen Verzerrungen braucht nicht zwischen diesen Spannungstensoren unterschieden zu werden.

Massenbilanz

Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho (\vec{x},t)} die Dichte in der räumlichen und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho_0(\vec{X},t)} die in der materiellen Beschreibung. Unter der Annahme, dass es keine Massenquellen irgendeiner Form gibt, bedeutet die Massenbilanz, dass die Masse Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m} eines Körpers

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m=\int_v \rho \,\mathrm{d} v=\int_V \rho_0 \,\mathrm{d} V}

zeitlich konstant ist:

	Lagrange’sche Betrachtungsweise	Euler’sche Betrachtungsweise
globale Form	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}m =\frac{\mathrm{d}}{\mathrm{d}t} \int_V \rho_0 \,\mathrm{d} V=0}	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}m =\frac{\mathrm{d}}{\mathrm{d}t} \int_v \rho \,\mathrm{d} v=0}
lokale Form	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\dot{\rho}}_{0}=0}	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\partial}{\partial t}\rho +\operatorname{div}(\rho \vec{v}) = \underbrace{\frac{\partial \rho}{\partial t} + \operatorname{grad}(\rho)\cdot \vec{v}}_{ = \dot{\rho}} + \rho\,\operatorname{div}(\vec{v}) = \dot{\rho} + \rho \operatorname{div}(\vec{v}) =0}

Die lokalen Formen werden Kontinuitätsgleichung genannt. In der lokalen Euler’schen Formulierung wurde die Produktregel

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \operatorname{div}(\rho \vec{v}) = \operatorname{grad}(\rho)\cdot \vec{v} + \rho\,\operatorname{div}(\vec{v})}

und die materielle Zeitableitung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{\rho}} der Dichte eingesetzt.

Impulsbilanz

→ Hauptartikel: Erstes Cauchy-Euler’sches Bewegungsgesetz

Der Impulssatz besagt, dass die Änderung des Impulses gleich der von außen angreifenden Kräfte (volumenverteilt oder oberflächlich) ist:

	Lagrange’sche Betrachtungsweise	Euler’sche Betrachtungsweise
globale Form	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t} \int_V \rho_0 \dot{\vec{\chi}}\,\mathrm{d}V =\int_V \rho_0 \vec{k}_0 \,\mathrm{d}V+\int_A\vec{t}_0\,\mathrm{d}A}	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t} \int_v \rho \vec{v}\,\mathrm{d}v =\int_v \rho \vec{k}\,\mathrm{d}v+\int_a \vec{t}\,\mathrm{d}a}
lokale Form	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho_0 \ddot{\vec{\chi}} =\rho_0\vec{k}_0+\operatorname{DIV}\;\mathbf{N}}	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho \dot{\vec{v}} =\rho \dfrac{\partial}{\partial t}\vec{v}+\rho \operatorname{grad}(\vec{v})\cdot \vec{v} =\rho \vec{k}+\operatorname{div}\;\boldsymbol{\sigma}}

Der Vektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{k}_{(0)}} steht für eine Schwerebeschleunigung wie es die Schwerkraft eine ist, und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{t}_{(0)}} sind Oberflächenspannungen auf der Oberfläche Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A} bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} des Körpers zur Zeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t_0} bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} .

Drehimpulsbilanz

→ Hauptartikel: Zweites Cauchy-Euler’sches Bewegungsgesetz

Der Drehimpulssatz besagt, dass die Änderung des Drehimpulses gleich der von außen angreifenden Drehmomente (volumenverteilt oder oberflächlich) ist:

Lagrange’sche Betrachtungsweise

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t} \int_V (\vec{\chi}-\vec{c}){\times}\rho_0 \dot{\vec{\chi}}\,\mathrm{d}V =\int_V(\vec{\chi}-\vec{c}) \times \rho_0 \vec{k}_0\,\mathrm{d}V +\int_A (\vec{\chi}-\vec{c} ) \times \vec{t}_0\,\mathrm{d}A}

Euler’sche Betrachtungsweise

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t} \int_v (\vec{x}-\vec{c}){\times}\rho \vec{v}\,\mathrm{d}v =\int_v(\vec{x}-\vec{c}) \times \rho \vec{k}\,\mathrm{d}v +\int_a (\vec{x}-\vec{c} ) \times \vec{t}\,\mathrm{d}a}

Das Rechenzeichen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \times} bildet das Kreuzprodukt und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{c}} ist ein beliebiger, zeitlich fixierter Ortsvektor.

Die lokalen Formen reduzieren sich auf die Forderung nach der Symmetrie des zweiten Piola-Kirchhoff’schen und des Cauchy’schen Spannungstensors:

Lagrange’sche Betrachtungsweise	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{\mathbf{T}}=\tilde{\mathbf{T}}^\top}
Euler’sche Betrachtungsweise	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \boldsymbol{\sigma}=\boldsymbol{\sigma}^\top}

Energiebilanz

Die thermomechanische Energiebilanz besagt, dass die Änderung der Gesamtenergie eines Körpers gleich der Summe aus Wärmezufuhr und Leistung aller äußeren Kräfte ist. Die Gesamtenergie setzt sich in der Lagrange’schen Betrachtungsweise aus der inneren Energie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_V \rho_0 u_0\,\mathrm{d}V} mit der spezifischen inneren Energie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle u_0} und der kinetischen Energie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_V\frac{\rho_0}2\dot{\vec{\chi}}\cdot\dot{\vec{\chi}}\,\mathrm{d}V} zusammen:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t} \int_V \rho_0 u_0 \,\mathrm{d}V +\frac{\mathrm{d}}{\mathrm{d}t} \int_V \frac{\rho_0}2\dot{\vec{\chi}}\cdot\dot{\vec{\chi}}\,\mathrm{d}V =\int_V \rho_0 \vec{k}_0 \cdot\dot{\vec{\chi}}\,\mathrm{d}V +\int_A \vec{t}_0 \cdot \dot{\vec{\chi}}\,\mathrm{d}A +\int_V \rho_0 r_0 \,\mathrm{d}V -\int_A \vec{N}\cdot \vec{q}_0 \,\mathrm{d}A\,.}

Darin sind Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r_0} innere Wärmequellen des Körpers, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{q}_0} der Wärmestrom pro Fläche und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{N}} die auf dem Oberflächenelement Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{d} A} des Körpers nach außen gerichtete Normale. Das negative Vorzeichen des letztens Terms liefert eine Energiezufuhr, wenn der Wärmestrom in den Körper gerichtet ist.

In der Euler’schen Betrachtungsweise heißt die globale Energiebilanz:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t} \int_v \rho u\,\mathrm{d}v+\frac{\mathrm{d}}{\mathrm{d}t} \int_v \frac{\rho}2\vec{v} \cdot\vec{v}\,\mathrm{d}v=\int_v \rho \vec{k}\cdot\vec{v}\,\mathrm{d}v+\int_a \vec{t}\cdot\vec{v}\,\mathrm{d}a+\int_v \rho r \,\mathrm{d}v-\int_a \vec{n}\cdot\vec{q}\,\mathrm{d}a\,.}

Die lokalen Formen lauten:

Lagrange’sche Betrachtungsweise	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{u}_0=\frac{1}{\rho_0}\tilde{\mathbf{T}}:\dot{\mathbf{E}} -\frac{1}{\rho_0}\operatorname{DIV}\;\vec{q}_0+r_0}
Euler’sche Betrachtungsweise	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \dot{u}=\frac{1}{\rho}\boldsymbol{\sigma}:\mathbf{d} -\frac{1}{\rho}\operatorname{div}\;\vec{q}+r}

Prinzip von d’Alembert in der Lagrange’schen Fassung

→ Hauptartikel: d’Alembertsches Prinzip

Das Prinzip von d’Alembert in der Lagrange’schen Fassung (d. h. in materieller Darstellung) hat eine grundlegende Bedeutung für die Lösung von Anfangsrandwertaufgaben der Kontinuumsmechanik, insbesondere der Verschiebungsmethode in der Finite-Elemente-Methode. Das Prinzip von d’Alembert in der Lagrange’schen Fassung ist eine zur lokalen Impulsbilanz (in materieller Darstellung) äquivalente Aussage über Arbeiten von im System auftretenden Kräften und Spannungen an virtuellen Verschiebungen bzw. virtuellen Verzerrungen.

Unter der Verschiebung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{u}} eines materiellen Punktes in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{X}} wird der Differenzvektor von seiner momentanen Lage Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{x}=\vec{\chi}(\vec{X},t)} und seiner Ausgangslage Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{X}} verstanden: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{u}=\vec{x}-\vec{X}} . Virtuelle Verschiebungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta \vec{u}} sind von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{u}} unabhängige, gedachte, weitgehend beliebige, differenzielle Verschiebungen, die mit den geometrischen Bindungen des Körpers verträglich sind. Die virtuellen Verschiebungen müssen verschwinden, wo immer Verschiebungsrandbedingungen des Körpers vorgegeben sind. Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {A}^{u}} der Teil der Oberfläche Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A} des Körpers, auf dem Verschiebungsrandbedingungen erklärt sind. Für ein materielles Vektorfeld der virtuellen Verschiebungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta \vec{u}(\vec{X})} ist dann

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta \vec{u}(\vec{X})=\vec{0}{\quad\forall\;}\vec{X}{\in}{A}^{u}}

zu fordern. Auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {A}^{u}} können dann keine Oberflächenspannungen vorgegeben werden. Deshalb bezeichnet Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {A}^{\sigma}=A\setminus A^{u}} den Teil der Oberfläche des Körpers, auf dem Oberflächenspannungen wirken (können). Analog zu den auf den Verschiebungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{u}} basierenden Verzerrungen entwickeln sich virtuelle Verzerrungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta\mathbf{E}} aus den virtuellen Verschiebungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta\vec{u}} , weswegen diese mindestens einmal stetig differenzierbar sein sollen:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta\mathbf{E} := \frac{1}{2}( \mathbf{F}^\top \cdot \delta\mathbf{F} + \delta \mathbf{F}^\top \cdot \mathbf{F}) = \left.\frac{\mathrm{d}}{\mathrm{d}s} \mathbf{E}(\mathbf{F}+s\;\delta\mathbf{F})\right|_{s=0} \,.}

Darin ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta\mathbf{F}:=\operatorname{GRAD}(\delta \vec{u})} der virtuelle Deformationsgradient.

Indem die lokale Impulsbilanz in der Lagrange’schen Formulierung skalar mit den virtuellen Verschiebungen multipliziert und das Ergebnis über das Volumen des Körpers integriert wird, entsteht

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_{V} \delta \vec{u}\cdot( \rho_0\vec{k}_0 + \operatorname{DIV}\;\mathbf{N} - \rho_0 \ddot{\vec{\chi}})\, \mathrm{d}V = 0 \quad\forall\; \delta\vec{u} \in \mathcal{V} \,.}

Die Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathcal{V}} enthält alle zulässigen virtuellen Verschiebungen. Weil diese Gleichung für alle möglichen virtuellen Verschiebungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta \vec{u}\in\mathcal{V}} gilt, verschwindet das Volumenintegral stets nur genau dann, wenn der Term in den Klammern überall verschwindet. Dies wird auch „schwache Formulierung“ der Impulsbilanz genannt. Weitere Umformung der Integralgleichung durch Ausnutzung des Cauchy’schen Fundamentaltheorems, des Gauß’schen Integralsatzes, der Produktregeln für die Divergenz und der Symmetrie des zweiten Piola-Kirchhoff Spannungstensors führt auf das Prinzip von d’Alembert in der Lagrange’schen Fassung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_{V}\delta \vec{u}\cdot{\rho}_{0}\ddot{\vec{u}}\,\text{d}V + \int_{V}\tilde{\mathbf{T}}:\delta\mathbf{E}\,\text{d}V = \int_{{A}^{\sigma}}\delta \vec{u}\cdot\vec{t}_{0}\,\text{d}A + \int_{V}\delta \vec{u}\cdot \rho_{0}\vec{k}_0\,\text{d}V \quad\forall\; \delta\vec{u} \in \mathcal{V} \,.}

Auf der linken Seite steht die virtuelle Arbeit der Trägheitskräfte und die virtuelle Deformationsarbeit und auf der rechten Seite die virtuelle Arbeit der äußeren Kräfte (oberflächen- und volumenverteilt). Die genaue Herleitung ist in den Folgerungen aus den Cauchy-Euler’schen-Bewegungsgesetzen nachzuschlagen.

Clausius-Duhem-Ungleichung

→ Hauptartikel: Clausius-Duhem-Ungleichung

Die Clausius-Duhem-Ungleichung folgt aus der Anwendung des zweiten Hauptsatzes der Thermodynamik auf Festkörper. Mit den in quasi stationären Prozessen gerechtfertigten Annahmen der Entropieproduktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r/T} und des Entropieflusses Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{q}/T} leitet sich mit der spezifischen Entropie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s} aus dem zweiten Hauptsatz der Thermodynamik die Clausius-Duhem-Ungleichung ab:

	Lagrange’sche Betrachtungsweise	Euler’sche Betrachtungsweise
globale Form	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}\int_V s_0\, \rho_0\mathrm{d}V \ge \int_V \frac{r_0}{T}\, \rho_0\mathrm{d}V -\int_A\frac{\vec{q}_0}{T}\cdot\vec{N}\,\mathrm{d}A}	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t} \int_v s\, \rho\mathrm{d}V \ge \int_v \frac{r}{T}\,\rho\mathrm{d}v -\int_a \frac{\vec{q}}{T}\cdot\vec{n}\,\mathrm{d}a}
lokale Form	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{\rho_0}\tilde{\mathbf{T}}:\dot{\mathbf{E}} -\dot{\psi}_0 - s_0\dot{T}_0 -\frac{\vec{q}_0}{\rho_0 T_0}\cdot\operatorname{GRAD}\;T_0\ge 0}	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{\rho}\boldsymbol{\sigma}:\mathbf{d} - \dot{\psi}-s\dot{T} -\frac{\vec{q}}{\rho T}\cdot\operatorname{grad}\;T\ge 0}

Hier ist wieder das negative Vorzeichen des letzten Terms in den globalen Formen der nach außen gerichteten Normalen geschuldet, siehe #Energiebilanz oben. Die Helmholtz’sche freie Energie:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \psi = u - s T \quad\rightarrow\quad \dot{\psi} + s \dot{T} = \dot{u} - \dot{s} T }

ersetzt in den lokalen Formen die innere Energie. Im wichtigen Sonderfall, in dem Temperaturänderungen vernachlässigt werden können, vereinfachen sich die lokalen Formen zu:

	Lagrange’sche Betrachtungsweise	Euler’sche Betrachtungsweise
lokale Form	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{\rho_0}\tilde{\mathbf{T}}:\dot{\mathbf{E}}-\dot{\psi}_0\ge 0}	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{\rho}\boldsymbol{\sigma}:\mathbf{d}-\dot{\psi}\ge 0}

Das Skalarprodukt der Spannungen mit den Verzerrungsgeschwindigkeiten ist die spezifische Spannungsleistung und derjenige Anteil von ihr, der über die Produktion an freier Energie hinaus geht, wird dissipiert. Die lokalen Formen der Clausius-Duhem-Ungleichung sind weniger als Einschränkung physikalischer Prozesse, sondern vielmehr als Anforderung an Materialmodelle zu interpretieren: Es muss sichergestellt sein, dass die lokalen Formen der Clausius-Duhem-Ungleichung von den konstitutiven Gleichungen für beliebige Prozesse erfüllt werden.

Materialtheorie

Die Materialtheorie beschäftigt sich mit den individuellen Merkmalen von Materialien und der Erstellung mathematischer Modelle hiervon. Ziel eines Materialmodells ist es, die wesentlichen Aspekte des Materialverhaltens zu beschreiben, wobei das was wesentlich ist, vom Beobachter festgelegt wird. Stoff- oder Materialgesetze, wie Materialmodelle manchmal genannt werden, haben nicht die allgemeine Gültigkeit physikalischer Gesetze. Zentral in der Materialmodellierung ist die Abhängigkeit der Spannungen von den Dehnungen (oder umgekehrt) in Form von Gleichungen zu beschreiben, so dass die Deformation von Körpern aus diesem Material berechnet werden kann. Die klassische Kontinuumsmechanik betrachtet einfache Materialien, deren Eigenschaften mit materiellen Zwangsbedingungen, materiellen Symmetrien und konstitutiven Gleichungen wiedergegeben werden.

Einfache Materialien

Die Materialtheorie der klassischen Kontinuumsmechanik setzt Determinismus, Lokalität und Objektivität des Materials voraus. Determinismus bedeutet, dass der aktuelle Zustand eines Körpers in einem seiner materiellen Punkte vollständig und eindeutig durch die vergangene Bewegung des Körpers bestimmt wird. Lokalität schränkt die Einflusssphäre der Außenwelt auf den aktuellen Spannungszustand in einem materiellen Punkt auf seine nahe Umgebung ein, Wirkungen pflanzen sich von einem materiellen Punkt zu seinen nächsten fort. Materielle Objektivität bedeutet, dass die Materialantwort vom Bezugssystem des Beobachters unabhängig ist, siehe Euklidische Transformation. Materialien, die diese drei Voraussetzungen erfüllen, heißen einfach. Bei einfachen Materialien vom Grad eins ergeben sich die Spannungen in einem materiellen Punkt aus den vergangenen Werten und dem aktuellen Wert des Green-Lagrange’schen Verzerrungstensors oder daraus ableitbaren Größen in diesem Punkt. Materialien höheren Grades benutzen auch höhere Ableitungen nach den materiellen Koordinaten als die ersten, die den Deformationsgradienten ausmachen.

Materielle Zwangsbedingungen

Materielle Zwangsbedingungen stellen kinematische Nebenbedingungen dar, die die Deformationsmöglichkeiten eines Materials einschränken. Die bekannteste dieser Bedingungen ist die Inkompressibilität, die dem Material nur volumenerhaltende Verformungen erlauben, wie sie einige Flüssigkeiten oder gummielastische Materialien zeigen. Die kinematische Nebenbedingung lautet hier Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \det(\mathbf{F})\equiv 1} . Die Reaktionsspannungen im Material ergeben sich dann nicht mehr aus den Konstitutivgleichungen, sondern aus den Bilanzgleichungen und Randbedingungen. Bei Inkompressibilität z. B. ist die Reaktionsspannung der Druck im Material. Die stärkste Nebenbedingung ist die, die den starren Körper auszeichnet. Hier entfallen alle Konstitutivgleichungen und die Spannungen sind vollständig durch die Naturgesetze und Randbedingungen bestimmt.

Materielle Symmetrien

Materielle Symmetrien beschreiben welche Transformationen des Materials möglich sind, ohne dass sich bei gegebenem Deformationsgradient die Spannungen ändern. Diese Transformationen bilden die Symmetriegruppe des Materials. Sind alle volumenerhaltenden Transformationen erlaubt, liegt eine Flüssigkeit oder ein Gas vor. Bei Feststoffen sind nur Drehungen möglich: Bei isotropen Feststoffen sind alle Drehungen, bei transversal isotropen beliebige Drehungen um eine Achse, bei kubisch anisotropen nur 90-Grad-Drehungen um drei zueinander orthogonale Achsen, bei orthotropen nur 180-Grad-Drehungen um drei zueinander orthogonale Achsen und bei vollständig anisotropen sind nur "Drehungen" um 0 Grad erlaubt.

Konstitutive Gleichungen

Die konstitutiven Gleichungen geben eine Relation zwischen den Dehnungen und den Spannungen in Form von Integral-, Differential- oder algebraischen Gleichungen. Die folgenden Materialmodelle geben Beispiele für konstitutive Gleichungen.

1. Ideales Gas: Beim idealen Gas ist der Druck Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p} proportional zur Dichte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho} und Temperatur Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T} :
   Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \boldsymbol{\sigma} =-p\mathbf{1}=-RT\rho \mathbf{1}}
   Die Zahl Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R} ist ein Materialparameter. Dieses Materialmodell führt in Verbindung mit der Kontinuitätsgleichung und der Impulsbilanz auf die Euler-Gleichungen.
2. Linear viskoses oder newtonsches Fluid:
   Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \boldsymbol{\sigma} =-p(\rho )\mathbf{1}+2\mu \mathbf{d}+\lambda \operatorname{Sp}(\mathbf{d})\mathbf{1}}
   Die Materialparameter Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu} sind die ersten und zweiten Lamé-Konstanten und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \operatorname{Sp}} die Spur. Dieses Materialmodell liefert in Verbindung mit der Kontinuitätsgleichung und der Impulsbilanz die Navier-Stokes-Gleichungen.
3. Hookesches Gesetz für linear elastische isotrope Festkörper:
   Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \boldsymbol{\sigma} =2G\left(\boldsymbol{\varepsilon}+\frac{\nu}{1-2\nu} \operatorname{Sp}(\boldsymbol{\varepsilon} )\mathbf{1}\right)} .
   Es ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle G} der Schubmodul, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu} die Querkontraktionszahl. Dieses Materialmodell ergibt in Verbindung mit der Impulsbilanz die Navier-Cauchy-Gleichungen.
4. Viskoelastizität:
   Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \boldsymbol{\sigma}=2\int_0^t \gamma(t-\tau )\boldsymbol{\varepsilon}(\tau )'^\mathrm{D}\,\mathrm{d}\tau +\int_0^t \kappa (t-\tau )\operatorname{Sp}[ \boldsymbol{\varepsilon}(\tau )\text{'}] \,\mathrm{d}\tau \mathbf I} .
   Es bedeutet Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (\cdot)'} die Ableitung nach dem Zeitparameter Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tau} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (\cdot)^\mathrm{D}} den Deviator und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma (t)} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa (t)} sind Relaxationsfunktionen für den Schub- bzw. den volumetrischen Anteil der Deformation.
5. Plastizität: Bei der geschwindigkeitsunabhängigen Plastizität wird das Materialverhalten mit algebraischen und Differentialgleichungen beschrieben. Die algebraischen Gleichungen legen die additive Aufspaltung der Dehnungen in einen elastischen und einen plastischen Anteil, die Beziehung zwischen den Spannungen und den elastischen Dehnungen sowie die Fließfläche fest, die im Spannungsraum den elastischen Bereich vom plastischen Bereich trennt. Mit Differentialgleichungen wird die Entwicklung der inneren Variablen, z. B. der plastischen Dehnungen, beschrieben. In der klassischen Plastizität bleiben die Spannungen beim Fließen auf der Fließfläche.
6. Viskoplastizität: Bei der geschwindigkeitsabhängigen Plastizität wird das Materialverhalten auch mit algebraischen und Differentialgleichungen dargestellt. Hier können die Spannungen jedoch zeitweilig außerhalb der Fließfläche liegen, kehren aber bei einer Relaxation auf diese zurück.

Die Feststoffmodelle drei bis sechs sind Repräsentanten der vier Gruppen von Modellen der klassischen Materialtheorie, die geschwindigkeitsabhängiges oder unabhängiges Verhalten mit oder ohne (Gleichgewichts-)Hysterese beschreiben.

Beispiel

Drehung mit uniaxialer Verformung. Die Ausgangskonfiguration ist in grau, die Momentankonfiguration in grün dargestellt.

Anhand der Dehnung eines verdrehten Klotzes unter reinem Zug (siehe Bild) sollen die Gleichungen der Kontinuumsmechanik angewendet werden. Er habe in der Ausgangskonfiguration im globalen kartesischen Koordinatensystem die Länge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L} in x-Richtung, die Breite Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B} in y-Richtung und Höhe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H} in z-Richtung und sei im Ursprung parallel zu den Koordinatenachsen ausgerichtet. Dieser Klotz werde langgezogen, wobei sich Streckungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda ,\beta ,\eta} in materieller X-, Y- bzw. Z-Richtung einstellen, und anschließend um 90° um die z-Achse gedreht.

In der Momentankonfiguration haben die materiellen Punkte

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{X}=(X,Y,Z)^\top \in [0,L]\times [0,B] \times [0,H]}

dann die räumlichen Koordinaten

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{\chi}(\vec{X},t) =\begin{pmatrix}x \\ y \\ z \end{pmatrix} =\begin{pmatrix} -\beta Y \\ \lambda X \\ \eta Z\end{pmatrix}\,.}

Die materiellen Linien mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X \in [0,L]} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y,Z=\mathrm{const.}} sind in der Momentankonfiguration also parallel zur y-Achse ausgerichtet. In der Momentankonfiguration entspricht ein Zug in materieller x-Richtung einem Zug in räumlicher y-Richtung.

Der Deformations- und Verschiebungsgradient berechnen sich aus der Ableitung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{F}=\sum_{i,j=1}^3 \frac{\mathrm{d}\chi_i}{\mathrm{d} X_j}\vec{e}_i \otimes \vec{e}_j =\begin{pmatrix} 0 & -\beta & 0 \\ \lambda & 0 & 0 \\ 0 & 0 & \eta \end{pmatrix} \Rightarrow \mathbf{H}=\begin{pmatrix} -1& -\beta & 0\\ \lambda & -1& 0\\ 0& 0& \eta -1 \end{pmatrix}\,.}

Wegen der Drehung um 90° ergibt sich die polare Zerlegung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l} \mathbf{F} = \begin{pmatrix} 0& -\beta & 0\\ \lambda & 0& 0\\ 0& 0& \eta \end{pmatrix}=\begin{pmatrix} 0& -1& 0\\ 1& 0& 0\\ 0& 0& 1 \end{pmatrix} \begin{pmatrix} \lambda & 0& 0\\ 0& \beta & 0\\ 0& 0& \eta \end{pmatrix} = \begin{pmatrix} \beta & 0& 0\\ 0& \lambda & 0\\ 0& 0& \eta \end{pmatrix} \begin{pmatrix} 0& -1& 0\\ 1& 0& 0\\ 0& 0& 1 \end{pmatrix} \\ \Rightarrow \mathbf{R} = \begin{pmatrix} 0& -1& 0\\ 1& 0& 0\\ 0& 0& 1 \end{pmatrix}, \mathbf{U} = \begin{pmatrix} \lambda & 0& 0\\ 0& \beta & 0\\ 0& 0& \eta \end{pmatrix}, \mathbf{V} = \begin{pmatrix} \beta & 0& 0\\ 0& \lambda & 0\\ 0& 0& \eta \end{pmatrix} \end{array}\,.}

Daraus bekommt man die Verzerrungstensoren:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l} \mathbf{E}=\frac{1}{2}\begin{pmatrix} \lambda^2-1& 0& 0\\ 0& {\beta}^2-1& 0\\ 0& 0& {\eta}^2-1\end{pmatrix}, \mathbf{e}=\frac{1}{2}\begin{pmatrix} 1-{\beta}^{-2}& 0& 0\\ 0& 1-\lambda^{-2}& 0\\ 0& 0& 1-{\eta}^{-2} \end{pmatrix}, \\ {\mathbf{E}}_{N}=\begin{pmatrix} \lambda -1& 0& 0\\ 0& \beta -1& 0\\ 0& 0& \eta -1 \end{pmatrix},\mathbf{E}_H =\begin{pmatrix} \ln (\lambda )& 0& 0\\ 0& \ln (\beta )& 0\\ 0& 0& \ln (\eta ) \end{pmatrix} \\ \boldsymbol{\varepsilon}=\frac{1}{2}\begin{pmatrix} -2& \lambda -\beta & 0\\ \lambda -\beta & -2& 0\\ 0& 0& 2\eta -2 \end{pmatrix} \end{array}}

woran man sieht, dass bei großen Drehungen die geometrisch linearen Dehnungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \boldsymbol{\varepsilon}} nicht benutzbar sind.

Unter Verwendung des Hooke’schen Gesetzes bei großen Deformationen ergeben sich die zweiten Piola Kirchhoff Spannungen im Lagrange’schen Bild:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{\mathbf{T}} = 2G\left[\mathbf{E}+\frac{\nu}{1-2\nu}\operatorname{Sp}(\mathbf{E})\mathbf{1}\right] =2G\left[\frac{1}{2} \begin{pmatrix} \lambda^2-1& 0& 0\\ 0& {\beta}^2-1& 0\\ 0& 0& {\eta}^2-1 \end{pmatrix} + \frac{\nu (\lambda^2+\beta^2+\eta^2-3)}{2(1-2\nu )} \begin{pmatrix} 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1 \end{pmatrix} \right]\,.}

Bei reinem Zug in materieller x-Richtung mittels Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{\mathbf{T}}=\tilde{T}_{xx} \vec{e}_x\otimes\vec{e}_x} erkennt man Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta =\eta} und daher

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{2}(\beta^2-1)+\frac{\nu (\lambda^2+2\beta^2-3)}{2(1-2\nu )} =0 \Rightarrow \frac{\beta^2-1}2=\frac{\eta^2-1}2=-\nu \frac{\lambda^2-1}2 \Rightarrow \tilde{T}_{xx}=\mathrm{E}\frac{\lambda^2-1}2\,,}

worin Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{E}=2G(1+\nu )} der Elastizitätsmodul ist. Der Nominalspannungstensor lautet

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{N}=\tilde{\mathbf{T}}\cdot\mathbf{F}^\top = \begin{pmatrix} \tilde{T}_{xx} & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}\cdot \begin{pmatrix} 0 & \lambda & 0 \\ -\beta & 0 & 0 \\ 0 & 0 & \eta \end{pmatrix} = \begin{pmatrix} 0 & N_{xy} & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_{xy} =\mathrm{E}\lambda \frac{\lambda^2-1}{2}\,.}

In der hier betrachteten Statik besagt der Impulssatz

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{0}=\operatorname{DIV}\;\mathbf{N} =\frac{\partial}{\partial X} N_{xy}\vec{e}_y\,,}

was wegen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda=\mathrm{const.}} gegeben ist. Der Cauchy’sche Spannungstensor bekommt die Form:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \boldsymbol{\sigma} =\frac{\mathbf{F\cdot N}}{\det(\mathbf{F})} = \frac{1}{\lambda\beta\eta} \begin{pmatrix} 0& -\beta & 0\\ \lambda & 0& 0\\ 0& 0& \eta \end{pmatrix}\cdot \begin{pmatrix} 0 & N_{xy} & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} =\mathrm{E}\frac{\lambda (\lambda^2-1)}{2(1+\nu -\nu \lambda^2)} \vec{e}_y\otimes\vec{e}_y\,.}

Drückt man den Klotz auf null Länge zusammen, so dass Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda=0} ist, verschwinden diese Spannungen. Dies zeigt, dass das Hooke’sche Gesetz bei derart großen Verformungen nicht anwendbar ist. Das Hooke’sche Gesetz ergibt nur bei moderaten Dehnungen physikalisch plausible Antworten.

Als Referenzkonfiguration Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{\Theta}=\kappa_R (P)} eignet sich der Einheitswürfel

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (\Theta_1,\Theta_2,\Theta_3)\in {[ -1,1]}^3\subset\mathbb{V}^3\,.}

So bekommen die materiellen Punkte in der Ausgangskonfiguration Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{X}=\kappa_0(\kappa_{R}^{-1}(\vec{\Theta}))=:\vec{\chi}_{0}(\vec{\Theta})} die Koordinaten

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X=\tfrac{1}{2} L(\Theta_1+1),\quad Y =\tfrac{1}{2} B(\Theta_2+1),\quad Z=\tfrac{1}{2} H(\Theta_3+1)\,.}

Der zwischen der Referenz- und der Ausgangskonfiguration operierende "Deformationsgradient" wird auch als Jacobi-Matrix bezeichnet:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf{J}(\vec{\Theta}) =\sum_{i,j=1}^3\frac{\mathrm{d} \chi_{0i}}{\mathrm{d} \Theta_j} \vec{e}_i \otimes \vec{e}_j =\frac{1}{2}\begin{pmatrix} L& 0& 0\\ 0& B& 0\\ 0& 0& H \end{pmatrix} \quad\rightarrow\quad \det(\mathbf{J})=\frac{LBH}{8} \,.}

Das Volumenintegral einer Feldgröße Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \phi} lautet dann

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_{V}\phi(\vec{X},t)\mathrm{d}V = \int_{-1}^1 \int_{-1}^1 \int_{-1}^1 \phi(\chi_0 (\vec{\Theta}),t) \det(\mathbf{J}(\vec{\Theta}))\, \mathrm{d}\Theta_1\,\mathrm{d}\Theta_2\,\mathrm{d} \Theta_3 }

und kann in dieser Form numerisch mit der Gauß-Quadratur berechnet werden.

Siehe auch

• Technische Mechanik, Rheologie
• Cauchy-Elastizität, Hyperelastizität, Hypo-Elastizität
• Orthotropie, Transversale Isotropie, Kubische Anisotropie
• Hauptinvariante
• Spannungsfunktion, Airysche Spannungsfunktion
• Kompatibilitätsbedingung
• Orthogonaler Tensor, Deviator, Kugeltensor

Literatur

• H. Altenbach: Kontinuumsmechanik. Springer Verlag, 2012, ISBN 978-3-642-24118-5.
• H. Parisch: Festkörper Kontinuumsmechanik. Teubner, 2003, ISBN 3-519-00434-8.
• A. Bertram: Axiomatische Einführung in die Kontinuumsmechanik. Wissenschaftsverlag, 1989, ISBN 3-411-14031-3.
• Ernst Becker & Wolfgang Bürger: Kontinuumsmechanik. Teubner, 1975, 228 S., ISBN 3-519-02319-9.
• F. Durst: Grundlagen der Strömungsmechanik. Springer Verlag, 2006, ISBN 3-540-31323-0.
• Ralf Greve: Kontinuumsmechanik. Springer Verlag, 2003, ISBN 3-540-00760-1.
• Peter Haupt: Continuum Mechanics and Theory of Materials. Springer, Berlin u. a. 2000, ISBN 3-540-66114-X.
• Wolfgang H. Müller: Streifzüge durch die Kontinuumstheorie. Springer Verlag, 2011, ISBN 3-642-19869-4
• Valentin L. Popov: Kontaktmechanik und Reibung. Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation. Springer Verlag, 2009, ISBN 978-3-540-88836-9.
• Arnold Sommerfeld: Mechanik der deformierbaren Medien. (= Vorlesungen über theoretische Physik, Band 2). Becker & Erler, Leipzig 1945. (6. Auflage, Harri Deutsch, Thun 1992, ISBN 3-87144-375-1.)
• C. Truesdell, W. Noll: The non-linear field theories of mechanics. Springer Verlag, 1992, ISBN 3-540-55098-4.

Weblinks

Wiktionary: Kontinuumsmechanik – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Online-Vorlesung zur Kontinuumsphysik von Krishna Garikipati, University of Michigan (englisch)